矩阵式中频电源预测控制策略研究

胡风革，吴旭升，聂子玲，王 清

（1.海军工程大学舰船综合电力技术国防重点实验室，武汉 430033；2.邢台职业技术学院电气工程系，邢台054000）

现有大型舰船的飞机服务系统、航空航天及通信交换系统需要供电系统提供大容量、高可靠性的400 Hz中频交流电源[1]。基于常规逆变器拓扑结构的中频电源由于采用了直流支撑电容，存在体积大、可靠性不高和维修性差的缺点[2]。随着电力电子技术的发展，一种新型的拓扑结构——矩阵变换器引起学者们的极大关注[3-4]。矩阵变换器是一种不采用直流环节的直接型交交变频装置，具有正弦输入输出波形、功率因数可控、高功率密度、高可靠性等优点，在中频电源系统的应用中具有明显优势。

衡量中频电源性能的一个重要指标是输出电压波形质量及其动态响应性能。目前，国内外学者对矩阵式中频电源的波形质量控制技术进行了相关的研究，提出了基于空间矢量调制的闭环控制策略，其中包括比例积分控制[5]和重复控制[6]。PI控制存在静差，且不能同时满足稳态精度和动态响应的要求；基于内模原理的重复控制技术，可以补偿负载扰动获得理想的输出电压波形[7]，但其产生的一个周期延迟会降低系统的动态性能，无法满足高性能中频电源系统的动态指标要求。

预测控制是一种基于模型、滚动实施并结合反馈校正的优化控制算法，具有建模直观、动态响应快、无需脉宽调制，可灵活处理系统约束等优点[8-10]，在保证输出性能的同时可以实现对输入侧的控制，非常适用于矩阵式中频电源系统。本文采用了一种多步预测控制算法，对预测控制在矩阵式中频电源中的应用做了详细的分析。在此基础上，建立了矩阵式中频电源的预测模型，构建了满足控制目标的评价函数，实现了对中频电源的输入输出预测控制，实验结果验证了本文所设计矩阵式中频电源预测控制方法的正确性和有效性。

1 矩阵式中频电源数学模型

图1为三相矩阵式中频电源拓扑结构。图中SAa～SCc为双向可关断半导体开关器件，每个开关由2个共发射极的IGBT反串联构成。该电源采用三相工频输入，输入侧滤波器用于滤除网侧输入电流中的高频谐波分量，输出侧通过三相LC滤波电路向负载提供400 Hz输出电压，输入与输出通过双向开关直接连接，不含有直流储能环节。

图1 矩阵式中频电源拓扑结构Fig.1 Topology of matrix-converter-based medium frequency power supply

1.1 矩阵变换器开关模型

三相矩阵变换器包含9个双向开关，为满足输入不短路和输出不开路的要求，矩阵变换器共有27种有效的开关状态组合。开关状态约束条件为

相对于中性点N，矩阵变换器的输入输出电压之间的关系可表示为

式中：T为瞬态转移矩阵；vo和vi分别为矩阵变换器的输出和输入电压矢量；uA和ua分别为输出A相相电压和输入a相相电压。

由基尔霍夫电流定律，输入输出电流的关系为

式中：ii和io分别为矩阵变换器输入和输出电流空间矢量；iA和ia分别为输出A相相电流和输入a相相电流。

1.2 输入输出滤波器数学模型

输入、输出LC滤波器的数学模型分别为

式中：Li、Ci和Ri分别为输入滤波器的电感、电容和等效电阻；Lo、Co和Ro分别为输出滤波器的电感、电容和等效电阻为负载电流矢量；vL为三相输出滤波电容电压矢量；vs为电源电压矢量；is为电源输出电流矢量。

2 多步预测控制策略分析

预测控制算法依据系统预测模型，在1个控制周期内遍历控制对象所有开关状态下的系统输出，从中选择设计满足控制目标评价函数最小的开关状态，以此作用于控制对象，实现对目标的控制。

预测控制原理如图2所示。预测控制执行过程[12]如下：假设tk时刻，作用于控制对象的开关状态为S（tk），根据对象的预测模型 fp{x（tk），S（tk）}，计算出系统在 tk+1时刻的输出变量 xp（tk+1）；重复执行预测计算，可得到不同开关状态下的n个系统输出xpi（tk+2），最后结合依据控制目标所设计的评价函数，选择使得评价函数最小化的开关状态 S（tk+1），并在tk+1时刻作用于控制对象。

图2 预测控制原理Fig.2 Principle of predictive control

由上述分析可知，该方法是以输出量tk+1时刻的预测值为基础，结合评价函数，通过遍历法确定最优的开关状态S（tk+1）。其缺点是，没有考虑多个周期内的最优性，忽略了其他开关状态中潜在的最优性能。预测控制收敛性分析如图3所示，当系统中存在干扰或建模有误差时，随着误差的积累，会导致预测控制的结果出现振荡或发散。

为克服上述不足，本文借鉴文献[11]的思路，采用了多步预测控制算法。该算法的执行步骤如下。

图3 预测控制收敛性分析Fig.3 Convergence analysis of predictive control

步骤 1根据系统tk时刻的状态，由预测模型fp{x（tk），S（tk）}，计算系统预测值xp（tk+1）。

步骤 2根据x（tk+1），调用预测模型，得到所有开关状态下的预测值 xpi（tk+2），i=1，2，…，n；求解评价函数 g{x*，xpi（tk+2）}，从中选择使函数取最小值和次小值的预测值xpmin1（tk+2）和xpmin2（tk+2），其对应的开关状态为 xmin1（tk+1）和 xmin2（tk+1）。

步骤 3在 xpmin1（tk+2）和 xpmin2（tk+2）的基础上，2次调用预测模型，计算得到2n个tk+3时刻的预测值xpmin1i（tk+3）和 xpmin2i（tk+3）；求解评价函数 g{x*，xpji（tk+3）}，j=min1，min2，i=1，2，…，n，从中选择使g最小的预测值 xpmin1i（tk+3）或者xpmin2i（tk+3），i∈{1，2，…，n}，将对应的开关状态 Smin1（tk+1）或 Smin2（tk+1）在 tk+1时刻作用于系统。

多步预测控制原理如图4所示，在多步预测控制下，最优的开关状态应该是Smin2（tk+1），不同于传统预测控制算法得到的结果Smin1（tk+1）。

图4 多步预测控制原理Fig.4 Principle of multi-step predictive control

3 矩阵式中频电源的预测控制

中频电源的控制目标是三相负载电压准确跟踪参考电压，此外为了提高输入电源利用率，控制输入端无功功率为0。

3.1 中频电源预测模型

选取状态变量X=（vi，is）T，输入量u=（vs，i）T，由式（4）可得输入滤波器的状态方程为

将式（6）离散化后，可得

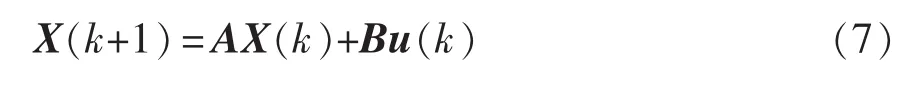
因此可得输入侧电源电流预测模型为

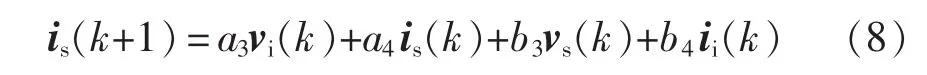
式中：vs（k），vi（k），is（k）可通过测量得到，ii（k）可由开关模型计算得到。

根据输入无功功率的计算公式，可得输入侧预测模型为

式中：Vsα、Vsβ表示电源电压矢量在αβ坐标系下的分量；isα、isβ表示输入电流矢量αβ坐标系下的分量。由于输入电源频率远小于系统采样频率，故vs（k+1）≈vs（k）。

同理，由输出侧滤波器的微分方程式（5），可得其状态方程为式中

将式（10）离散化，可得

由此，可得负载电压的预测模型为

其中，vL（k+1），io（k）可通过测量得到，vo（k）可根据开关模型计算得到可由测量的输出电流和负载电压计算得到，即

3.2 评价函数

结合所提出的输入输出控制目标，推导评价函数g的构造方法如下：

（1）将负载电压预测值vL（k+1）与v*L（k）给定值相减，可得电压差值ΔvL（k+1）为分别为负载电压给定值的 α、β分量。

（2）将输入侧无功功率预测值Qp（k+1）与给定值（0）相减，可得

（3）将ΔvL（k+1）和ΔQp（k+1）求加权平方和，可得该评价函数g为

式中，λ为加权系数，λ=0.006。

3.3 多步预测控制策略

矩阵式中频电源多步预测控制策略如图5所示。该方法选择开关状态的步骤如下：

步骤1测量tk时刻的输入量，计算tk+1时刻无功功率和负载电压的预测值，结合矩阵变换器27个有效开关矢量，得到tk+2时刻被控量的预测输出xi（k+2）i=1～27。

式中：vLα（k+1）和vLβ（k+1）分别为负载在αβ坐标系下的分量

图5 矩阵式中频电源多步预测控制策略Fig.5 Multi-step predictive control strategy for matrixconverter-based medium-frequency power supply

步骤2由评价函数选择与被控量参考值最接近和次接近的预测值，记为xmin1（k+2）和xmin2（k+2），对应的开关状态为Smin1（k+1）、Smin2（k+1）。

步骤3在第2步被控量预测值的基础上，分别调用预测模型，计算tk+3时刻被控量的预测输出xmin1i（k+3）和xmin2i（k+3）。根据评价函数，从54个输出量中选择与参考值最接近的预测值所对应的xmin1（k+2）或xmin2（k+2）。

步骤4由此，可确定tk+1时刻将要实施的最优开关状态Smin1（k+1）或者Smin2（k+2）。

4 实验结果

本文以DSP+FPGA为控制核心，采用英飞凌FZ400R12KE4为功率器件构建了一台矩阵式中频电源样机系统，如图6所示。实验参数为：工频交流电输入380 V/50 Hz，输入端接三相LC滤波器（Li=2 mH，Ci=10 μF，ri=0.5 Ω），用于滤除输入电流中的高频谐波分量，输出三相LC滤波器参数为（Lo=3 mH，Co=40 μF，ro=0.2 Ω）。参考输出电压115 V/400 Hz。

图7和图8所示分别为矩阵式中频电源在阻感负载和整流负载条件下的实验波形。由图7（a）可见，电源输入侧电压电流保持相位相同，输入侧的无功功率为0，与控制目标相一致；从图7（b）、（c）可见，控制输出电压的跟踪精度高，波形正弦性好，THD仅为1.57%。由图8可见，非线性负载下输出电压的THD为2.95%，验证了所提方法良好的稳态控制性能。

图6 矩阵式中频电源样机系统Fig.6 Prototype of matrix-converter-based mediumfrequency power supply

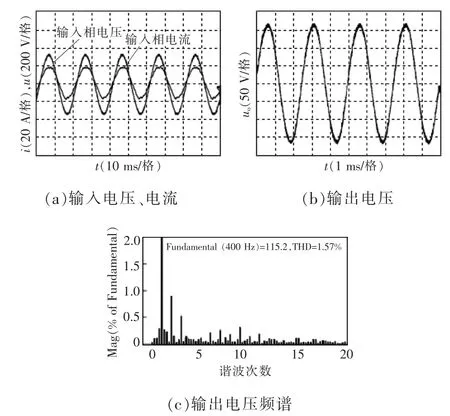
图7 阻感负载时电源实验波形Fig.7 Experimental waveforms with a resistive-inductive load

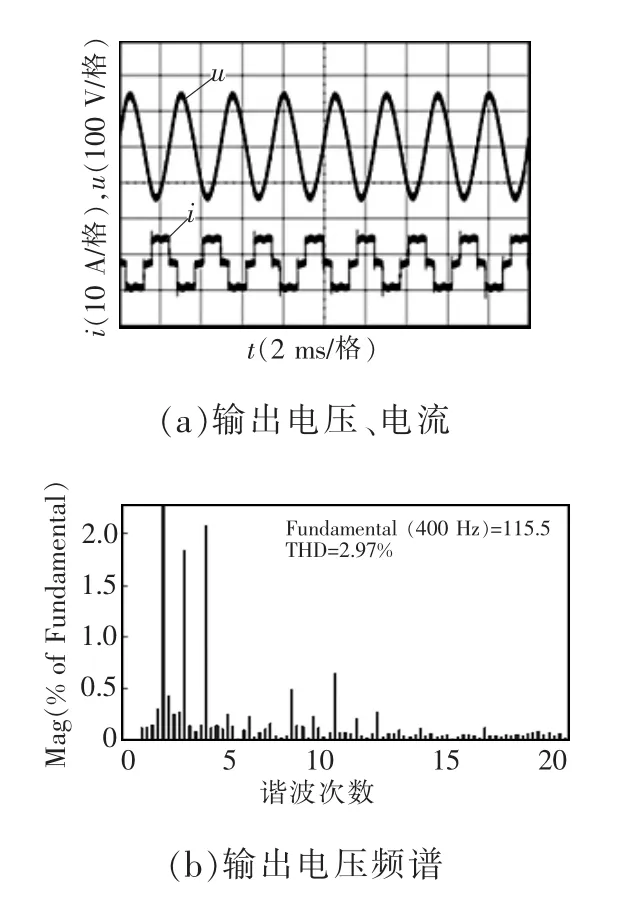
图8 整流负载时电源的实验结果Fig.8 Experimental results of power supply with a nonlinear load

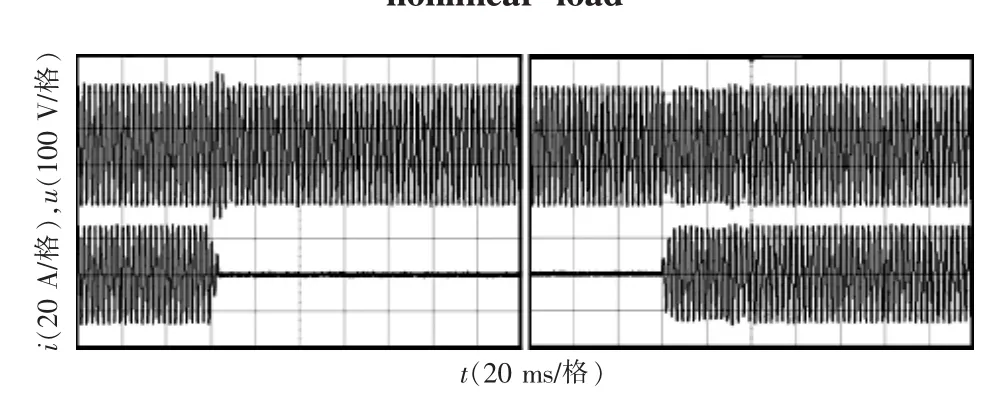
图9 突卸、突加负载时电源输出电压和电流波形Fig.9 Waveforms of output voltage and current from the power supply with a sudden load/unload

图9所示为样机在1 s内突加、突卸负载的输出电压和电流的实验波形。从图中可以看出，输出电压为115 V，电流为24 A，其动态恢复时间小于20 ms，证明了多步预测控制良好的动态响应。

5 结语

本文详细分析了预测控制算法的特性，采用了一种基于多步的预测方法。在此基础上，设计了矩阵式中频电源的预测控制算法，实验结果表明，所提控制方法具有良好的动、静态性能。在实现输出电压低谐波畸变的同时，控制电源系统输入侧无功功率为0，有效地提高了系统的运行效率。

[1]朱俊杰,马伟明,聂子玲.一种用于静止式中频电源的比例谐振控制策略[J].电机与控制学报,2012,16（10）：79-85.

Zhu Junjie,Ma Weiming,Nie Ziling.A proportional-resonant strategy for static medium frequency power supply[J]. Electronic Machines and Control,2012,16（10）：79-85（in Chinese）.

[2刘春喜,马伟明,孙驰.大功率400 Hz逆变电源数字控制设计[J].电工技术学报,2011,26（1）：100-107.

Liu Chunxi,Ma Weiming,Sun Chi,et al.Digital control design of high power 400Hz inverters[J].Transactions of China Electrotechnical Society,2011,26（1）：100-107（in Chinese）.

[3]Wheeler P W,Rodriguez J,Clare J C.Matrix converters：a technology review[J].IEEE Transactions on Industrial Electronics,2002,49（2）：276-288.

[4]Yamamoto E,Hara H,Uchino T,et al.Development of MCs and its applications in industry[J].IEEE Industrial Electronics Magazine,2011,5（1）：4-12.

[5]Zanchetta P,Wheeler P W,Clare J C,et al.Control design of a three-phase matrix converter based AC-AC mobile utility power supply[J].IEEE Transactions on Industrial Electronics,2008,55（1）：209-217.

[6]Arevalo S L,Zanchetta P,Wheeler P W,et al.Control and implementation of a matrix-converter-based AC ground power-supply unit for aircraft servicing[J].IEEE Transactions on Industrial Electronics,2010,57（6）：2076-2084.

[7]Mattavelli P,Marafao F P.Repetitive based control for selective harmonic compensation in active power filters[J]. IEEE Transactions on Industrial Electronics,2004,51（5）：1018-1024.

[8]Kouro S,Cortes P,Vargas R,et al.Model predictive control—A simple and powerful method to control power converters[J]. IEEE Transactions on Industrial Electronics,2009,56（6）：1826-1838.

[9]Cortes P,Ortiz G,Yuz J I,et al.Model predictive control of an inverter with output LC filter for UPS applications[J]. IEEE Transactions on Industrial Electronics,2009,56（6）：1875-1883.

[10]Rivera M,Rojas C,Rodriguez J,et al.Predictive current control with input filter resonance mitigation for a direct matrix converter[J].IEEE Transactions on Power Electronics,2011,26（10）：2794-2803.

[11]沈坤,章兢,王坚.一种多步预测的变流器有限控制集模型预测控制算法[J].中国电机工程学报,2012,32（33）：37-44.

Shen Kun,Zhang Jing,Wang Jian.A model predictive control scheme of multi-step prediction finite control set for converters[J].Proceedings of the CSEE,2012,32（33）：37-44（in Chinese）.

[12]Rodriguez J,Pontt J,Silva C,et al.Predictive control of three-phase inverter[J].Electronics Letters,2004,40（9）：561-562.