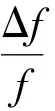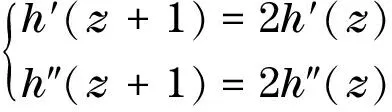涉及差分分担值的整函数唯一性
,
(上海理工大学 理学院,上海 200093)
1 问题的提出
本文中若不加其他说明,亚纯函数f(z)通常指在复平面亚纯,常数c∈泛指常数.采用文献[1-3]中Nevanlinna值分布理论中的记号及基本结论.
定义1λ(f),σ(f),σ2(f)分别表示f的零点收敛指数、级以及超级,对应表达式为
定义2设a(z)在上亚纯,若T(r,a)=o(T(r,f)),则称a(z)是f(z)的小函数.
定义3设f(z)亚纯,a为任一复数,若f(z)-a在上没有零点,则称a为f(z)的Picard例外值.
定义4若η为非零常数,定义差分和n阶差分算子
Δηf=f(z+η)-f(z)
定义5设f(z)与g(z)是区域D内的2个亚纯函数,a是一个复数.若f(z)-a与g(z)-a在D内有相同的零点,则称f与g在区域D内分担a,或称IM分担a.更进一步,若f(z)-a与g(z)-a在D内有相同的零点,并且所有的零点重级也相同,则称f与g在区域D内CM分担a.
1996年,Brücke[4]提出了著名的猜想.
猜想设f(z)为非常值整函数,超级有穷且不为正整数,若f(z)与f′(z)CM分担有限值a∈,则存在某常数c≠0,使得
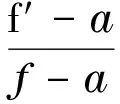
Brücke证明了a=0时的特殊情况[4],有穷级[5]以及超级小于1/2[6]的情况也已经被证明.2009年,Heittokangas等[7]研究了涉及差分算子的Brücke猜想,得到了定理1.
定理1设f(z)为级小于2的亚纯函数,c∈为非零常数.若f(z)与f(z+c)CM分担a∈与,则存在常数τ,使得
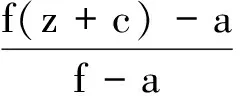
2015年,Shi等[8]将上述定理中的条件“分担常数a”推广为“分担小函数α(z)”,并考虑n阶差分情形,得到了定理2.
定理2设f(z)为级小于2的超越整函数,α(z)≠0为整函数,满足σ(α)<σ(f)和λ(f-α)<σ(f).若Δnf(z)-α(z)和f(z)-α(z)CM分担0,则α(z)为一个次数不超过n-1的多项式,f(z)具有如下的形式:
f(z)=α(z)+H(z)edz
式中:H(z)是一个多项式,满足cH(z)=-α(z);c,d是非零常数,满足ed=1.
随后Chen等[9]又将定理2中级小于2的条件放宽为有穷级,得到了定理3.

f(z)=a(z)+cec1z
式中,c,c1是非零常数.
最近,Liao等[10]又考虑了a(z)是Borel例外值小函数的情形,得到了定理4.
从而f(z)具有如下形式:
f(z)=a(z)+ceβz
式中,c,β是非零常数,满足
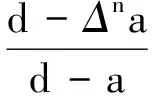
在此基础上,作者考虑将上述结论推广到超级小于1的超越整函数,得到了定理5.
定理5设f(z)是上的超越整函数,σ2(f)<1,且具有Picard例外周期小函数a(z).若f(z)与Δf(z)CM分担0,那么,f(z)=a(z)+setz,其中,s,t是非零常数.
2 引理证明
引理1[11]假设f1,f2,…,fn(n≥2)是亚纯函数,g1,g2,…,gn是满足下列条件的整函数:
b.gj-gk不是常数,1≤j c. 对于1≤j≤n,1≤h 则fj=0,j=1,2,…,n. 引理2[3]若f(z)是非常值的周期亚纯函数,则f(z)的级σ(f)与下级μ(f)都大于等于1. 引理3[3]若f(z)是上的亚纯函数,则f(z)和它的导函数有相同的级与下级. 引理4[3]若f(z)与g(z)是上的2个非常值的亚纯函数,级分别为σ(f),σ(g),则 σ(f·g)≤max{σ(f),σ(g)} (1) 现证明定理5. 证明由于a是f的Picard例外小函数,故f(z)=a(z)+eh(z),h(z)是整函数,σ(h(z))<1. 现分两种情况讨论. 情况1h(z)是超越整函数. eh(z+1)-eh(z)=aep(z)+eh(z)+p(z) (2) 现将排除3个相关的断言. 断言1σ(p(z))>σ(h(z)). 由式(2)可得 (eh(z+1)-eh(z))e0-(a+eh(z))ep(z)≡0 (3) 由断言1可得,σ(p(z))>σ(h(z+1)),于是 T(r,eh(z))=o(T(r,ep(z))) (4) 由引理1可得,f(z)≡0,与f(z)为超越整函数矛盾. 断言2σ(p(z))=σ(h(z)). 若h(z)=p(z)+c,则 eh(z+1)-p(z)-eh(z)-p(z)-a-eh(z)≡0 (5) 将中间两项合并,可得 eh(z+1)-p(z)-eh(z)=ec+a (6) 记ec+a=b.若b=0,有eh(z+1)-p(z)=eh(z),于是, h(z+1)-p(z)=h(z)+2kπi (7) 与h(z)=p(z)+c联立,可得 h(z+1)=2h(z)+2kπi-c 有 将两式相除,即得 于是,b≠0,又有h(z+1)-p(z)≠p(z)+h(z)+c.否则,类似式(7)得到矛盾.排除上述假设后,根据引理1即得矛盾. 再若h(z+1)-p(z)-h(z)≡c,则Δh(z)=p(z)+c,于是, eΔh(z)-p(z)-e-p(z)-ae-h(z)-1≡0 (8) 将第一项与最后一项合并为常数,同式(7)的证明方法,可以得到矛盾. 若上述情况未发生可直接由引理1得到矛盾. 断言3σ(p(z))<σ(h(z)). 则由式(2)可得 (9) 由引理1可以得到矛盾. 这时3个断言皆不成立,已经可以判定h(z)非超越整函数,情况1不成立. 情况2h(z)为多项式. 情况2的证明参见文献[12]. [1] CHEN C X.Complex differences and difference equations[M].Beijing:Science Press,2014. [2] LAINE I.Nevanlinna theory and complex differential equation[M].Berlin:Walter de Gruyter,1993. [3] YANG CC,YI H X.Uniqueness theory of meromorphic functions[M].Beijing:Science Press,2006. [4] BRÜCKE R.On entire functions which share one value CM with their first derivative[J].Results in Mathematics,1996,30(1/2):21-24. [5] GUNDERSEN GG,YANG L Z.Entire functions that share one value with one or two of their derivatives[J].Journal of Mathematical Analysis and Applications,1998,223(1):88-95. [6] CHEN Z X,SHON K H.On conjecture of R.Brück concerning the entire function sharing one value CM with its derivative[J].Taiwanese Journal of Mathematics,2004,8(2):235-244. [7] HEITTOKANGAS J,KORHONEN R,LAINE I,et al.Value sharing results for shifts of meromorphic functions,and sufficient conditions for periodicity[J].Journal of Mathematical Analysis and Applications,2009,355(1):352-363. [8] ZHANG J,KANG H Y,LIAO L W.Entire functions sharing a small entire function with their difference operators[J].Bulletin of the Iranian Mathematical Society,2015,41(5):1121-1129. [9] CHEN C X,CHEN Z X.Entire functions and their higher order differences[J].Taiwanese Journal of Mathematics,2014,18(3):711-729. [10] LIAO L W,ZHANG J.Shared values and Borel exceptional values for high order difference operators[J].Bulletin of the Korean Mathematical Society,2016,53(1):49-60. [11] HALBURD R,KORHONEN R,TOHGE K.Holomorphic curves with shift-invariant hyperplane preimages[J].Transactions of the American Mathematical Society,2014,366(8):4267-4298. [12] SHI X J,LIAO L W,ZHANG J.On a polynomailpsuch thatp(Δnf) andp(f) sharing a small function[J].Houston Journal of Mathmatics,2017,43(2):345-361.3 定理5证明