电网谐波电压对同步调相机转子损耗的影响

许国瑞，李金香，吴国栋，孙玉田，康锦萍



电网谐波电压对同步调相机转子损耗的影响

许国瑞1，李金香2，吴国栋1，孙玉田2，康锦萍1

（1. 华北电力大学电气与电子工程学院，北京 102206；2. 水力发电设备国家重点实验室(哈尔滨大电机研究所)，哈尔滨 150040）

高压直流输电系统单极大地回线运行会使得附近变压器产生直流偏磁现象，增加变压器副边电压的谐波含量。当变压器与为换流站提供无功支撑的同步调相机连接时，谐波电压会影响同步调相机的转子损耗。本文针对不同谐波电压下，同步调相机转子损耗的变化展开研究。采用时步有限元法计算了同步调相机空载、进相以及迟相运行条件下，谐波电压对转子铁心和槽楔损耗的影响，对比分析了转子各部分损耗大小随电压谐波次数的变化规律。研究结果为同步调相机的安全可靠运行提供了理论基础。

同步调相机；转子损耗；谐波电压；直流偏磁

0前言

在直流系统动态调整过程中，直流本身并不能够提供动态无功。随着远距离直流输电的规模化建设，无功储备和电压支撑不足的问题突出，电压稳定问题严重。针对高压直流输电系统要求，大规模有功输送必须在换流站提供大量无功功率作为支撑，而同步调相机具有调节能力受系统影响小，高/低压穿越能力强，动态维持电压能力强等优点[1]。其既可以为系统提供短路容量，具有良好的无功出力，又可提高整个系统的稳定性[2-4]，因此将同步调相机安装于直流输电系统的送端和受端，可为换流站提供无功补偿，同时可以提高输电系统的稳定性。当直流输电系统以单极大地回线方式运行时，会在数千公里范围内的大地上产生一个直流电位分布，位于上述区域内的电力变压器，其直流接地电极的漏电流会通过变压器星型连接绕组的接地中性点进入到交流电力系统，继而产生直流偏磁现象[5-6]。直流偏磁电流会使变压器铁心中的磁场发生偏置，造成铁心的半波过饱和[7]。这种现象将对电力变压器电磁特性、损耗、噪声及谐波含量造成较大的影响[8]。文献[9]指出直流偏磁会导致变压器的副边电压中产生大量的谐波分量；文献[10]介绍采用监测网络系统监测磁暴引起的变压器直流偏磁现象，得出直流电流最大为83A，最大谐波电压占基波4%。文献[11]报道了2004年5月贵广I回工程单极大地回线运行时，测量到春城变电站主变压器中性点的直流电流为34.5A，噪声93.9dB，谐波电压总畸变率2.1%。

在高压直流输电的换流站，同步调相机作为无功补偿设备通过变压器为系统提供无功支持。当变压器的二次侧与同步调相机连接时，这些谐波电压会在同步调相机的定子绕组中产生相应的谐波电流。由于同步调相机机端星接且通过高阻接地，因此3的倍数次谐波电压（3次、6次、9次等）产生的谐波电流不会流入同步调相机；而其它阶次的谐波电压所产生的谐波电流均会在气隙中产生相对于转子运动的气隙磁动势。正序电流在气隙当中产生与各次谐波相同频率向前旋转的磁场，负序电流在气隙当中产生以谐波频率相对于转子旋转方向向后旋转的磁场，这些磁场在转子铁心和槽楔中均感应电流及相应的谐波损耗。因此研究不同谐波电压对产生损耗的大小的影响对于同步调相机的安全稳定运行具有重要意义。

为了研究不同谐波电压对同步调相机转子损耗的影响，本文建立了用于分析谐波电压对同步调相机转子损耗影响的场-路耦合时步有限元模型。通过计算同步调相机空载、进相以及迟相运行条件下，机端电压不同谐波分量对转子铁心和槽楔损耗的影响，对比分析了转子各部分损耗大小随电压谐波次数的变化规律。研究结果为同步调相机的安全稳定运行提供理论基础。

1 同步调相机场-路耦合时步有限元模型

1.1 时步有限元模型

采用二维有限元来描述同步调相机，假设定转子各绕组端部漏抗为恒值，不计铁心磁滞效应，由麦克斯韦方程组可得同步调相机场路耦合方程[12]：

式(1)中，是磁势向量，是刚度矩阵，C，C分别是定子电流和励磁电流的关联矩阵，D，D是转子槽楔和铁心涡流的关联矩阵，U是发电机的端电压，s，f分别是定子电流和励磁电流。l=[A,B,C]，s=[A,B,C]，s=diag[s,s,s]，s=diag[s,s,s]，s和s分别为定子绕组的电阻和端部漏电感。

同步调相机转子损耗主要包括转子铁心和转子槽楔两部分结构中产生的损耗。同步调相机的转子导电槽楔通过端部的梳齿环或护环共同构成发电机的阻尼回路。阻尼回路模型如图1所示，通过对阻尼回路列写方程计算转子槽楔中的损耗。

图1 阻尼回路模型

图1中di、di分别为阻尼端环的电阻与漏电感，bi为阻尼导条电流，di为回路电流，di为导条两端电压。阻尼导条直线部分各点电流密度d1i表示为：

根据图1，或得各支路电流方程与回路电压方程：

结合式(2)与(3)，经有限元离散可得阻尼回路方程：

式中，d=[d1…di…dk]T，d=[d1…di…dk]T，d=diag[2d1,…,2dk]，d=diag[2d1,…,2dk]，d=diag[2d1,…,2dk]，d1=diag[σS/ef,…,σS/ef]，d2=－dΔe/3，Id，Ud转换矩阵。

结合式(1)和(4)，可得到计及转子槽楔构成阻尼回路的同步调相机场-路耦合时步有限元模型：

式(5)中发电机机端电压U既包含基波电压也包含不同次数的谐波电压，可表示为：

式中，U、U、U为同步调相机机端电压中的基波和谐波分量。

1.2 转子损耗计算

同步调相机转子槽楔和转子铁心中所感应电流的大小取决于切割磁场以及材料磁导率的大小，图2中转子槽楔和铁心当中所感应的涡流密度的大小可以表示为：

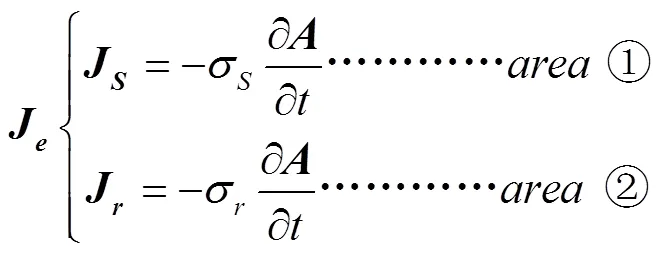
式中，σ和σ分别是定子槽楔和转子铁心的磁导率。

由于同步调相机的转子铁心为实心钢结构，因此主要考虑铁心中的涡流损耗，忽略铁心中的磁滞损耗。转子铁心中感应电流的机理与槽楔中相同，因此计算转子铁心损耗的方法与计算转子槽楔损耗的方法相同。转子槽楔和铁心中的这些涡流损耗可以通过如下所示的有限元计算方法计算[13]：

式中，PSW为转子槽楔损耗；PIC为转子铁心损耗；Ss_e为转子槽楔的截面积；Sr_e为转子铁心的截面积；Jr_e为转子槽楔的涡流密度；T为周期。

1.3 转子损耗机理分析

当同步调相机所连接的电网电压按正弦规律变化时，由励磁电流产生的基波磁场和谐波磁场相对于转子静止，不会在转子绕组中感应涡流并产生损耗。定子三相基波电流产生的磁场中包括基波磁场以及6±1次的谐波磁场。基波磁场的转速相对于转子的转速为零，其不在转子中产生损耗；而谐波磁场相对于转子的转速不为零，它们会切割转子绕组并产生涡流损耗。例如，由定子基波电流产生的5次谐波磁势的极对数和速度分别为基波磁势的5倍和1/5，且转速为反向旋转，因此该谐波磁势在转子绕组中感应电流的频率是基波的6倍；由定子基波电流产生的7次谐波磁势的极对数和速度分别为基波磁势的7倍和1/7，且转速为正向旋转，因此该谐波磁场在转子绕组中感应电流的频率是基波的6倍。

当同步调相机所连接的电网电压包含谐波分量时，这些谐波电压对应的谐波电流所产生的磁场不同于基波电流产生的磁场，谐波电压对应转子涡流的频率见表1。该表列出了2~7次谐波电压对应的转子涡流频率，根据表中的规律可以继续分析更高次的谐波电压对应的转子涡流频率，但由于谐波电压次数越高，其幅值越小，通常高次谐波电压对应的转子涡流可以忽略。由于同步调相机三相通常采用星型接线，且中性点不直接接地，而3的倍数次谐波电压的相位均相同，因此其不会在定子绕组中产生相应的电流和磁场，也就不会在转子中感应涡流。2次和4次谐波电压均在转子中感应3倍频的涡流；5次和7次谐波电压均在转子中感应6倍频的涡流。

表1 谐波电压对应转子涡流的频率

2 不同谐波电压对同步调相机转子损耗的影响

为了研究不同谐波电压对转子槽楔损耗和铁心损耗的影响，将机端电压源设为理想电压源及分别含3%的各次谐波分量的电压源，依次计算同步调相机在空载运行、迟相运行以及进相运行时的转子损耗，对各情况下转子槽楔和铁心损耗进行对比和分析。

2.1 同步调相机空载运行时的转子损耗对比

当同步调相机空载运行时，计算了同步调相机机端电压为理想电压源以及分别含2~7次谐波分量电压源时的转子槽楔损耗和铁心损耗。对比分析了不同谐波电压对转子损耗的影响，一个工频周期内转子槽楔损耗曲线如图3(a)所示，铁心损耗如图3(b)所示。同时，对比了一个工频周期内转子槽楔及铁心中的平均损耗，结果见表2，表中P和P分别表示一个工频周期内的转子平均槽楔损耗和铁心损耗。

通过对图3及表2的结果进行对比，可以得出：

（1）机端电压中含3的倍数次谐波分量时同步调相机转子槽楔损耗和铁心损耗均与理想电压源时相同，即机端电压中3的倍数次谐波分量不会在转子中产生损耗。

（2）机端电压中含除3的倍数次以外谐波分量时，同步调相机转子槽楔损耗与铁心损耗明显增大，含2次谐波电压时转子损耗最大；转子铁心中的损耗远大于槽楔中的损耗，含2次谐波电压时转子铁心损耗是槽楔损耗的7倍。

表2 空载运行时同步调相机转子平均槽楔损耗与铁心损耗

2.2 同步调相机迟相运行时的转子损耗对比

当同步调相机迟相运行时，计算了机端电压为理想电压源和含2~7次谐波分量电压源时的转子槽楔损耗和铁心损耗，此时同步调相机向电网发出274MVar无功功率。对比分析了不同电压源对转子损耗的影响，转子槽楔损耗曲线如图4(a)所示，铁心损耗如图4(b)所示；一个工频周期内转子槽楔及铁心中的平均损耗见表3。表中，ξ为含谐波分量电压源时同步调相机的槽楔损耗相对于理想电压源时槽楔损耗的倍数，ξ为含谐波分量电压源时同步调相机的铁心损耗相对于理想电压源时铁心损耗的倍数。

表3 迟相运行时同步调相机转子平均槽楔损耗与铁心损耗

通过对图4及表3计算结果对比分析，可以得出：

（1）在不同机端电压下，转子槽楔损耗均小于铁心损耗；机端电压中含2次谐波分量时，转子铁心损耗约为槽楔损耗的6倍；随着谐波次数的增加，两者差距逐渐缩小，含7次谐波分量时转子铁心损耗为槽楔损耗的4.75倍；当机端电压为理想电压源时，转子铁心损耗约为转子槽楔损耗的4.5倍。

（2）机端电压中含除3的倍数次以外的谐波分量时，随着电压谐波次数的增加，转子槽楔损耗和铁心损耗均逐渐下降。机端电压中含2次谐波分量时，转子槽楔和铁心损耗分别为理想电压源情况下损耗的3倍和4倍。

2.3 同步调相机进相运行时的转子损耗对比

当同步调相机进相运行时，计算了同步调相机机端电压为理想电压源以及分别含2~7次谐波分量电压源时的转子槽楔损耗和铁心损耗，此时同步调相机从电网吸收144MVar无功功率。对比分析了不同电压源对转子损耗的影响，转子槽楔损耗曲线如图5(a)所示，铁心损耗如图5(b)所示；一个工频周期内转子槽楔及铁心中的平均损耗见表4。

表4 进相运行时转子平均槽楔损耗与铁心损耗

根据以上结果可以得出如下结论：

（1）同步调相机进相运行时，转子铁心和槽楔中的损耗相对于迟相运行时减小，但大于空载运行下铁心和槽楔损耗。机端电压为理想电压源时，转子槽楔和铁心中的损耗分别是迟相运行时的29.76%和29.67%。

（2）机端电压中含除3的倍数次以外的谐波分量时，随着电压谐波次数的增加，转子槽楔和铁心当中的损耗逐渐减小。机端电压中含有2次谐波分量时，转子铁心和槽楔损耗最大，分别约为理想电压源下的8.56倍和12.35倍。

3 结论

通过对比分析不同谐波电压对同步调相机转子损耗的影响，得出如下结论：

（1）由于机端电压中3的倍数次谐波分量不会在定子绕组中产生相应的谐波电流，因而在转子中产生的损耗为零，此时同步调相机转子槽楔损耗和铁心损耗均与理想电压源时相同。

（2）不论机端电压是否含有谐波分量，转子槽楔中的损耗均小于转子铁心中的损耗。机端电压中含有2次谐波分量时，转子槽楔和铁心损耗最大；除3的倍数次谐波外，随着谐波电压次数的增加，转子槽楔损耗和铁心损耗均逐渐减小。

（3）同步调相机进相运行时的转子损耗明显小于迟相运行时的转子损耗。机端电压为理想电压源时，同步调相机在进相运行下的转子槽楔损耗和铁心损耗分别为迟相运行时的29.76%和29.67%。

[1] 张文亮, 于永清, 李光范, 范建斌, 宿志一, 陆家榆, 李博. 特高压直流技术研究[J]. 中国电机工程学报, 2007, 27(22):1-7.

[2] Sercan Teleke, Tarik Abdulahovic, Torbjörn Thiringer, et al. Performance comparison of synchronous condenser and SVC [J]. IEEE Transactions on Power Delivery, 2008, 23(3):1606-1612.

[3] 刘振亚, 张启平, 王雅婷, 董存, 周勤勇. 提高西北新甘青750kV送端电网安全稳定水平的无功补偿措施研究[J]. 中国电机工程学报, 2015, 35(5):1015-1022.

[4] Katsuya Y, Mitani Y, Tsuji K. Power system stabilization by synchronous condenser with fast excitation control[C]// International Conference on Power System Technology, 2000. Proceedings. Powercon. IEEE, 2000:1563-1568 vol.3.

[5] 罗建武, 罗文杰. 偏磁的起因和消除方法[J]. 电工技术学报, 1999, 14(6):73-77.

[6] 何俊佳, 叶会生, 林福昌,等. 土壤结构对流入变压器中性点直流电流的影响[J]. 中国电机工程学报, 2007, 27(36):14-18.

[7] E. Bernabeu. Single-phase transformer harmonics produced during geomagnetic disturbances: theory, modeling, and monitoring [J]. IEEE Trans. Power Del., 2015, 30(3):1323-1330.

[8] Zhang B, Zhao J, Zeng R, et al. Numerical Analysis of DC Current Distribution in AC Power System Near HVDC System[J]. IEEE Transactions on Power Delivery, 2008, 23(2):960-965.

[9] Pan Z, Wang X, Mei G, et al. A transformer neutral current balancing device to restrain half-cycle saturation induced by HVDC monopolar operations[J]. Electric Power Systems Research, 2016, 132:104-114.

[10] Lesher R L, Porter J W, Byerly R T. SUNBURST-a network of GIC monitoring systems[J]. Power Delivery IEEE Transactions on, 1994, 9(1):128-137.

[11] 尚春. HVDC地中电流对交流变压器影响的抑制措施[J]. 高电压技术, 2004, 30(11):52-54.

[12] Xu Guorui, Liu Xiaofang, Luo Yingli, Zhao Haisen. Influence of Different Practical Models on the First Swing Stability of Turbine Generators[J]. Electric Power Components and Systems, 2015, 43(2):212-223.

[13] Likun Wang, Weili Li, Feiyang Huo, Shukuan Zhang, and Chunwei Guan. Influence of Under excitation Operation on Electromagnetic Loss in the End Metal Parts and Stator Step Packets of a Turbo-generator[J]. IEEE Trans. on Energy Conv., 2014, 29(3):748-757.

The Influence of Harmonic Voltages on Rotor Loss of Synchronous Compensator

XU Guorui1, LI Jinxiang2, WU Guodong1, SUN Yutian2, KANG Jinping1

(1. School of Electrical and Electronic Engineering, North China Electric Power University, Beijing 102206, China; 2. State Key Laboratory of Hydropower Equipment (Harbin Institute of Large Electrical Machinery), Harbin 150040, China)

When the HVDC system operates in a mono-polar earth return line, the nearby electrical transformers are affected by DC bias phenomenon which will generate harmonic components in the secondary voltage of the transformer. The synchronous compensator which provides the reactive power for the converter station is connected to the electrical transformers, the harmonic voltage will affect the rotor loss of the synchronous compensator. In this paper, the effects of different harmonic voltages on the rotor losses of synchronous compensator are studied. The influence of different harmonic voltages on the loss of rotor core and slot wedge under no-load, leading phase and lagging power factor operation are calculated based on time-stepping finite element method. The results provide a theoretical basis for the safe and stable operation of the synchronous compensator.

synchronous compensator; rotor loss; harmonic voltage; DC bias

TM342

A

1000-3983(2018)01-0028-06

2017-06-10

许国瑞（1986-），毕业于华北电力大学电机与电器专业，研究方向为同步发电机模型及参数，博士研究生。

国家自然科学基金资助项目（51507059）；中央高校基本科研业务费专项资金资助（2018MS10）