终是关联关不住，贤纲秋水做文章

刘俊明

我以为，物理学中最难的领域是凝聚态物理。基本粒子物理、核物理和高能物理，也许在学术上很难，但她们距离口味不同的百姓相当远，还能够“唯心主义”地发挥猜想的空间较大，受外部非科学的压力较小。凝聚态物理因为几个特征，一直以来“满是光芒尽是伤”：(1)体系对象广泛，学者们素有喜新厌旧、见异思迁的秉性，所以凝聚态的新东西多、新故事好。(2)研究工具是文明富裕的单调增函数，过去几十年，很多研究机构装备齐全先进，所以凝聚态物理追逐的气氛很浓。(3)下盘很扎实、范式也相对固定，继续长高变得相对困难。(4)接地气，在街头跟百姓秀凝聚态的功用并不费力，但也常常因为我们口才不佳或心高气傲而常受地气熏冲，受夹板气的风景也不少。(5)在凝聚态中讨生活的人多，有统计数据表明物理学家有70%在凝聚态领域吃草产奶。也因为如此，凝聚态物理牛人辈出，上顶着物理学若干基本问题的天，下接着百姓平民生活一丁一卯的地，经常是望风得雨、洗尽铅华又一春的节奏。

这是一段发生在2011年的历史小故事，是凝聚态物理之沧海一粟。

量子凝聚态物理关注电子电荷、自旋和轨道自由度，更关注这些自由度因对称破缺导致的新物态和新效应，分支繁杂、领域深邃、纵横交错，其中一个分支是关联量子物理。因为引入关联（哈伯德U），这些自由度相互竞争调控，蕴含难以测度的新物理与新现象，也因此得宠至今。关联量子凝聚态物理的出发点如图1所示，其中左图是量子凝聚态物理的主要领域，右图显示关联在其中的重要作用！只是，这两个圈中任何一个名词都令人眩晕，当这么多“物理”搅合在一起时，“直教人生死相许”就变成一种日常生活。

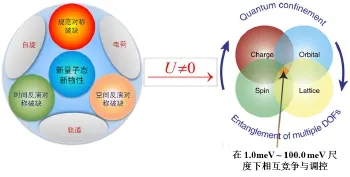
FIG.1量子凝聚态物理中关联（哈伯德U）的沙砾：一沙一世界、一圆万重天。

量子凝聚态的另外一个分支自然是量子拓扑物理了。这一领域过去几年喧嚣尘上，看君听得看得太多，自有疲劳之感。因此，看君可略去以下三万字不读。我只说其中与自旋–轨道耦合(SOC)相关的拓扑量子态。从一般Mott绝缘体到量子Hall效应、再到量子自旋Hall效应，引入SOC使得固体电子系统中拓扑量子相开始浮现出来，最近几年诞生了一系列重要结果，而且成果产出目前尚未到达饱和，如图2所示。2011年之前，拓扑量子态最重要的角色是拓扑绝缘体 (TI)，而拓扑超导体则是展现拓扑绝缘体更加令人神往的分支，赚足了眼球，直至今日依然没有定论。拓扑绝缘体源于SOC较强的Mott绝缘体，在体系表面处因为毗邻真空（空间对称性破缺）而在带隙中形成两条与自旋相关的能带，如图2右边所示。如果在动量空间求积此能带，结果是一个拓扑数（如拓扑陈数），是为拓扑态。这里，吸引我等百姓眼球的无非两点：(1)两条能带在带隙中交叉（红线和蓝线），形成一个狄拉克交叉点 (Dirac point)，因为此点附近的能带色散关系接近是线性的，体系表面处载流子迁移率会很高。这个很有用if any。(2)这一拓扑态满足时间反演对称性，因此对磁性不敏感，或者说对磁杂质等很 robust。这个也很有用if any。这两个特性赋予了拓扑绝缘体明确的应用优势，非常好地体现了凝聚态物理的特点：很学术（阳春白雪），又很有潜在应用（下里巴人）！

不过，做材料的人知道，如果这个表面态必须是几何学上的二维表面，应用起来未必容易，因为实际材料表面要处理到什么程度才算是二维表面态？这大概是目前利用TI表面态的器件还待字闺中的主要原因吧？

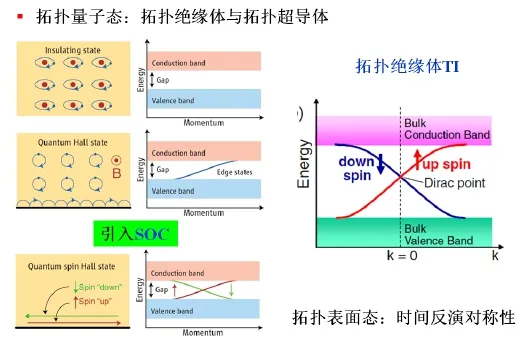
FIG.2自旋–轨道耦合SOC触发的几种量子物态：从Mott绝缘体到量子Hall态，又到量子自旋Hall态，再到拓扑绝缘体TI态。

FIG.3 2011年前后拓扑量子态的框架。具有拓扑绝缘体态的体系具有(1)强SOC，(2)满足时间反演对称（也就是非磁性），(3)体态是绝缘体。那时候的物理坐标就是图中的纵轴，即SOC的大小。物理学家都是人精，一旦确立这些观点，接下来对拓扑绝缘体是要杀要剐，一目了然。科学问题是：(1)如果引入哈伯德关联U会怎么样？(2)如果引入磁性破坏时间反演对称会怎么样？(3)体态能不能无能隙？即体态必须得是绝缘体吗？

FIG.4 2011年，向拓扑量子态中加入量子关联 U的尝试(Yu S L.et al,Phy.Rev.Lett.,107,11:010401)。上部显示了(SOC,U)空间的理架构和所研究的模型哈密顿。下部所示为SOC强度与U所在空间中的一系列量子态：SM-semi-metal,SL-spin liquid,TBI-topological band insulator,AF-antiferromagnetic。

我们回顾总结2011年前后对拓扑量子态的认识，大约就是图3所示的样子。现状和关键科学问题今天看来一目了然，但当时未必是“竹外桃花三两枝，春江水暖鸭先知”的，只是，自从世上有了精明过人的物理学家，“萎蒿满地芦芽短，正是河豚欲上时”就是必然。2011年南京大学的李建新课题组（于顺利）和北京大学谢心澄老师合作，首先在一个基于单电子作用、可描述拓扑绝缘体态的Kanee-Mele模型中引入量子关联U，思路和模型哈密顿显示于图4上部。李建新他们解析这一新的哈密顿，获得一系列准粒子激发谱，展示了SOC强度和关联强度U所在空间的量子相图，如图4下部。显而易见，U的加入促使拓扑绝缘体态向关联量子态的转变，预示出U对拓扑量子态可能不是一个好的物理。当然，如图绿色箭头所示，从U=0走向紫色的关联量子区域，中间也经历了一些好的物理态，如TBI态、自旋液体态。这些中间态的存在提示U未必就一定是拓扑态的死敌，为随后万贤纲粉墨登场埋下伏笔。

有了李建新谢心澄他们的第一步，再加上破坏时间反演对称的磁性，就成为物理上的必然，如图5左边所示。由于拓扑绝缘体的工作，我们早前已经可以构建图5右边的相图。不过，看君别像我这般不知天高地厚、得意乐观，这里的困难是难以衡量的。比如，要构建一个含有SOC、U和M的哈密顿模型并能够解析，本身就是一个很可能无解的课题，也许难住了诸如谢心澄这样的凝聚态理论高手。凝聚态物理在这个时候会很怀念量子理论和统计物理勃发时代的大师们，他们那时恣意妄为、不拘一格，将凝聚态的下盘夯实到位，留给现在高手们的都是一些拓扑态缺陷，已经难以撼动了。

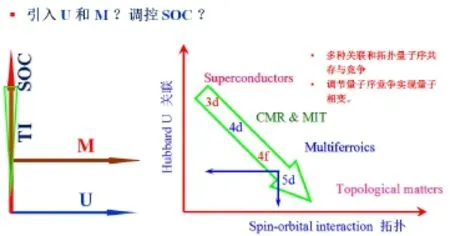
FIG.5三个物理元素SOC、U和磁性M共存的体系蕴含新的物理效应。右边是SOC和U空间的拓扑量子相图：CMR-庞磁电阻,Multiferroics-多铁材料,topological matters-拓扑态。

接下来，花开两朵、各表一枝。

第一支是万贤纲。他学地质出身，研究生阶段转行学理论凝聚态物理。这种现象在南京大学是热力学自发过程。我知道的还有朱诗亮、高兴森等物理人，也是学地质出身。他们有那种踏实用功的品质，厚积而薄发，十年八年之后其理论功底反而比很多物理科班们更胜一筹。万贤纲外形魁伟，但不修边幅，是个地质汉子的模样，但内心其实书生气浓厚、性格耿直。这种性格大概很适合做理论。我认为万贤纲与其合作者一直在做的就两件事：(1)发展第一性原理计算方法学，包括DMFT这种很难“顾名思义”的方法；(2)复杂关联体系的磁有序。这是两项非常重要、又损己利人的课题，但也为贤纲打下雄厚的理论基础和培养出敏锐的物理感觉。这个过程持续了很长时间，万贤纲在慢慢走向45岁这个中国年轻优秀学者都很恐惧的年龄，期间他的几项工作虽然瞧不上PRL，但也没有达成一展抱负的心愿。我用过去一首旧作来描绘贤纲的心境也许还算合适（图6：苏幕遮@晚秋）：

FIG.6苏幕遮@晚秋：短秋疏，长静夜。独寐书斋，独对窗前月。暮色寒天惊落叶，不似飞花，更似花枯谢。砚闲愁，思冷阕。十载唐楼，且任余晖曳。今日夕阳吾可舍？纸墨人生，一笔狂风写！

第二支是图5这个框架。贤纲一直对复杂过渡金属化合物的磁有序很感兴趣，并的确颇有收获。这个课题好像一直是他的保留曲目。2010年前后，他游荡到5d氧化物体系，开始计算Y2Ir2O7这类强失措体系的磁基态。我们知道，这种烧绿石四面体堆砌体系的磁结构非常复杂。他花了很长时间确定这个体系的基态是5d自旋指向全进或全出(all in/all out)。万贤纲随后经过细致深入的计算，得到了诸如图7这样的能带结构，并清晰地意识到了其中的反常，如图题所述。这样的结构还不止一处，在三维动量空间中零零落落有一些。值得注意的是，这里是体态、不是拓扑绝缘体那种表面态。体态的导带–价带发生了物理学上的kiss，即形成了狄拉克点(Dirac point)。

这类狄拉克点与诸如石墨烯等狄拉克半金属不同，令人极度疑惑不解。这种时候，一个学者的物理感觉就起到了关键作用。我的马后炮分析当然显得得心应手，问题是疑惑有了，答案还会远么！

疑惑在于：(1)这是一个体态Dirac点，因此是半金属无疑。但kiss不发生在高轴也不发生在常见的主轴上，令人不解。(2)这是一个Dirac半金属？这个体系是有磁性的，也就是说时间反演对称性是破坏了的，怎么可能满足时间反演对称的四分量Dirac方程？(3)布里渊空间中这种体态有很多个，对本体系而言有24个之多，这是什么？

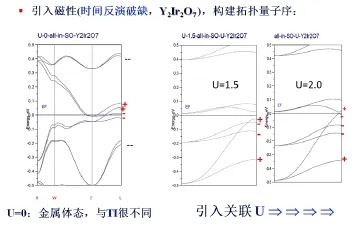
FIG.7烧绿石四面体堆砌结构Y2Ir2O7化合物的电子结构：左边是U=0的电子结构，它是一个金属态。因为这是一个关联系统，加U是必然的。万贤纲加U后的电子结构显示于右边。这个结果令人费解之处有二：(1)加U后电子结构并没有如常态物理那般打开能隙，这非常异常；(2)从能带的对称性来看，加U不但没有打开能隙，反而使得能带的宇称(parity)出现了反转。这是又一个反常的结果，意味着反常量子态的存在。

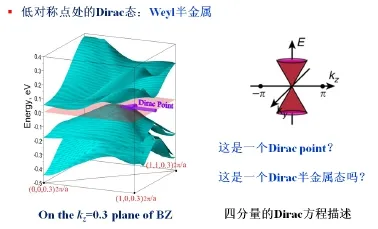
FIG.8烧绿石四面体堆砌体系Y2Ir2O7化合物电子结构的三维细节。

FIG.9威尔半金属(Weyl semimetal)拓扑体态的物理根源：（（上部）对于一个 1/2-spinor，在时间反演和空间（宇称）反转对称性保持的前提下，半金属态用四分量狄拉克方程描述。如果存在时间反演破缺或者宇称破缺，狄拉克方程可以简化，体系会蜕变为所谓的威尔(Weyl)方程描述的一对半金属态。这一对威尔态具有相反的手性，一个是左手性时另一个一定是右手性。（下部） 对应地，一个狄拉克点就蜕化为布里渊空间中的一对威尔点。如果这一体系在布里渊空间存在有限边界，则这一对威尔点一定会通过所谓的表面费米弧(Fermi Arc)联系起来。这些特征首次定义出一个新的量子拓扑态—威尔半金属(Weyl Semimetal)体态，并具有有限的费米弧特征。事实上，在整个布里渊空间寻找，Y2Ir2O7中存在12对一共24个威尔点。

万贤纲及其合作者带着这些疑问，给出了如图9所示的精彩答案(Wan X G,et al.Phy.Rev.B,2011,83:205101)。比较物理的阐述语言是：Weyl Semimetal的相关效应应该还在研究，它中间有gapless的拓扑保护体态。一个时间T和宇称P都不破缺的体系，只能存在Dirac形式的gapless态，它有四个自由度。而当T、P同时破缺的时候，就会分裂成两个 Weyl费米子。这时体态就成为Weyl半金属。一个Dirac费米子有四个自由度，在特定的表象下分解成各为两个自由度的正能/负能或者正手性/负手性。Weyl费米子就是在手性表象下的Dirac费米子的正/负手性的部分，仅含有两个自由度。一个Dirac point可以看做两个手性相反的Weyl费米子，Weyl Semimetal的拓扑保护性之来源于破坏T或者P的对称性，使Weyl费米子在k空间分开，成为独立的Weyl费米子。

看君都知道，Weyl方程是德国知名数学物理学家Weyl从Dirac方程推演出来的，用于描述中微子。后来通过中微子振荡实验发现中微子有质量，Weyl的预言未曾上阵就刀枪入库马放南山。Weyl半金属是凝聚态物理借鉴高能和粒子物理的又一个事例，从此成为拓扑量子凝聚态的一个新分支，至今依然如火如荼。不过，要验证贤纲预言的Y2Ir2O7这个体系是否存在Weyl半金属态，实验上首先要获取磁基态的样品，这绝非易事。杨振宁先生声言狄拉克的文章属“秋水文章不染尘”一类。万贤纲的Weyl半金属态源于狄拉克，算是仰望狄拉克之芸芸晚辈，他的这一工作也有点“秋水文章”的味道，只是目前还真是“不染尘”的状态，直到现在也未预言成真，虽然据说最近也有点苗头。当然，这里的“不染尘”并非邓石如自题联的那般“不染尘”。不久，中科院物理所几位顶尖高手预言了空间反演对称破缺体系也能够实现Weyl半金属态，并很快找到TaAs这样的精妙体系，最终发现Weyl半金属存在于凝聚态之中。与此同时，美国一批名家学者也独立报道了类似发现。看君一定看过很多有关这一巨大进展的科普文章，我在此就不再班门弄斧或王婆卖瓜了。

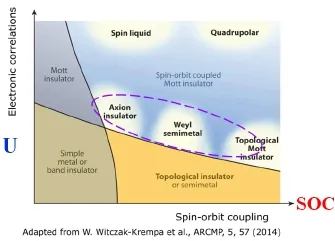
FIG.10 2014年拓扑量子凝聚态的图景。

FIG.11 CaTe化合物中拓扑 node-line半金属态的能带结构，其中能带闭合 loop和 M 点出的平坦 (flat)形态一目了然(来自万贤纲课题组论文)。

到目前为止，除去物理上的意义，Weyl半金属如何接地气好像还是一个问题，也许在量子计算和新型信息表达方面有所期待。但无论如何，继拓扑绝缘体之后，Weyl半金属拓扑量子态的出现倒是给拓扑量子物理坐实了凝聚态物理排头兵的岗位。2014年有人总结了拓扑量子态的新世界，如图10所示，这里的右侧和上部没有边界，显示了开放的图景，阐释了“拓扑如此多娇，引无数贤纲竞折腰”的模样。过去几年，国内外拓扑人辗转踌躇、夜不能寐，在寻找各种可能突破的途径。

万贤纲作为其中一员，也在左冲右突。最近，他和合作者开始关注新的拓扑态。2012年前后，加州大学圣巴巴拉的Leon Balents等人曾经提出过topological node-line semimetal量子态的理论方案，其中某个高对称点处的能带形成闭合的loop和平坦(flat)的形态，应该是实现拓扑超导一个有吸引力的方案。但Balents等人可能是因为太牛而不屑于接地气，对具体哪些体系能够实现这一node-line semimetal拓扑态漠不关心，亦或是真的去找也很困难。现在国内外已经预言了一些材料具有这一特征。贤纲及其合作者找到了一个更为简洁的体系 CaTe，成分和结构简单、制备合成也应该不难，应该能够引起实验者关注，其能带结构如图11所示。去年，万贤纲课题组以“CaTe:a new topological node-line and Dirac semimetal”为题在《npj Quantum Materials》撰文，阐述 了他们如何通过计算来确认 CaTe就是 node-line semimetal(http://www.nature.com/articles/s41535-016-0005-4)。看君如果愿意，可移步Du Yong-Ping（杜永平）等人2017年1月23日发表在《npj Quantum Materials》上的论文(http://www.nature.com/articles/s41535-016-0005-4)（阅读下载都是免费的）。