差分卫星导航系统定位精度飞行测试方法

，，,

(中国飞行试验研究院，西安 710089)

0 引言

当前我国机载差分卫星导航系统由差分GPS和差分BDS组成，且卫星导航定位方式也由过去的单点定位到伪距差分定位，再到目前定位精度更高的载波相位差分，定位精度也由10m级到米级再到厘米级[1-2]。目前国内差分卫星导航设备大多用于地理信息测绘、高精度导航定位用途。民航飞机和无人机逐步开始应用差分卫星导航系统，并且形成了以差分卫星导航设备为依托的地基增强系统(Ground Based Augmentation System, GBAS)，世界上已有多个国家在进行基于GPS的GBAS研究，我国也开始了基于BDS的GBAS研究[3]。

机载差分卫星导航系统最重要的指标就是定位精度。针对如何对机载高精度差分卫星导航系统定位精度考核的问题，本文提出了一种飞行测试验证方法。在精度计算过程中，由于两部差分卫星导航设备卫星天线在空间中并不是重合的，因此采用基于消除杆臂效应的数据处理方法对精度的测试是不可或缺的，可以消除测试过程中引入的较大计算误差项。

1 差分卫星导航系统组成

差分卫星导航系统由机载终端和地面差分站组成，均由数传电台和卫星导航接收机及对应天线组成，如图1所示。伪距差分是应用成熟度最高的差分定位技术之一，差分站上的卫星接收机测得与所有可视卫星的测量距离，并将自身真实坐标与各卫星的距离进行比较，求出测量距离和真实距离之间的偏差(即差分修正量)，通过数传电台将修正量发送给机载差分终端，经机载终端处理从而达到提高定位精度的目的。

图1 差分卫星导航系统组成框图Fig.1 The composition diagram of differentialsatellite navigation system

载波相位差分技术又称为RTK技术，差分站的卫星接收机连续观测卫星并将自身坐标信息通过数传电台发送给机载卫星终端。机载卫星接收机接收卫星载波的同时，又接收来自差分站的载波观测量和坐标值，经实时数据处理解算自身的坐标结果，提高定位精度。

机载差分卫星导航系统的飞行试验主要考核了包括定位精度、完好性、覆盖范围、信号质量等指标[4]，本文飞行试验方法主要是考核卫星导航最为关键的定位精度指标。

2 系统定位精度飞行试验方法

差分卫星导航定位系统的基准设备采用定位精度同级别或更高级别的差分卫星导航系统。本文选取2套NovAtel公司的载波相位差分GPS设备，测试设备实时记录2套差分GPS输出的位置信息，采用对比法给出2套差分GPS设备间的定位相对位置误差。

2.1 不同高度平飞、爬升、下降

试飞原理：飞机在差分GPS作用下，试验机全包线范围内以不同高度做稳定平飞，平飞覆盖不同的航向；并结合飞机起飞、降落检查飞机爬升、下降条件下的定位精度。

由于卫星运行的高动态性和全球分布相对均匀特性，飞行测试可分不同时段进行，间隔时间4～6h，共飞行3～4 次。考虑通常情况下电离层对定位精度影响最大，飞行时间中需包含当地时间下午2 点，因为电离层影响在此时达到峰值[5]。

2.2 不同姿态飞行

试飞原理：试验机以不同横滚角盘旋飞行，并在安全飞行高度内检查飞机在不同仰角条件下的飞行。

试验机所处环境为空中，受地面多径效应影响较小，当试验机以不同俯仰、横滚飞行时，造成局部范围内的多径效应。并因为卫星天线遮挡能影响到卫星天线搜星数，且机载数传天线的方向性会影响到定位精度。

2.3 覆盖范围进近飞行

试飞原理：飞机从远处，在差分站数传电台有效覆盖指标范围内(通常是50～100km)朝地面差分站进近试飞。

当差分站和机载卫星接收机较近时(<20km)，公共误差部分包括卫星星历误差、星钟误差、相对论效应、电离层效应、对流层效应，这些误差对于移动站和基准站而言是高度相关的，经差分定位系统处理完全可以消除。而通常有效覆盖范围指标为50～100km，因此需考核差分站和飞机较远情况下的定位精度。

3 基于消除杆臂的数据处理

3.1 定位精度数据处理方法

根据美国联邦导航规划的规定，差分GPS定位系统水平定位精度为两倍径向均方根差(2RMS)，高度定位精度为两倍标准方差(2σ)[6]。1倍标准方差的数据处理方法可参考GJB729-89惯性导航系统精度评定方法中位置误差计算公式如下

60×1853

式中：Δλi为第i个采样时刻的经度误差(°)；Δφi为第i个采样时刻的纬度误差(°)；φi为第i个采样时刻的纬度值(°)；m为有效采样点次数。最后乘的2个常量是把以(°)表示的位置误差转换为以m为单位。

图2所示为某次飞行两部差分GPS定位结果，可以看出定位精度误差基本保持在0.2m左右，其结果与飞机的姿态角尤其是横滚角有较大关系。导致此现象出现的原因就是未对两部差分GPS安装天线间杆臂值进行补偿。

3.2 消除杆臂数据处理

杆臂效应误差是由于被试设备安装位置与基准设备安装位置不重合而引起位置输出中的附加位置误差[7-10]，它是差分GPS系统位置误差的主要误差源之一。飞机上GPS卫星天线安装相对位置一般为米级，这对于考核差分GPS定位精度来说显然不可接受。

如图3所示，OnXnYnZn为导航坐标系(n系)，ObXbYbZb为与飞机载体固连的机体坐标系(b系)。假设ObPb为2个GPS卫星接收天线在机体坐标系下的相对位置，需要将在机体坐标系下的相对位置关系通过坐标旋转变换到导航坐标系下表示成OnPn。将机体坐标系旋转到导航坐标系的转换矩阵如下

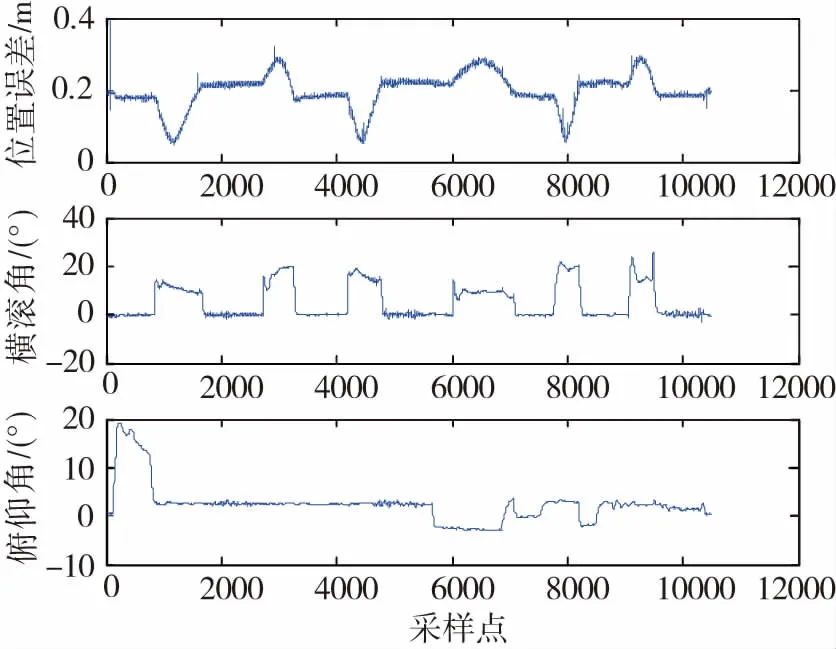
图2 飞机的横滚角、俯仰角与定位误差Fig.2 Roll and pitch angle of the aircraft and positioning error

应用上式将安装相对位置由机体坐标系(b系)转换到导航坐标系(n系)下，得到杆臂效应引起的位置误差在导航坐标系中的表达式如下

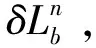
3.3 试验结果

本次差分GPS定位精度试飞测试使用的是紧凑型天线，是一种可用于飞机且外形尺寸较小的天线，天线之间安装位置为在飞机纵向偏置安装，天线振元之间相对安装位置间隔为20cm，即3.2节中的ObPb的[0 0.2 0]。经计算未消除杆臂误差前的为2RMS=0.4066m，消除杆臂误差后的为2RMS= 0.0288m，如图4所示。通过试飞测试和数据处理可以看出，2个差分GPS在平飞和不同姿态下飞行时，定位一致性较好，定位精度可以满足使用要求。

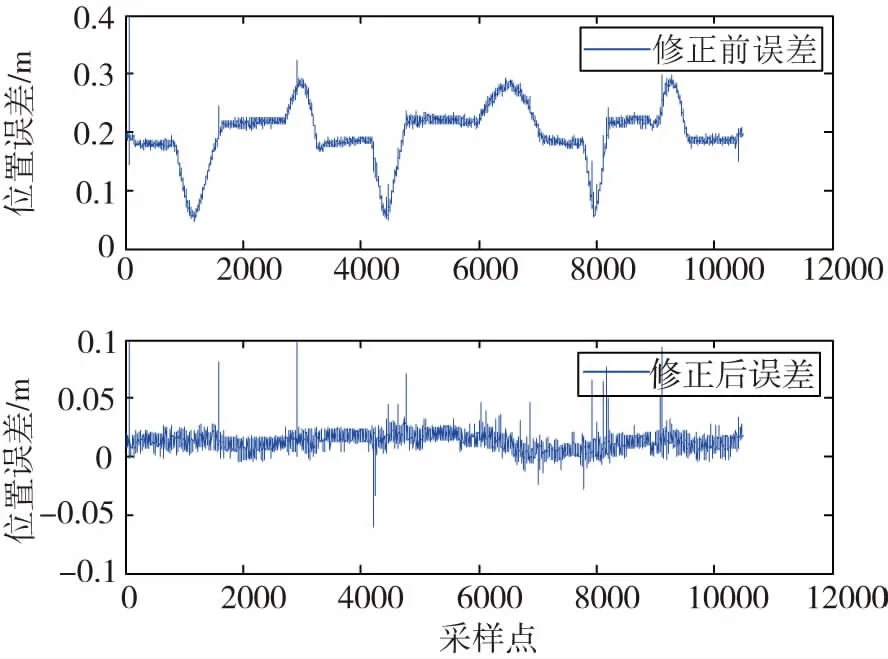
图4 消除杆臂后的定位误差结果Fig.4 The result of locating error after eliminating lever arm

4 结论

机载差分卫星导航系统的飞行测试包含定位精度、完好性、覆盖范围、信号质量等指标验证，本文针对机载差分卫星导航系统定位精度的考核，根据定位误差特性设计的试飞方法能够较好地反映出设备的真实水平，基于消除杆臂的数据处理方法可以正确地消除因为天线间安装位置不同而引入的系统误差。经过实际试飞验证方法可行，且数据处理有效。

[1] 杨杰, 张凡. 高精度GPS差分定位技术比较研究[J]. 移动通信, 2014(2):54-58.

[2] 陈树新, 王永生, 陈飞. 实时动态载波相位差分GPS定位精度分析[J]. 弹箭与制导学报, 2002, 22(3):1-5.

[3] 李斌, 王晓旺, 胡耀坤. 地基增强系统(GBAS)飞行试验分析[J]. 现代导航, 2012, 3(1):6-9.

[4] 王晓湘. 差分GPS定位精度研究[J]. 北京邮电大学学报, 1999, 22(4):25-29.

[5] 欧阳霆. 北斗卫星导航系统的飞行校验方法[J]. 中国民航飞行学院学报, 2013, 24(4):13-15.

[6] Federal Aviation Administration.United states department of transportation federal aviation administration:FAA-E-AJW44-2937A[R].Washington D.C. FAA,2005.

[7] 黄雪妮, 杨武. 飞机载体的杆臂效应对GPS测速精度的影响[J]. 导航定位与授时，2017，4(4)：57-60.

[8] 江红， 张炎华，赵忠华. 捷联惯性导航系统传统传递对准的杆臂效应分析[J]. 中国造船，2006，47(4)：71-75.

[9] Hung J C, Hunter J S, Stripling W W, et al. Size effect on navigation using a strapdown IMU[R]. USA Army Missile Research and Development Command,1979.

[10] 李江华.航空重力测量系统中杆臂效应误差补偿技术[D].长沙：国防科学技术大学，2009.