基于北斗卫星速度外推的GEO卫星速度解算方法
,,,
(北京自动化控制设备研究所,北京 100074)
0 引言
北斗二代卫星导航系统是我国自主研发、建设、维护的卫星导航系统[1],目前可以满足亚太地区的定位需求,对于我国的国防安全、信息安全与导航产业发展有着重要的意义[2]。北斗二代系统为区域系统,一期导航星座于2011年12月开始试运行[3]。截至2017年6月底,北斗二代导航系统已经具备了7颗地球静止轨道(GEO)卫星、8颗倾斜地球同步轨道(IGSO)卫星和7颗中轨道(MEO)卫星在轨正常运行、工作。为了利用有限的资源来满足亚太地区导航与定位的需求,北斗二代导航系统利用GEO卫星来保证亚太地区实时有5颗可用星,保证了北斗系统在中国的重点范围内能够应用,而且随着发射的卫星越来越多,GEO卫星可以提高在重点区域的定位、定速精度,在实际应用中有着重要意义。由于GEO卫星轨道倾角接近于0°,经典GPS广播星历参数中部分参数定义存在奇异,因此导致经典GPS广播星历参数拟合算法拟合精度降低[4]。杜兰[5]等学者基于第一类无奇点根数,分析了无旋转倾角的GEO两步法星历参数拟合算法,采用固定1~2个超限参数取值的缩减参数拟合法,取得了较好结果,但在某些时期拟合的用户距离误差较大。而现有北斗系统对其广播星历参数用户算法进行了修正,即将GEO卫星轨道坐标旋转5°。从而在经典广播星历参数用户算法的基础上提高了GEO卫星轨道的拟合精度。但这样传统的用户卫星位置计算方法不再适用于GEO卫星,需要考虑5°的人为转角[9]。文献[6]利用Chebyshev多项式拟合算法计算GEO卫星位置,但在拟合时间越过星历更新时刻时,需要多组星历,增加了计算负担,并且没有涉及卫星速度计算。文献[7]采用第二类无奇点轨道根数,避免了北斗GEO用户算法中坐标旋转处理过程,但长时间拟合位置和速度精度有所损失。文献[8]提出了一种基于卫星位置差分的GEO卫星速度解算方法,但该方法在GEO卫星变轨时运算精度较低,无法满足高精度的导航应用需求。文献[10]给出了GEO卫星的速度微分计算方法,但该方法增加了矩阵微分运算,因此运算量较大。为此,本文首先推导了GEO卫星速度的位置差分解算方法和微分解算方法,并对两种计算速度的方法做了对比,分析了两种方法的优缺点,最后提出了基于加速度补偿的GEO卫星速度外推算法。仿真结果表明:该算法在保证GEO卫星速度解算效率的前提下,提高了GEO卫星在各种复杂运动状态下的速度解算精度,具有较高的工程实践应用价值。
1 GEO卫星速度解算方法
北斗系统中GEO卫星保证了在中国区域内始终有5颗以上的可用星,地位十分重要。对其速度的解算精度也直接关系到使用者的定速精度,现一般有两种方法解算其速度。
1.1 GEO卫星速度的位置差分法
由于GEO卫星在大部分时刻运动速度较低且运动加速度较小,因此可以采用位置微分运算的方法,该方法的计算如下所示。
(1)
其中,Xk-1、Yk-1、Zk-1是上一时刻所计算出的卫星位置,Δt是两时刻之间的时间间隔。该方法的优点是运算量较低,但是该方法计算出的是卫星在2个定位时刻之间的平均速度,若是卫星加速度较大,则会引入较大的误差。
1.2 GEO卫星速度的位置微分算法
由于北斗ICD中给出了GEO卫星轨道参数的微分量,因此可以采用微分法对GEO卫星的速度进行计算。
首先计算GEO的位置如式(2)所示[11]
(2)

(3)
(4)

1)计算观测历元的偏近点角变化率
(5)
(6)
2)计算纬度幅角变化率
(7)
(8)
(9)
(10)
4)计算惯性系下卫星升交点经度变化率
(11)
5)计算卫星在自定义旋转坐标系中的速度
(12)
(13)
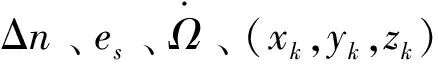
2 两种速度解算方法的对比
卫星定速时需要实时地解算卫星速度,而位置微分算法相较于位置差分算法来说更为准确,它可以解算出定位时刻所需的卫星速度,而位置差分算法解出的却是两定位时刻之间的平均速度,在卫星速度较大时,会给定速带来误差。
利用2017年3月3日的renix文件中的北斗星历,在北斗时间2017年3月2日23点—2017年3月3日23点,分别对两种方法计算的GEO卫星速度进行仿真,其中卫星位置差分的时间间隔为1s,以微分法解出的GEO速度为基准计算位置差分法的误差,结果如图1所示。

(a)地固系X向速度误差(a) Satellites velocity error of X axis in ECEF
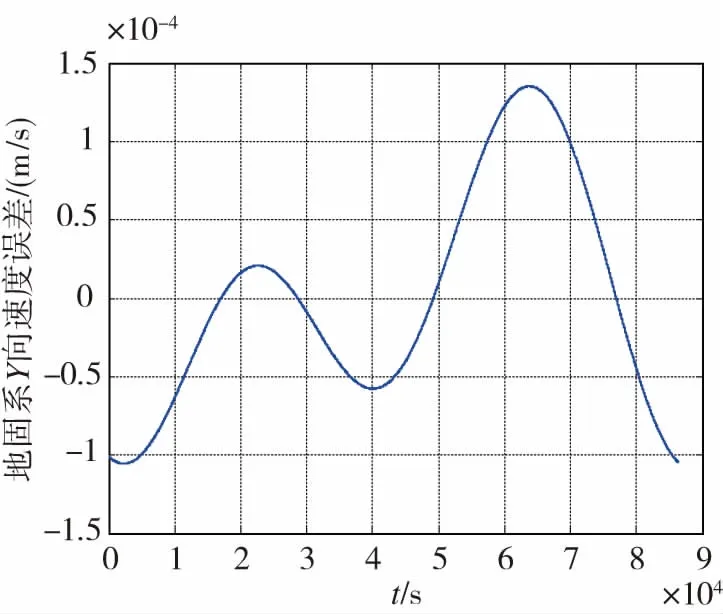
(b) 地固系Y向速度误差(b) Satellites velocity error of Y axis in ECEF

(c) 地固系Z向速度误差(c) Satellites velocity error of Z axis in ECEF图1 1号GEO卫星在地固系中速度误差Fig.1 The error of PRN 1 GEO satellites velocity in ECEF
从图1可知,在X、Y方向(ECEF系)上速度误差较小,因为GEO卫星为同步卫星,在这2个方向上的速度分量小,加速度小;Z方向误差虽然可以达到其他两方向误差的10倍,但量级依旧很小,最大只有约3mm/s的速度误差,远小于噪声对定速造成的误差,所以不会对定速造成影响。


表1 两种算法时间对比
由以上仿真可知当GEO不存在大的机动时,利用位置差分法得到的GEO卫星速度完全可以满足接收机定速的精度要求,同时该方法可以大幅降低GEO卫星的速度解算时间,降低北斗卫星导航系统的实现难度。
但是该方法的应用前提是GEO卫星轨道不存在轨道机动。轨道机动是指偏离预定轨道的卫星在发动机推力的作用下调整轨道使卫星返回到正确位置的工作[13]。轨道机动后,卫星位置变化可达数十km。其中的GEO和IGSO卫星由于其地球同步性,轨道机动比较频繁[14]。但是当GEO卫星机动发生,轨道预报将很快失效,一直到机动结束后较长时间内星历都不能有效使用,为此有众多学者研究了卫星机动期间定轨方法和机动后星历快速恢复方法,使得卫星机动期间的轨道参数精度可以接受[15]。为模拟其轨道的机动,选取一颗MEO卫星进行对GEO卫星轨道机动时的仿真,其结果如图2所示。

(a) 轨道机动时地固系X向速度误差(a) Satellites velocity error of X axis in ECEFduring orbital maneuver
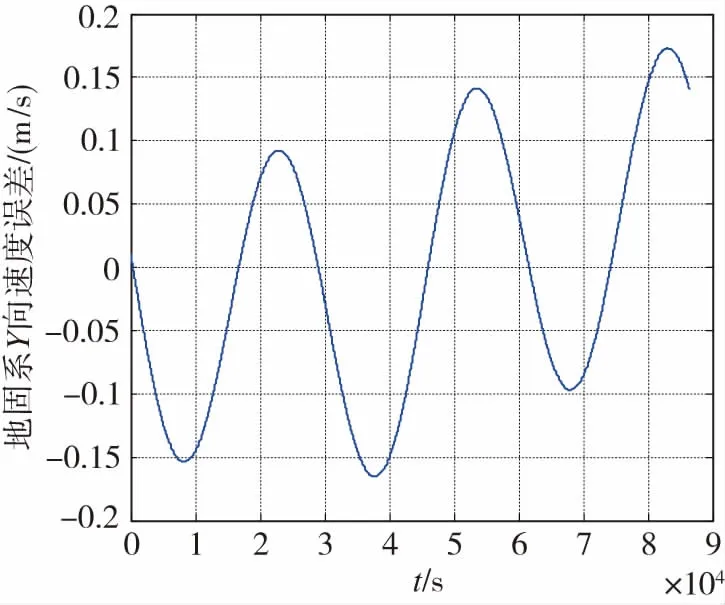
(b) 轨道机动时地固系Y向速度误差(b) Satellites velocity error of Y axis in ECEFduring orbital maneuver

(c) 轨道机动时地固系Z向速度误差(c) Satellites velocity error of Z axis in ECEFduring orbital maneuver图2 GEO卫星轨道机动时在地固系中速度误差Fig.2 The error of GEO satellites velocityduring orbital maneuver in ECEF
在轨道机动时差分算法会带来很大的卫星速度计算误差。其误差大小主要与机动时卫星的加速度大小有关。当卫星调整轨道时往往通过其内部提供推力,产生较大加速度,在较短时间内完成轨道调整。加速度与误差关系如图3所示。

图3 卫星加速度与速度误差Fig.3 Satellites acceleration and velocity error
当不考虑任何测量误差的情况下,地固系中的速度误差将直接引入到接收机所测量的伪距率中,并按视线系和地理坐标系之间的角度关系分配到接收机所输出的速度中,导致接收机的定速有一定偏差,不利于导航系统精度的提高。因此需要对这种方法进行改善。
3 基于速度外推的GEO卫星速度计算方法
由之前的分析可知,利用位置差分法虽然可以降低GEO卫星速度计算的运算量,但是若GEO卫星存在较大的变轨机动时,则现有的位置差分法计算得到的GEO卫星速度误差较大,会影响接收机的定位精度,为了在保证GEO卫星速度计算运算量的前提下进一步提高北斗卫星导航接收机的定速精度,本文提出了一种基于接收机速度外推的GEO定速方法。
若已知卫星的加速度,则可对卫星速度进行补偿。一种简单的补偿思想为视时间间隔内的卫星加速度不变,则位置差分算法计算的卫星速度实际上是2个时刻中间时的瞬时速度,可以用式(14)进行补偿,以减小速度延时造成的误差,满足高精度紧组合导航系统的应用需求。
(14)
其中,Vxdk、Vydk、Vzdk分别为位置差分算法所计算的卫星在地固系中的速度,axdk、aydk、azdk分别为位置差分算法所计算的卫星在地固系中的加速度,Vxk、Vyk、Vzk为补偿后的卫星速度,利用式(2)对时间求导计算卫星在地固系中的加速度。
(15)
(16)

(17)
其中,Vxdk -1、Vydk -1、Vzdk -1是上一周期位置差分所计算的卫星速度。为验证此种方法的可行性,在机动条件下将两种方法得到的加速度做差对比,其结果如图4所示,误差基本在10-7量级,所以用式(17)计算完全可以满足使用需求。

图4 两种方法计算卫星加速度之差Fig.4 The difference of satellites accelerationcomputed by two methods
除式(14)外,还可以用多项式拟合法、引入加加速度法等对误差进行补偿,以上方法对误差补偿有一定改进效果,但由于加加速度较小而且卫星机动的不确定性,有时也会产生更大误差,本文仅讨论式(14)的补偿方法。
4 仿真分析
利用上述算法对第2节中轨道机动时的GEO卫星速度差分算法进行补偿,仿真结果如图5所示。

(a) 补偿后轨道机动时地固系X向速度误差(a) Satellites velocity error of X axis in ECEF aftercompensating during orbital maneuver

(b) 补偿后轨道机动时地固系Y向速度误差(b) Satellites velocity error of Y axis in ECEF aftercompensating during orbital maneuver

(c) 补偿后轨道机动时地固系Z向速度误差(c) Satellites velocity error of Z axis in ECEF aftercompensating during orbital maneuver图5 补偿后的轨道机动GEO卫星在地固系中速度误差Fig.5 GEO satellites velocity error during orbitalmaneuver after compensating in ECEF
对比图2,图5中的速度误差缩小到近1/4,尤其较好地补偿了Z方向上的误差,证明了加速度补偿速度外推算法的有效性。

表2 差分法和速度外推法时间对比
两种算法执行效率相当,而补偿后的精度却可以提升约4倍以上,仿真结果证明了此算法的优越性。
由于目前接收机的输出频率通常为5Hz,所以将接收机输出的步长减小为0.2s时,使用差分法得到的轨道机动时GEO卫星速度误差如图6所示。
当接收机输出的时间间隔为0.2s时,利用速度外推法补偿后的速度误差如图7所示。

(b)轨道机动时地固系Y向速度误差(时间间隔0.2s)(b) Satellites velocity error of Y axis in ECEFduring orbital maneuver (time interval 0.2s)

(c)轨道机动时地固系Z向速度误差(时间间隔0.2s)(c) Satellites velocity error of Z axis in ECEFduring orbital maneuver (time interval 0.2s)图6 GEO卫星轨道机动时在地固系中速度误差(时间间隔0.2s)Fig.6 The error of GEO satellites velocity during orbitalmaneuver in ECEF(time interval 0.2s)

(a) 补偿后轨道机动时地固系X向速度误差(时间间隔0.2s)(a) Satellites velocity error of X axis in ECEF aftercompensating during orbital maneuver (time interval 0.2s)

(b) 补偿后轨道机动时地固系Y向速度误差(时间间隔0.2s)(b) Satellites velocity error of Y axis in ECEF aftercompensating during orbital maneuver (time interval 0.2s)
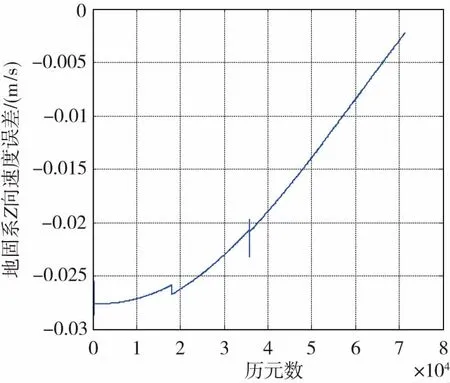
(c) 补偿后轨道机动时地固系Z向速度误差(时间间隔0.2s)(c) Satellites velocity error of Z axis in ECEF aftercompensating during orbital maneuver (time interval 0.2s)图7 补偿后的轨道机动GEO卫星在地固系中速度误差(时间间隔0.2s)Fig.7 GEO satellites velocity error during orbital maneuverafter compensating in ECEF (time interval 0.2s)
由图7可以看出,卫星位置之间的时间间隔越小,卫星速度越准确,相应的定速精度也就越高。而经过补偿的速度误差也达到了毫米量级,能够满足应用需求。
由以上仿真结果可知:本文提出的基于速度外推的GEO卫星速度计算方法在保证GEO卫星速度解算速度的前提下,提高了GEO卫星在各种复杂运动状态下的速度解算精度。
5 结论
针对现有北斗GEO卫星速度解算方法存在的缺陷,为了提高北斗卫星导航系统在各种复杂环境下的导航精度,本文在已有的GEO卫星速度解算方法的基础上提出了一种基于速度外推的GEO卫星速度计算方法,仿真结果表明:该算法在保证GEO卫星速度解算速度的前提下,提高了GEO卫星在各种复杂运动状态下的速度解算精度,具有较高的工程实践应用价值,可以有效地提高北斗卫星导航系统的应用效果。
[1] 杨秋实, 徐爱功, 祝会忠,等. BDS单参考站载波相位差分定位方法[J]. 导航定位学报, 2016, 4(4):59-64.
[2] 鲍宇. 北斗导航系统的建设与应用分析[J]. 电子制作, 2013(16):15.
[3] 中国卫星导航系统管理办公室.中国北斗卫星导航系统[R]. 2016.
[4] 刘季. 北斗GEO卫星位置计算方法探究[J]. 测绘地理信息,2012,37(5):33-36.
[5] 杜兰, 刘泽军, 周佩元,等. 无旋转倾角的NAV/CNAV型GEO广播星历拟合[J]. 测绘学报, 2017, 46(3):297-306.
[6] 欧美极. 北斗卫星导航系统的Chebyshev多项式拟合算法[J]. 中国科技信息, 2015(19):83-84.
[7] 谢小刚, 曾大治, 龙腾,等. 北斗GEO卫星用户算法的改进方法[J]. 国防科技大学学报, 2014,36(1):82-87.
[8] 刘广军, 郭晶, 罗海英,等. 北斗GEO卫星实时求速算法研究[J]. 飞行器测控学报, 2015, 34(1):57-63.
[9] Jia S, Tang X, Xiao Z, et al. Analysis of The GEO multipath impact on Ionosphere-Free Combination Positioning in BDS system[C]// 2016 IEEE International Conference on Signal Processing, Communications and Computing(ICSPCC). IEEE, 2016:1-4.
[10] 黄勇, 胡小工, 王小亚,等. 中高轨卫星广播星历精度分析[J]. 天文学进展, 2006, 24(1):81-88.
[11] 中国卫星导航系统管理办公室.北斗卫星导航系统空间信号接口控制文件[R]. 2016.
[12] Guangjun,Jing Guo. Real-time Determination of a BDS Satellite’s Velocity Using the Broadcast Ephemeris[C]//2014 4thInternational Conference on Instrumentation and Measurement, Computer, Communications and Control. 2014:478-463.
[13] 杨旭海, 李志刚, 冯初刚,等. GEO卫星机动后的星历快速恢复方法[J]. 中国科学:物理学 力学 天文学, 2008, 38(12):1759-1765.
[14] 燕兴元, 黄观文, 张睿,等. 一种基于广播星历的 BDS 轨道机动探测方法[J]. 导航定位学报, 2015,3(3):35-38.
[15] 郭睿, 李晓杰, 周建华,等. 机动力建模条件下的GEO卫星机动期间定轨[J]. 测绘科学技术学报, 2013, 30(5):465-470.
[16] 谢钢. GPS原理与接收机设计[M]. 北京:电子工业出版社, 2009:62-66.

