激光陀螺误差分析的Allan方差法改进研究

，

(1.辽宁石油化工大学 信息与控制工程学院，辽宁 抚顺 113001；2.哈尔滨工程大学 自动化学院，哈尔滨150001)

0 引言

激光陀螺的固态特性使其成为构建高精度捷联惯性导航系统的理想器件。凭借着瞬时启动快、耐冲击能力强、数字输出、工作可靠、平均无故障时间长等诸多优点[1]，激光陀螺被广泛应用于航海、航空、定位定向、陆地导航和航天火箭等领域[2-4]。作为高精度惯性器件，激光陀螺的随机误差特性是影响其精度提高的重要因素，因此，准确且有效地分析和辨识出激光陀螺随机误差中的各种噪声效应，针对各效应的影响的比重进行有效地补偿或改进，是提高激光陀螺精度的一种有效途径[5]。

Allan方差法是对激光陀螺的随机误差进行辨识与分析中被普遍采用的有效手段之一[6-7]。然而文献[8]指出Allan方差法没有包含导航用的零偏不稳定性项，并通过经典方差法与Allan方差法之间的恒等关系指出角速度随机游走项和速率斜坡项均为负值，且量化噪声项也有负值情况出现的可能，而这与方差为正值的思想相悖。因此需以经典方差法来评价激光陀螺的性能。文献[9]采用阻尼振荡的思想建立功率谱密度的数学模型，最终通过建立经典方差法的拟合公式来完成漂移项的估计，解决了上述Allan方差法在分析过程中存在的不足，但经典方差法的拟合精度要比Allan方差法的拟合精度差。文献[10-12]提出的动态Allan方差法能够全面和准确地评价陀螺的性能，由于动态Allan方差法是由Allan方差法通过窗口截取得到的，其本质是三维的Allan方差表现形式，所以Allan方差法中存在的诸多不合理之处都会直接引入到动态Allan方差法中。

为此，本文将阻尼振荡法的分析思想和模型引入到动态Allan方差法中，建立了改进动态Allan方差法的数学模型，并通过改进Allan方差法对实际测量激光陀螺数据的误差特性进行了辨识与分析，仿真和分析结果验证了改进动态Allan方差法的正确性和有效性。

1 阻尼振荡形式的随机漂移模型

阻尼振荡形式的随机漂移模型是将噪声项假设为各种阻尼振荡形式，推导出其功率谱密度，并将其与量化噪声项的功率谱密度结合起来形成随机漂移的功率谱密度表达式，经傅立叶逆变换后，得到时域上的经典方差表达形式：

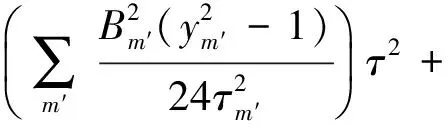
(1)

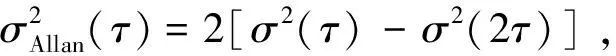
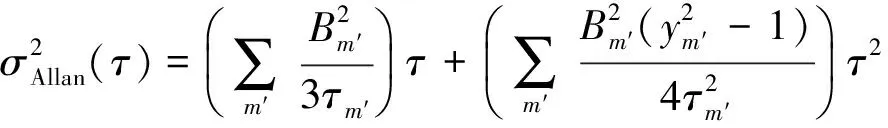
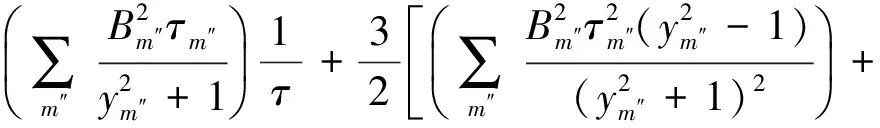
(2)

式中，m′代表慢漂类阻尼振荡，m″代表快漂类阻尼振荡，m代表不快不慢漂类阻尼振荡。文献[13]对此已经给出了详尽的定义及推导过程，本文在此便不再赘述。

式(1)和式(2)也可以分别简化为如下所熟知的表达形式：

(3)

(4)

对比式(3)和式(4)可以看出，式(4)的慢漂项中缺少了a0项，此项是由1/f噪声引起的，通常称之为零偏不稳定性项，传统Allan方差法并非缺少对此项的估计，而是在采用阻尼振荡法之后，由经典方差法表达式转化Allan方差法表达式的过程中，此项中不包含相关时间而最终被消去。对于整个误差项的估计需通过经典方差法辅助Allan方差法来完成。实际上，只需完成经典方差法的参数估计，再通过式(3)与式(4)之间系数的关系直接计算出精细的Allan方差法的各项系数，可省去对Allan方差法的估计过程。

在传统Allan方差法中，各误差项的方差为正值，因此，要求各误差项均大于零。而采用阻尼振荡形式的随机漂移模型只要求这三类漂移分别大于零，而并未要求每类漂移中所包含的子误差项均大于零，这便巧妙地避开了传统Allan方差法中的量化噪声项、角度随机游走项和速率斜坡项出现负值却无法给出合理解释的情况。

由经典方差法推得的Allan方差的拟合精度略逊于传统的Allan方差法[8]。相比传统Allan方差法，动态Allan方差法的拟合结果又更为精确些。所以，本文将阻尼振荡法的经典方差模型引入到动态Allan方差法之中，用以提高拟合结果的精细程度。

2 基于动态Allan方差的改进Allan方差法

动态Allan法是Allan方差法的三维表现形式，能够体现出惯性器件的瞬时稳定性[14-15]，它的一个突出优点就是能够体现随机误差的非平稳性变化。在动态Allan方差法中，通过一个以给定时刻t1为中心点，长度为T的矩形窗口来截取数据进行Allan方差估计。然后窗口滑动到下一中心时刻t2，估计这一时刻矩形窗口数据的Allan方差。需要注意的是相邻两时刻的矩形窗口须有交叠部分。如此反复地进行此项工作就能够观察出代表随机误差的Allan方差随时间增长而不断演变的过程，这也就是动态Allan方差法的形成过程。而改进Allan方差法的形成过程与动态Allan方差法的形成过程是一致的，只是对窗口截取数据的Allan方差估计采用经典方差法的式(3)来完成，其推导过程如下。

考虑连续时间的数据测量，假设x(t)为激光陀螺输出的随机误差数据。可以使用窗口区间为t-T/2≤t′≤t+T/2的矩形窗口PT(t′)对随机误差数据x(t′)进行截取，截取得到的数据为

xT(t,t′)=x(t′)PT(t-t′)

(5)

式中，xT(t,t′)就是截取所得的数据。长度为T的矩形窗口PT(t)有如下的定义形式：

(6)

对于任意一个窗口来说，时刻t是一个固定的参数，它代表着分析窗口PT(t-t′)的中心。t′代表着窗口内流失的时间。由式(3)可得到t′时间内经典方差的估计窗口Aτ(t′)，通过截取的数据和Aτ(t′)进行卷积运算可建立一个增量过程Δ(t,t′,τ)。

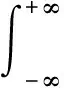
(7)

式中，各变量的约束条件如下：

(8)

t-(T/2-τ)≤t′≤t+(T/2-τ)

(9)

0<τ≤τmax

(10)

其中，τmax是经典方差估计窗口内数据的最大的观测时间间隔，可以选为

τmax=T/3

(11)

经典方差法的实质是先对一组陀螺输出信号求取均值，通过陀螺输出信号与均值作差，得到的差值序列即被认定为随机误差，最后对随机误差序列平方的总体取均值，其简化形式可写成

(12)

式中，Δ(tk,τ)就是tk时刻，相关时间为τ时的随机误差。符号<·>代表对时间序列的总体取均值。

将式(7)中的增量过程代入式(12)，可得

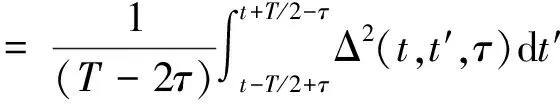
(13)

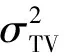
=E[<Δ2(t,t',τ)>]

(14)

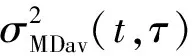
(15)

此外，需要指出的是选择不同的分析窗口类型可以有效地改进其性能，例如选择海明、汉宁、高斯或者三角窗口等。本文旨在对阻尼振荡形式的动态Allan方差法进行验证与分析，因此，本文中仅采用了单一的矩形分析窗口，而并未过多地对其他窗口进行深入研究。但若需进一步提高改进动态Allan方差法的表现性能，窗口的选择是后续值得进一步深入研究的。

3 激光陀螺零偏数据的误差特性分析

本文对实验室内现有的某型激光陀螺的零偏数据进行了实际测量。并分别采用了基于阻尼振荡的Allan方差法和改进动态Allan方差法对采集的激光陀螺零偏数据进行了辨识与对比分析。

试验数据采集过程中，将激光陀螺固定在静止的速率转台之上，由速率转台为其提供一个水平基准。采样时间为10多个小时，采样频率为1Hz。采样得到的激光陀螺数据如图1所示。

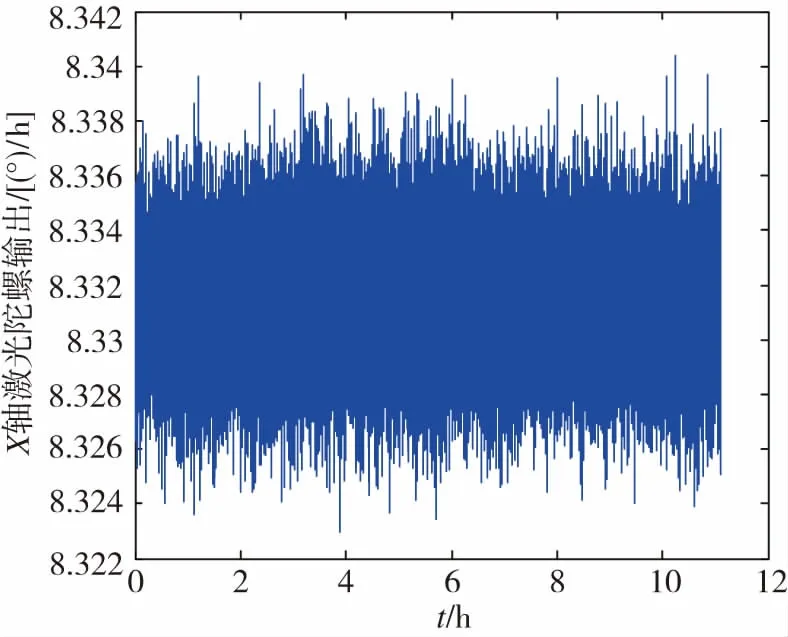
图1 X轴激光陀螺输出Fig.1 The output of X axis Laser gyro

对采集的数据进行功率谱密度分析，功率谱密度的低频和高频部分分别如图2和图3所示。

从低频部分图2中可以估计出频带的弛豫时间τm为1个多小时，较采样周期τ大很多，即τ/τm≪1，因此可以看作慢漂类漂移。因此在式(3)中应包含慢漂类漂移。而从高频部分图3中可以看出，激光陀螺的零偏数据中只含有快漂类漂移，而不含有不快不慢类漂移。所以对此次采集的激光陀螺零偏数据的误差项估计应采用下面的经典方差拟合公式。

(16)

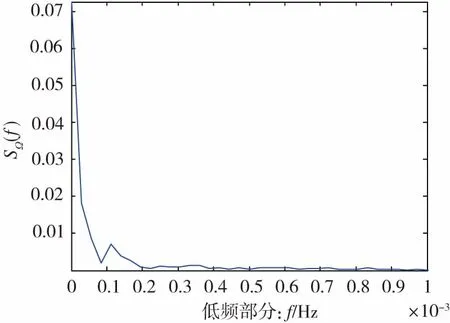
图2 激光陀螺输出数据的低频部分Fig.2 Low frequency part of the laser gyro output data

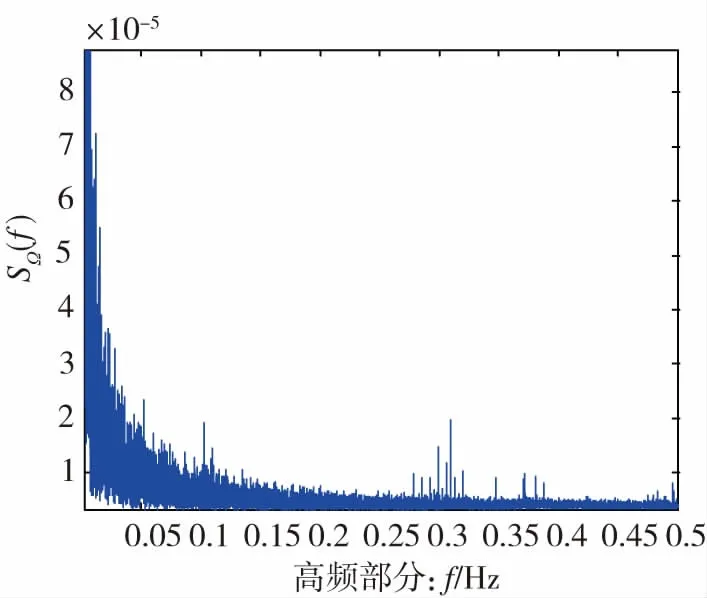
图3 激光陀螺输出数据的高频部分Fig.3 High frequency part of the laser gyro output data

设定改进Allan方差法的矩形窗口长度T为3600s。由式(16)可以得到激光陀螺数据的Allan方差法和改进Allan方差法的曲线拟合结果如图4和图5所示。图4中红色曲线为激光陀螺输出零偏数据的Allan方差曲线，蓝色曲线为其拟合曲线。

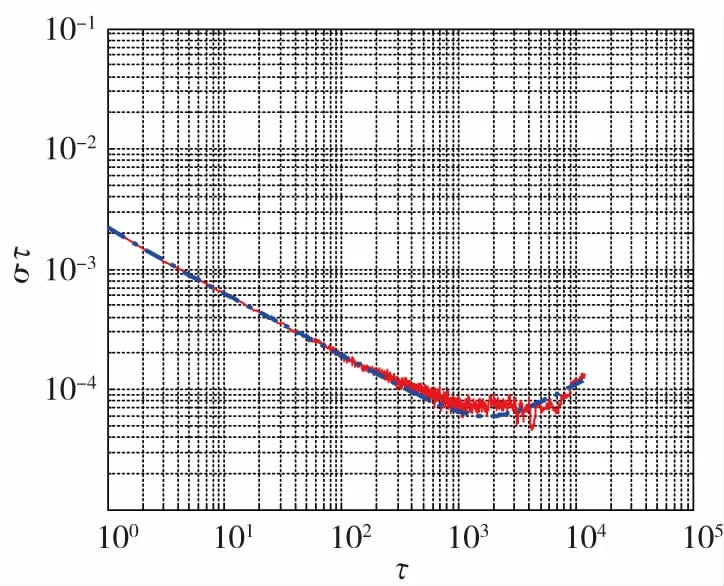
图4 基于阻尼振荡法的Allan方差双对数拟合图Fig.4 Double logarithmic fitting of Allan variancebased on damped oscillation method

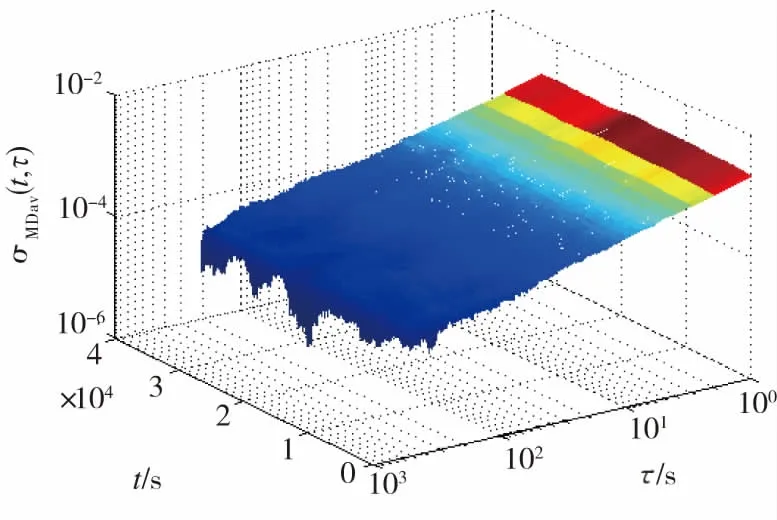
图5 激光陀螺输出数据的改进Allan方差曲线Fig.5 Improved Allan variance curve of laser gyro output data

由上述两种方法的拟合结果得到的快漂项和慢漂项及其展开得到的各子误差项的结果如表1所示。

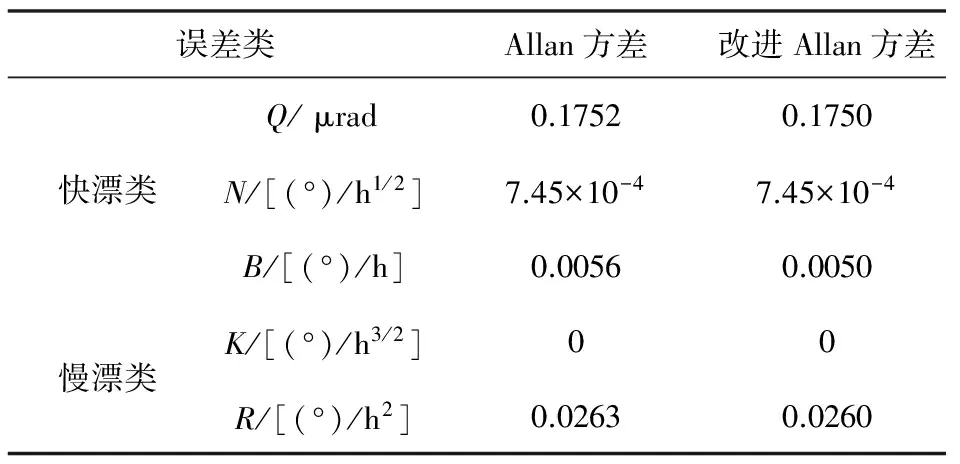
表1 两种分析方法辨识结果的对比

表1中的Q、N、B、K和R分别为激光陀螺的量化噪声项、随机游走项、零偏不稳定性项和角速率随机游走项和速率斜坡项。Allan方差法是由经典方差法经恒等关系式推导出来的，其误差项直接由辨识系数经单位转换得到，而改进动态Allan方差法的误差项是由拟合后得到的经典方差系数a0～a4经式(4)得到Allan方差系数，再由Allan方差系数经单位转换得到的。表1中的K项的辨识结果均为零，说明在此激光陀螺输出的零偏信号中不存在马尔科夫过程。N项和B项都很小，说明该激光陀螺的谐振腔的品质较高。

在对表1结果的整体对比中可以看出，Allan方差法与改进Allan方差法辨识出的快漂类和慢漂类漂移结果基本保持一致，只是在部分误差项的辨识结果中，改进动态Allan方差法的辨识结果显得更为精细些。这是因为DAVAR是由多个固定长度的Allan方差所组成的，其拟合结果为多个Allan方差的拟合结果的平均，反映的是多次计算所得的各误差系数的平均水平。因此，在随机信号为平稳信号的情况下，改进动态Allan方差法的辨识结果就显得更为精确些。

改进Allan方差法的另一个优势是从它的分析图中能够观察出随机信号受污染的情况，特别是受温度、湿度等环境干扰的情况。从图5中可以看出，该随机信号是较为平稳的，受环境影响较小。

为了进一步说明改进Allan方差法对非平稳信号的分析能力。本文通过温箱控制激光陀螺的工作环境温度变化，采集了近30h的激光陀螺零偏数据，为了提高改进Allan方差法的运行效率，对采集的激光陀螺零偏数据进行了百秒平滑，平滑后的结果及温箱温度变化情况如图6所示。

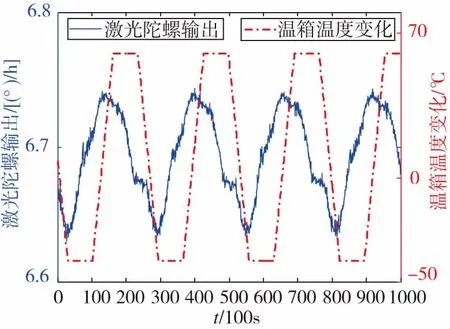
图6 变温环境采集的激光陀螺数据Fig.6 Laser gyro data collected in achanging temperature environment

由于图6中的激光陀螺输出信号为非平稳信号，而Allan方差法只能对平稳信号进行辨识，因此本文仅给出了改进Allan方差法的辨识结果。设定矩形窗口长度T为330，得到变温环境下的激光陀螺零偏数据的改进Allan方差如图7所示。

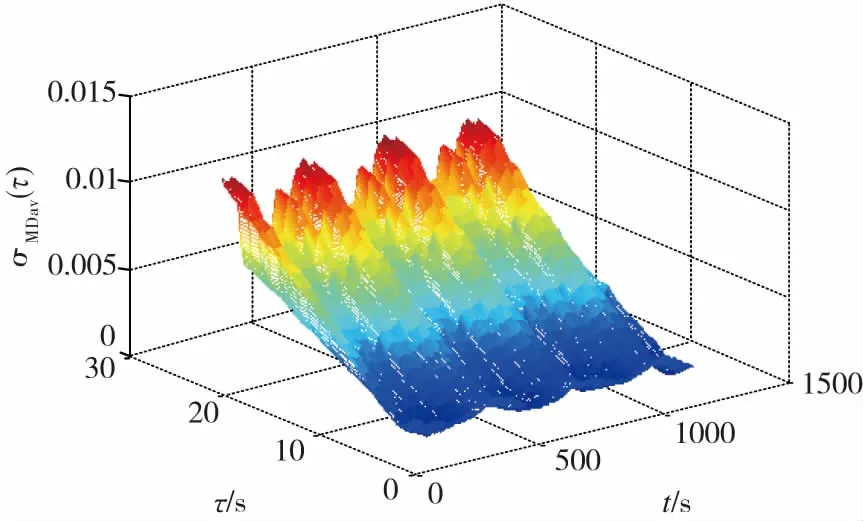
图7 变温环境下激光陀螺数据的改进Allan方差图Fig.7 Improved Allan variance curve for laser gyrodata in changing temperature environment

从图7中可以很清晰地看出动态误差信号随时间发生的周期性变化，即该方法能够表现出激光陀螺的随机误差特性受温度影响而变化所体现出的时变特性。因此，从上述对改进Allan方差法的辨识和分析结果中可以看出，改进Allan方差法对激光陀螺的误差特性进行辨识与分析是有效和可行的，不仅能够对激光陀螺输出的平稳信号进行辨识与分析，还能够完成在变化环境下所采集到数据的非平稳信号分析。

4 结论

传统Allan方差法对各误差项的分析存在不足，而阻尼振荡方法在对各误差项的分析较为合理，但其通过经典方差法拟合的结果导致拟合精度稍差。因此，本文在阻尼振荡法的基础上引入了动态Allan方差法，将阻尼振荡模型与动态Allan方差法模型结合起来进行改进，并给出了改进Allan方差法的具体推导过程。通过实测的激光陀螺零偏数据对Allan方差法和改进Allan方差法进行了辨识结果的对比和分析。分析结果验证了改进Allan方差法的有效性和可行性。通过对变温环境下的激光陀螺零偏数据进行对比分析可知，改进Allan方差法同时具备平稳信号和非平稳随机信号的处理分析能力。

[1] 唐百胜，江腾飞. 基于贝叶斯理论的激光陀螺可靠性评估[J]. 导航与控制，2016,15(2): 51-56.

[2] 周冉辉. 舰用高精度激光陀螺惯导内杆臂误差分析及补偿方法研究[J]. 舰船科学技术，2016,38(7): 120-123.

[3] 杨建强，刘灿，尹中锋，等. 激光陀螺定位定向系统工作模式机理分析[J]. 激光与红外，2017,47(3): 332-336.

[4] 李龙，梁可，陈林峰，等. 基于菲涅尔透镜的零闭锁激光陀螺抗辐照方案[J]. 中国惯性技术学报，2017,25(1): 115-118.

[5] 李汉舟. 基于激光捷联惯导的实时高精度动态姿态测量系统研究[D]. 西安: 西北工业大学，2015.

[6] 杨鸿波，臧强，高晶敏，等. 四频差动激光陀螺随机误差建模与滤波研究[J]. 压电与声光， 2015,37(4): 558-560.

[7] 魏建仓，郭岳山，刘东娜. 船用光学陀螺动态随机误差特性分析方法[J]. 水道港口，2016,37(6): 657-662.

[8] 张梅, 张文. 激光陀螺漂移的研究方法(一)[J]. 中国惯性技术学报, 2009,17(3): 210-213.

[9] 张梅, 张文. 激光陀螺漂移的研究方法(二)[J]. 中国惯性技术学报, 2009,17(3): 350-355.

[10] 魏国, 龙兴武. 基于动态Allan方差的机抖激光陀螺随机误差研究[J]. 中国激光, 2010,37(12): 2975-2979.

[11] 张谦，王玮，王蕾，等. 基于动态Allan方差的光纤陀螺随机误差分析及算法改进[J]. 光学学报，2015,35(4): 57-63.

[12] 汪立新，朱战辉，李瑞. 动态Allan方差改进算法及其在FOG启动信号分析中的应用[J]. 红外与激光工程, 2016 , 45(7): 261-268.

[13] 高伯龙, 王关根. 陀螺数据的数学处理[J]. 国防科学技术大学学报, 1979(1): 91-106.

[14] Galleani L， Tavella P. The dynamic Allan variance V: recent advances in dynamic stability analysis[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2016,63(4): 624-635.

[15] Draganová K， Moucha V， Volěko T, et al. Non-stationary noise analysis of magnetic sensors using Allan variance[J]. Acta Physica Polonica A, 2017,131(4): 1126-1128.