一种多操纵面复合控制的动态分配策略研究

，，，

(北京控制与电子技术研究所，北京 100038)

0 引言

传统大气层内飞行器的控制指令与舵面偏转角的对应关系是明确的，控制分配策略是唯一的。近年来随着新型飞行器的不断涌现，有些飞行器为增加系统容错能力，采取多操纵面复合控制方式，由于气动舵面冗余，控制指令与舵面转角关系不再是一一对应的，控制分配策略也不再唯一，如何有效地将控制指令分配到各操纵面也成为姿态控制系统设计必须考虑的问题。

多操纵面的飞行器控制系统可以认为是一种过驱动系统，在数学上多操纵面分配问题可以描述为一种包含约束条件的过驱动系统分配问题。针对该类问题，一般的方法是将控制律与分配律作为2个独立的模块进行设计和分析。由控制律模块得到虚拟控制量，分配律模块将虚拟控制量分配到不同的操纵面，形成真实的控制量。美国在20世纪90年代中期开始控制分配研究，道格拉斯宇航中心在F-15 Active主动控制技术验证机上进行过多操纵面控制分配技术研究；怀特试验室的研究人员在带推力矢量的F-16上验证了基于伪逆法的控制分配算法[1]。目前多操纵面控制分配技术研究成果已经在有人驾驶飞机F-22和F-35B，以及无人机X-45B和X-48B/C上得到了初步应用[2]。

控制分配律普遍采用的方法包括广义逆法、链式递增法、直接分配法、线性规划法以及动态控制分配方法等，但这些方法大多是针对单目标优化问题[3]。对于多操纵面复合控制问题，一般是多目标与多约束条件的问题。针对多目标优化问题，要想求得某个解使得所有目标函数均达到最小一般是不可能的，一般通过加权组合转化成单目标优化问题，获得使各个目标函数都尽可能小的最优解[4]。但对飞行器而言，不同飞行阶段各目标之间的重要性也会有所差异，因此有必要根据飞行状态不断调整目标函数[5]。针对多约束问题，特别是含有舵面摆角受限等不等式约束，无法直接应用拉格朗日乘子法求解的情况，比较流行的处理约束条件优化的方法为罚函数方法。罚函数将一个有约束优化问题转化为单个的无约束极小化问题，能最有效地应用比较成熟的无约束优化的成果来求解有约束优化问题[6-10]。

此外，从工程实现角度出发，希望控制系统具有较小的质量，而执行机构的质量与功率直接相关，因此为减小系统质量，需要降低对执行机构最大功率的需求。由于多操纵面的执行机构在舵效、负载等方面均存在差异，操纵面分配结果会影响执行机构的功率需求。若控制分配不合理，当姿态控制系统功率需求较大时，可能会使某一执行机构功率需求超过其最大功率，导致执行机构失控，进而影响姿态控制系统的稳定性。反之，如果对控制分配策略进行优化，也可以减小系统的最大功率需求，在保证系统稳定的情况下实现减重。因此，可以将执行机构的功率需求作为控制分配目标函数的内容。

本文针对某飞行器多操纵面复合控制问题，构造了适应执行机构多约束与功率最优的目标函数，根据飞行状态动态调整目标函数，得到能够适应不同飞行状态的多操纵面复合控制动态分配策略。

1 控制分配问题描述

以单通道为例，飞行器操纵过程中，姿态控制模块输出虚拟控制量u(t)∈R，对应控制力矩需求为Mc(t)=k·u(t)，k为虚拟控制量与控制力矩之间的比例系数；操纵面偏转量为δ(t)∈Rm，这里m>1。通过控制分配模块，确定δ(t)以满足式(1)

B(t)δ(t)=Mc(t)

(1)

其中,B(t)=[b1(t),b2(t),…,bm(t)]为1×m的控制效率矩阵。

控制系统结构图如图1所示，虚线框内为控制分配部分，分配律设计的目的是合理分配各操纵面的指令，使得各操纵面产生的合力矩等于控制需求的力矩。为简化问题，这里将忽略各操纵面之间的气动耦合效应。

与此同时，控制分配也需要满足执行机构的位置约束与速度约束，则控制分配的多目标分配方法可用式(2)来描述。

min[f1(δ),f2(δ),…,fn(δ)]T(n≥1)

(2)

s.t.B(t)δ(t)=Mc(t)

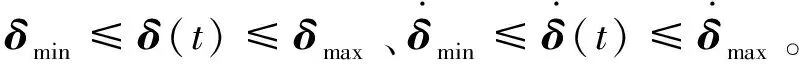
2 飞行器模型

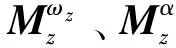
(3)

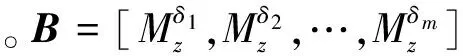
为简化分析，本文仅研究俯仰通道姿态控制分配问题，俯仰通道动力学与运动学方程如式(4)所示，式中φ为俯仰角。

(4)

操纵面执行机构功率如式(5)所示，式中P=[P1,P2,…,Pm]T为功率向量，Mjl=diag(Mjl_1,Mjl_2,…,Mjl_m)为铰链力矩矩阵。

(5)

为方便分析，假设铰链力矩与操纵面摆角成正比，如式(6)所示，式中mjl=diag(mjl_1,mjl_2,…,mjl_m)为铰链力矩系数矩阵，q为飞行动压。

Mjl=mjlδq

(6)

3 构造目标函数

为确定控制分配的策略，首先要明确控制分配中的多目标函数。虽然控制分配不影响稳态控制量的大小，但由于各操纵面的动态特性与舵效存在一定差异，导致控制分配会影响控制回路的过渡过程，因此有必要将控制分配实现的快速性作为目标函数的一部分。控制分配同样会影响对执行机构的功率需求，因此把功率需求也作为控制分配目标函数的一部分。

由于舵效存在差异，控制分配时不能直接进行舵面分配，而必须按控制力矩进行分配。设分配关系如式(7)所示。

(7)

以分配系数为状态量，将多目标函数通过加权合成形成单目标函数。这里取目标函数如式(8)所示。该目标函数前第一项使得各操纵面都尽量小，避免了由于某一操纵面分配的控制量过大而导致该操纵面运动时间过长。同时该目标函数恰好可以作为式(2)中不等式约束的罚函数，将不等式约束转化为目标函数。

(8)

由此，只要确定式(8)所示目标函数中加权系数矩阵w的增广矩阵，便可由拉格朗日乘子法进行控制分配计算。

在实际工程中，应尽量避免出现任何舵面饱和情况，因此本文在确定加权系数时考虑了最大摆角范围。这样可以在多操纵面控制能力足够时，任一操纵面均不出现饱和情况；而在多操纵面控制能力不足时，多操纵面同时饱和。如果出现多操纵面同时饱和情况，说明控制力不足，不属于控制分配解决的问题。对于功率项加权系数，通常而言，执行机构功率与飞行动压密切相关，因此加权系数考虑与动压相关。具体加权系数如式(9)所示。

(9)

式中，qmax为最大飞行动压，q≤qmax。这种加权分配方法，对飞行状态具有自适应能力：当飞行动压较小时，对执行机构功率需求较小，目标函数第一项起主要作用，即主要通过控制分配保证系统的动态特性；当飞行动压较大时，目标函数第二项起主要作用，即保证系统总功率较小。

4 控制分配策略

由式(8)与式(2)中等式约束，可写出拉格朗日函数如式(10)所示。

λ1(B(t)δ(t)-Mc(t))

(10)

求解拉格朗日的极值的必要条件为

(11)

求解式(11)即可求得控制分配矩阵k=[k1,k2,…,km]T。

5 数学仿真验证

设飞行器两种气动舵面摆角范围分别为：δ1∈[-20°,20°]，即δ1max=20°；δ2∈[-10°,10°]，即δ2max=10°。两种舵的控制力矩与铰链力矩随舵面摆角变化曲线如图2与图3所示，δ2的控制力矩与铰链力矩相比δ1都要大。

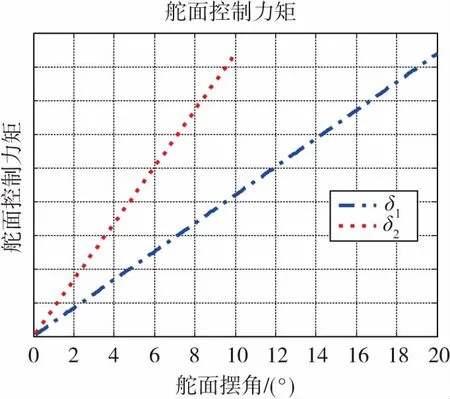
图2 控制力矩Fig.2 Control moment

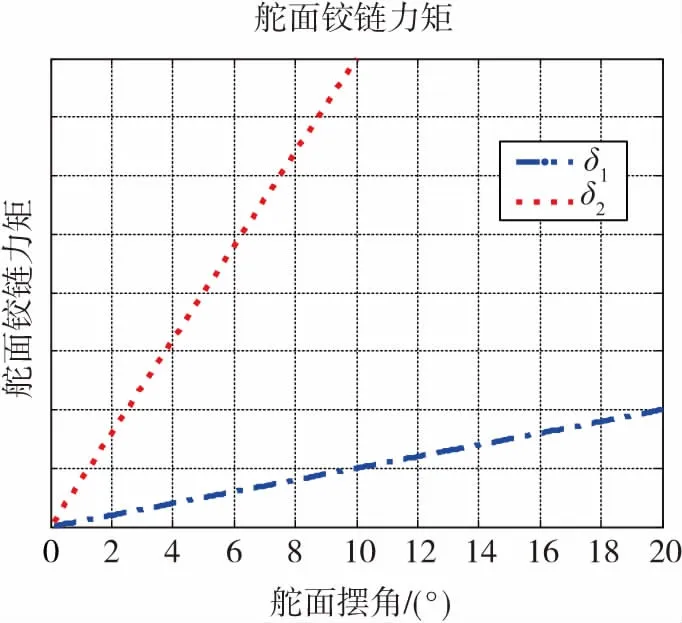
图3 铰链力矩Fig.3 Hinge moment

飞行动压变化曲线如图4所示，在40s内由10万Pa增加到50万Pa。

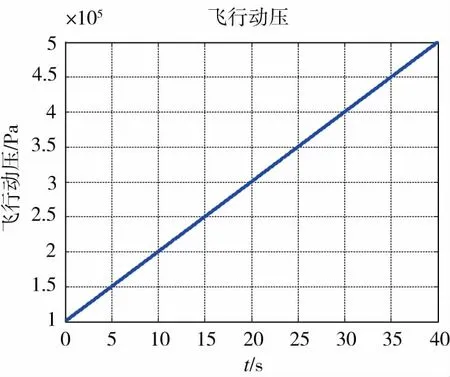
图4 飞行动压Fig.4 Flight dynamic pressure

数学仿真中，俯仰角指令为正弦指令，仿真曲线如图5～图8所示。

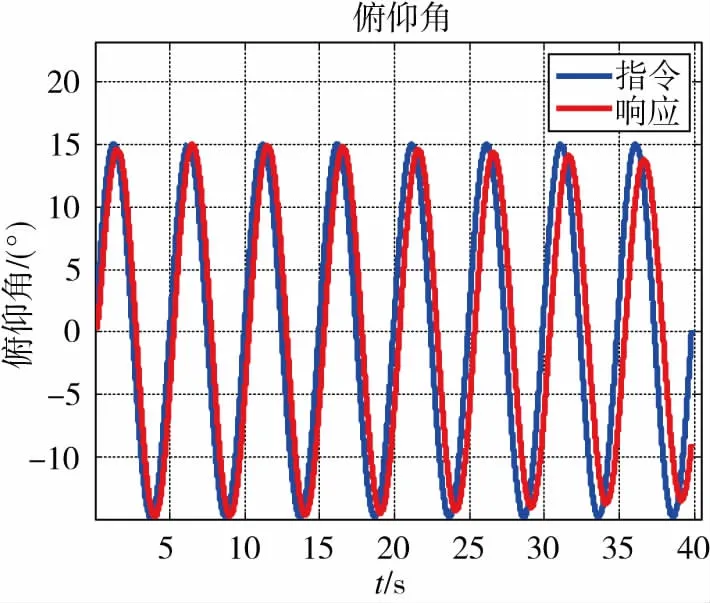
图5 俯仰角跟踪曲线Fig.5 Pitch tracking curve

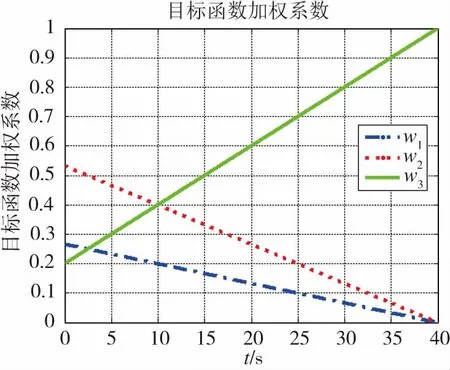
图6 目标函数加权系数Fig.6 Weighted coefficient of objective function

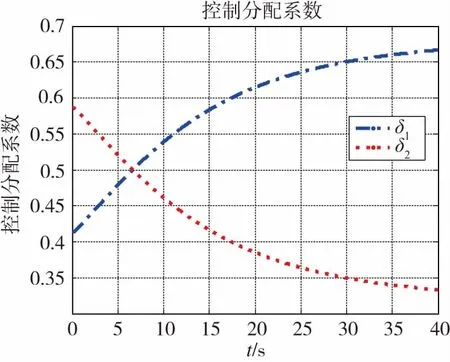
图7 舵面分配系数Fig.7 Rudder partition coefficient

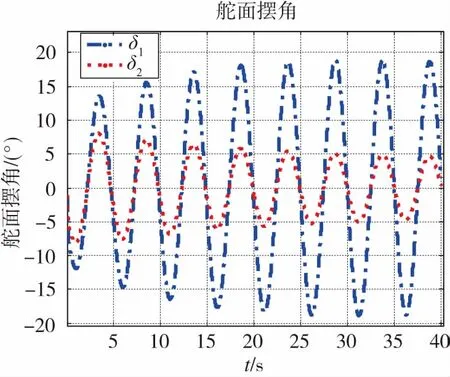
图8 舵面摆角Fig.8 Rudder angle

为考核该方法对执行机构功率的优化效果，对固定分配比例与本文的多目标自适应加权最优分配策略数学仿真结果进行对比，如图9与图10所示。本文采用的方法，在功率需求小的飞行阶段，执行机构输出合功率相对较大，以满足动态特性要求；而在对功率需求较大的飞行阶段，执行机构输出合功率则相对较小。

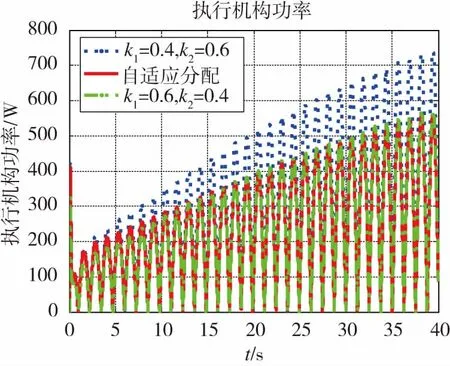
图9 执行机构功率Fig.9 Actuator power

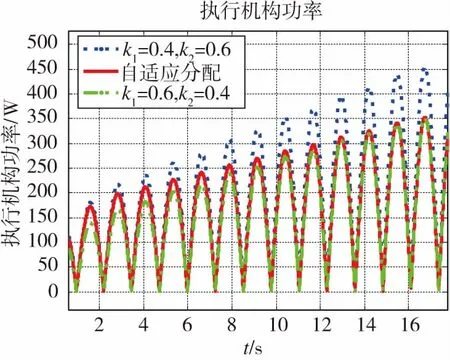
图10 执行机构功率(局部)Fig.10 Actuator power (local)

6 结论

本文针对多种控制舵面复合控制的控制分配策略问题，综合考虑不同操纵面的执行机构在摆角范围、舵面效能、负载特性等多个方面的差异，设计了一种多目标自适应动态加权最优分配策略，有效地处理了不同性能操纵面之间的控制分配问题，并通过数学仿真对比试验，验证了该分配策略的有效性。通过本文可以得到以下两点结论：

1)采用多种控制舵面进行复合控制，可将舵面的不等式约束通过罚函数方式构造目标函数，并采用拉格朗日乘子法求得最优控制分配。

2)结合飞行状态的自适应动态加权方法确定目标函数，可以进一步提升控制分配策略的整体性能。

[1] 占正勇, 刘林. 多操纵面先进布局飞机控制分配技术研究[J]. 飞行力学, 2006, 24(1):13-16.

[2] 屈晓波. 无尾飞翼飞机多操纵面控制分配技术研究[D]. 西安: 西北工业大学, 2015.

[3] 姚从潮, 王新民, 陈晓,等. 基于改进多目标遗传算法的再入飞行控制分配研究[J]. 西北工业大学学报, 2014，32(2):315-322.

[4] 杨恩泉, 高金源, 李卫琪. 多目标非线性控制分配方法研究[J]. 航空学报, 2008, 29(4):995-1001.

[5] 柳扬, 安锦文. 多操纵面战斗机动态控制分配策略研究[J]. 火力与指挥控制, 2009, 25(5):134-137.

[6] 楼烨, 何志华, 陈宝冲. 带有不等式约束的全局最优性条件[J]. 应用数学与计算数学学报, 2004, 18(1):57-62.

[7] 蔡海鸾. 惩罚函数法在约束最优化问题中的研究与应用[D]. 上海: 华东师范大学, 2015.

[8] 李丽荣, 刘春生, 韩璞. 基于智能控制的多操纵面飞行器控制分配研究[J]. 计算机仿真, 2016, 33(6):19-22.

[9] 张之瑶, 黄万伟, 柳嘉润. 一种基于自适应控制分配的飞行控制方法[J]. 航天控制, 2014, 32(3):23-28.

[10] 宋筱祺, 刘春生, 李丽荣. 基于蚁群优化的多操纵面战斗机控制分配策略[C]// 第33届中国控制会议. 南京, 2014: 8657-8660.