大跨径混凝土斜拉桥线形优化预测研究

于景飞，吴炎奎，苏醒



大跨径混凝土斜拉桥线形优化预测研究

于景飞1，吴炎奎1，苏醒2

(1. 内蒙古科技大学 土木工程学院，内蒙古 包头 014010；2. 河南省公路工程局集团有限公司，河南 郑州 450009)

大跨径混凝土斜拉桥施工工序复杂，施工过程中受到诸如拉索垂度、温度变化、混凝土收缩徐变效应等非线性因素影响，使立模标高的设定存在较大误差，理想的成桥状态难以实现。为使成桥线形准确，结构受力均衡，综合分析影响施工立模标高的因素，建立基于粒子群优化算法的BP神经网络立模标高修正参数的预测模型，对修正值进行预测。研究结果表明：所建模型性能稳定，具有较好的预测泛化能力。由预测结果得到的线形更接近理想成桥线形，主梁结构受力合理，能够实现较好的成桥状态，为斜拉桥主梁线形优化方法提供参考。

立模标高；斜拉桥施工；粒子群算法；神经网络；线形优化

斜拉体系桥梁为柔性超静定结构，构造较为复杂，而成桥线形作为施工控制的重点存在着施工过程所处状态与理想状态难以吻合的问题，其中立模标高参数的确定直接影响着整个结构成桥线形的实现，因此对立模标高参数的预测修正具有理论意义和应用价值。时至今日，现代工程控制理论和方法不断发展，一些误差优化预测方法在各工程领域得到应用并取得了一定的控制效果。刘建威等[1]运用改进灰色GM法对高速公路路基沉降进行预测。崔雍等[2]运用层次分析法与神经网络理论进行有效结合，快捷预测了桩基承载力。陈治亚等[3]将改进的BP神经网络模型运用到物流需求规模预测，效果显著。在桥梁施工方面，林元培[4]运用Kalman滤波法逐步计算索拉力调整值进行施工控制。陈建阳等[5]用神经网络方法预测桥面预拱度误差值。斜拉桥结构自身具有特殊性，施工中索力和线形控制相互影响，而卡尔曼滤波的方法是将误差不断累积到索力中，通过调整索力来消除误差，这样对拉索的调控和受力不利。标准BP神经网络也有着逼近速度慢，在训练过程中很难跳出局部最优解等缺点，影响整个网络的泛化能力，也不能得到理想的预测结果。基于此可以考虑在BP神经网络模型的基础上引粒子群算法，优化网络结构，以提高网络的预测性能[6−7]。本文以河南武云高速大跨径独塔PC斜拉桥为工程依托，将优化后BP神经网络预测模型引用到斜拉桥施工中线形优化控制上，建立了立模标高修正值的预测模型，分析该模型的优化方法并进行预测输出，取得了较好的预测结果，为大跨径混凝土斜拉桥成桥线形优化方法提供参考。

1 线形控制原理模型

在桥梁施工中常用自适应控制法对施工过程进行控制。即主动地对主梁标高和索力的实测值与理论值的误差进行分析，对影响桥梁有限元计算模型的重要计算参数进行辨识，并通过对计算模型参数偏差的修正，重新进行模型的分析计算，使计算结果与实测结果相符，以指导当前施工，实现线形控制的目的。线形控制原理模型如图1所示。

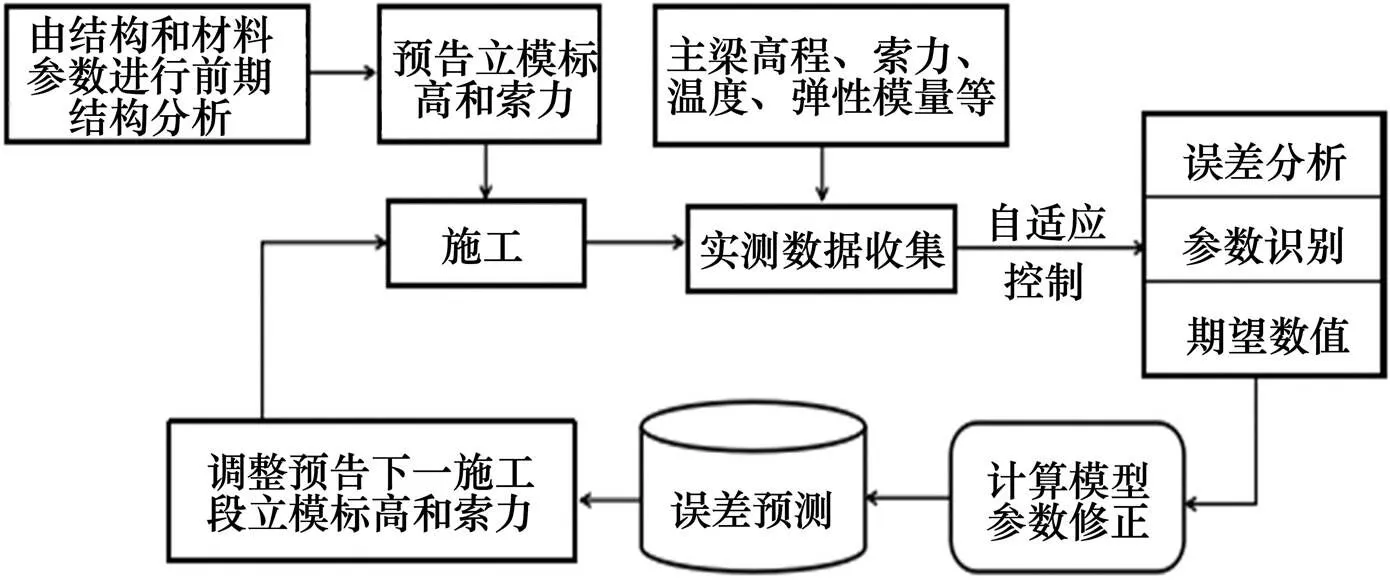
图1 线形控制原理模型框图

斜拉桥施工中立模标高的设定是线形控制的主要内容，直接决定了施工控制目的的实现。本文在自适应控制法的基础上对线形控制的偏差预测进行创新，对立模标高表达式引入修正值参数，通过收集的相关实测数据与理论数据的误差，直接对下一梁段立模标高修正值进行预测，进而对立模标高值进行调整预告，从而使实测主梁高程接近理论设计高程，成桥线形满足要求。式(1)为立模标高表达式。

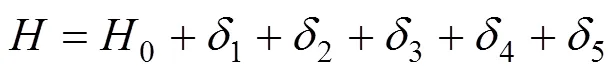
式中：0为主梁设计高程；1为设计成桥预抛高；2为施工预抛高；3为挂篮弹性变形值；4为温度影响调整值；5为修正值。修正值即是该梁段施工工序完成后，实测梁底高程与理论梁底高程的误差值。设计成桥预抛高和施工预抛高可以根据有限元分析模型仿真计算得出。挂篮弹性变形值也可以在施工过程中经过预压实验和实际测量变形值进行纠偏。温度修正值根据施工现场实测温度采用温度修正公式进行调整。实践证明5修正值相对较大，非线性明显，对悬浇段立模标高的误差有直接的影响，应对其进行重点控制。对于标准BP神经网络预测模型存在的问题，通过粒子群算法对BP神经网络的层间权值和节点阈值进行择优赋值，能够有效地规避局部最优解，提高逼近速度及预测准确性[8−13]。本文对立模标高的修正值将通过PSO-BP神经网络模型进行预测，从而对下一施工段的立模指令进行修正，达到线形优化的目的。

2 PSO-BP神经网络预测模型的实现方法

标准BP神经网络的学习是在层间随机赋予各传递路线权值及节点阈值，通过输入层的数据输入，由中间隐含层的转移函数和输出层的输出函数对求和后的传递数据进行运算输出，由前向后传递。当输出结果不满足期望条件，产生过大误差时，由后向前对各层的权值、阈值进行修正，不断往复地提高对输入模式的认识，使误差满足期望条件的学习过程。

神经网络学习过程中对输入层至隐含层的权值W、阈值θ(=1，2，…，；=1，2，…，)，中间层至输出层的权值V、阈值γ(=1，2，…，)进行初始化随机赋值，赋值区间为[−1,1]。

隐含层输出：

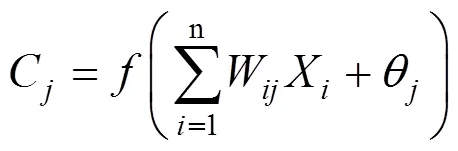
输出层输出：

众多的研究发现，对BP神经网络的层间权值和阈值进行随机赋值，是导致BP神经网络模型陷入局部极小值难以跳出的主要原因。为取得满意的预测效果，本文采用粒子群算法对标准BP神经网络的层间权值和节点阈值进行择优赋值。

粒子群算法(Particle Swarm Optimization，PSO)是一种群智能算法，具有算法结构简单，收敛速度快的优点，而且无须目标函数的梯度信息仅需要其输出值来对信息进行直接搜索。该算法将搜索空间中的每一个粒子(Particle)都看作是一个可能的解，并且所有的解都由目标函数的适应度值()来评价。每个粒子之间通过个体飞行经验和群体间的信息交流来改变自身的速度，调整飞行的方向和空间坐标，找到个体最优解()，进而以个体最优不断替换整体最优，得到群体最优解()。对于这2个最优解，粒子的迭代选择由下式定义。

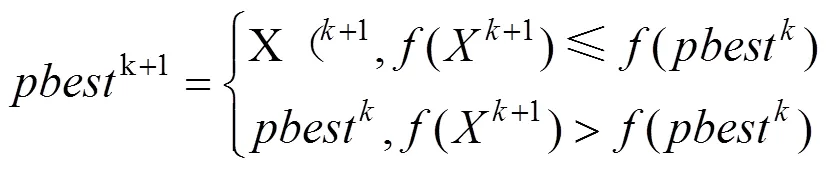
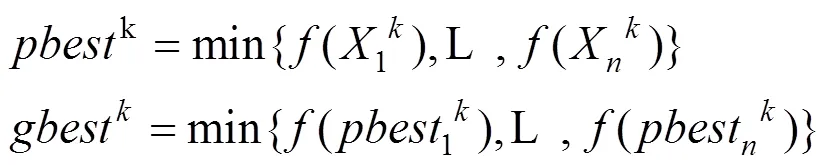
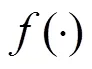
在粒子寻优中，每次逼近依照个体飞行经验和群体信息来更新粒子的速度和坐标，计算公式如式(6)所示。

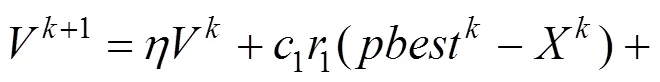
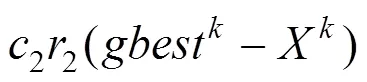
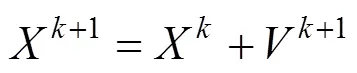
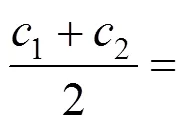
在平衡取值的关系上，大量的研究证实，对惯性权值采用线性递减的取值策略来改善优化算法的收敛性能相对简单，效果较好[15−16]。具体数学公式如下：

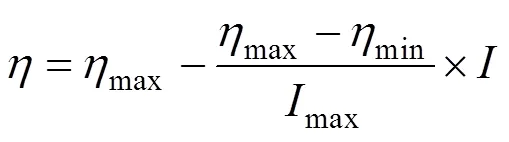
式中：max和min为惯性权值的最值；max为迭代最大次数；为当前迭代次数。

粒子的迭代更新过程由适应度函数来控制，把BP神经网络模型的预测值与期望值的均方差定义为粒子的适应度函数，即：

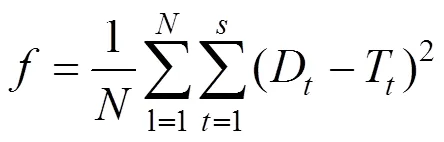
式中：为输出神经元个数；是预测输出值；是期望值，设有个训练样本。

在PSO-BP神经网络预测模型中，各输入输出参数及各层节点个数决定了粒子群算法的搜索维度，粒子的移动由适应度函数值来约束。根据迭代更新，粒子群体达到最高迭代次数或适应度函数值满足目标误差要求，则终止算法迭代并替换BP神经网络各层层间权值和节点阈值，最后对赋值更新后的网络模型进行仿真训练和预测输出。

3 工程实例及仿真结果分析

3.1 工程实例

河南省武陟至云台山高速公路跨南水北调主干渠特大桥为独塔单索面预应力混凝土斜拉桥，桥梁全长327.48 m，主桥跨径布置为175 m+93 m+49 m，共一联。桥梁采用不对称独塔单索面结构，塔梁墩固结，上部主梁采用标号C55现浇混凝土单箱三室箱梁。箱梁底宽13 m，顶宽27 m，中心梁高3.5 m，主跨标准索距为7 m。桥梁索塔承台以上高96 m。根据Midas/Civil桥梁有限元分析软件进行建模，共有节点310个，单元205个，并结合各施工工况对施工过程中的索力、预拱度、结构应力等参数进行了仿真计算分析。该斜拉桥仿真计算模型如图2所示。

图2 跨南水北调斜拉桥有限元模型

3.2 预测模型的参数选择

斜拉桥的预应力混凝土主梁悬臂施工控制影响因素复杂，精度误差不易实现。综合立模标高参数的影响因素，本文主要以主梁主跨的左幅为研究对象选取以下7个影响因素的数据作为输入层的输入参数，对网络模型进行训练。

1) 温度()。温度对主梁施工工况影响巨大。该工程在合龙前施工至主梁20号悬浇段时对全桥线形、索塔偏位、斜拉索索力等数据进行每3 h测量一次，不间断连续测量48 h的监测工作，测量结果显示，在日照温差(2016−07−03~2016−07−04)影响下：主梁线形最大高差为12 cm，索塔偏位最大偏差为3 cm，主跨索力变化最大的是S1#索，索力减少了213 kN，温度影响十分显著。本文选取主梁各悬浇段施工完毕体系转换后测量时的温度。

2) 施工梁段理论索力(F)及上一梁段的实测索力(F)。该理论索力是由设计单位提供的初拉索力。全桥合龙前主要以线形控制为主，而斜拉索为主要承重构件，索力大小对桥梁线形影响明显，应作为主要参考量。

3) 悬臂长度()。随着主梁的施工段不断推进，悬臂浇筑增大了对标高控制的难度。

4) 施工梁段梁底理论高程(H)及上一梁段的梁底实测高程(H)。临近施工段的实测梁底高程对误差修正值的影响显著。现场监控小组在悬臂段施工完毕后，于清晨温度变化小的时段进行高程测量工作。

5) 施工梁段的单根斜拉索钢丝重()。悬浇段的施工过程中使对应梁段斜拉索长度相应增加，而拉索在自重作用下垂度效应对整个结构的非线性影响不容忽视，应考虑其非线性因素影响。

该工程采用主跨(共22块)悬浇段的数据进行立模标高修正值的预测。其中1号现浇段距塔梁墩固结处较近，刚度较大，条件影响有限，故该段数据不做参考。数据输入从3号现浇段开始至15号段，共13组数据作为训练样本。由于斜拉桥施工工期跨度较大，较早施工完成段的数据对后续的施工段影响有限，故采用新陈代谢数列的训练样本逐段进行更新，即摒弃训练样本范围较早数据并且加入已完成梁段新测数据的方法对下一号段目标进行一步预测，进而完成对16号~22号共计7段的预测工作，从而使预测更符合现场施工实际。表1是部分训练样本数据。

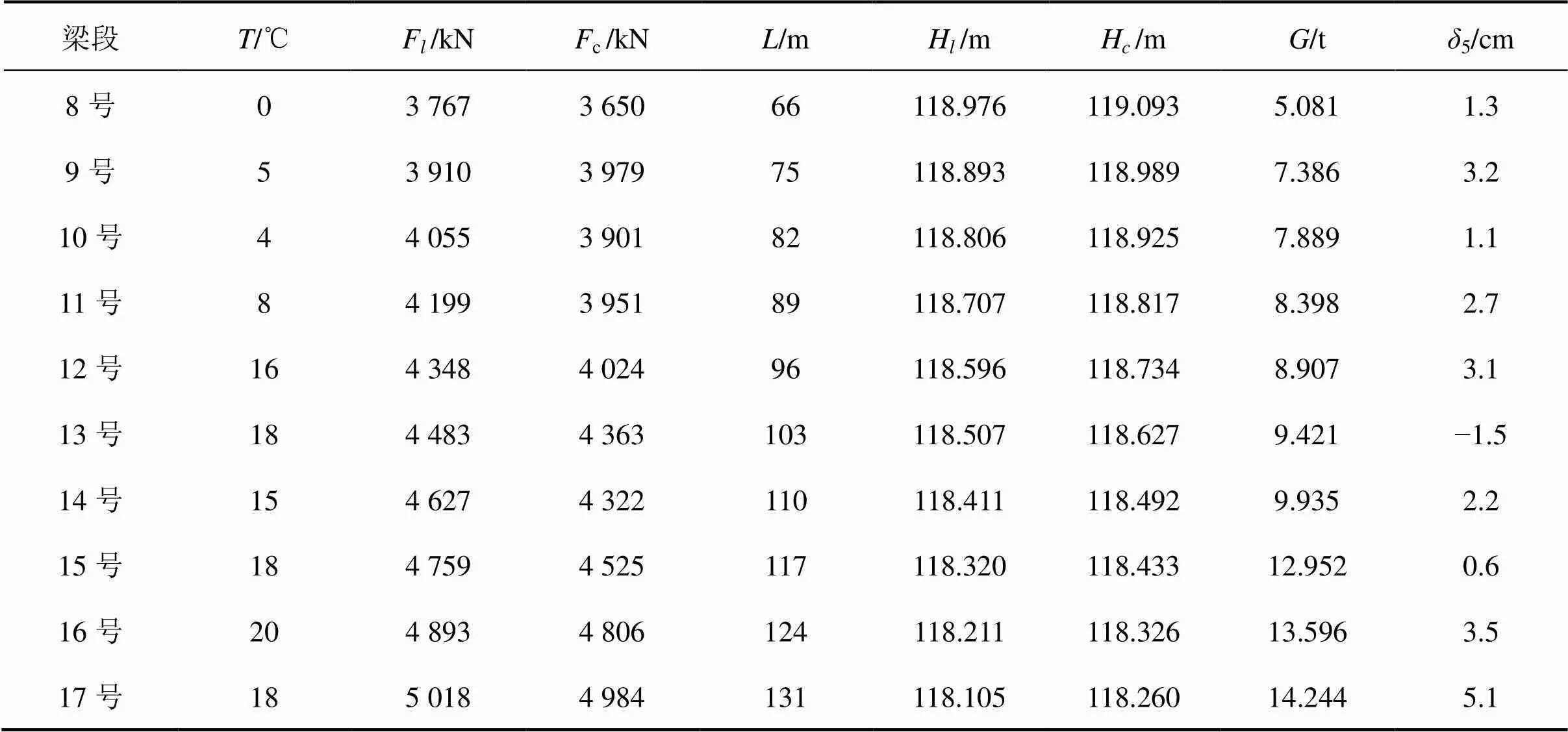
表1 主跨部分训练样本数据

3.3 预测效果验证

模型的建立通过网络结构的确定、粒子群算法寻优和BP神经网络预测来实现。由于工程实际情况的考虑仅选取了主跨13组样本进行训练，属于少样本的预测，故采用试凑法对BP神经网络中间层节点个数进行设置。通过MATLAB 2015 a建立7—20—1共3层BP神经网络预测模型，并编写程序以实现粒子群算法优化。选用表1中样本数据作为输入数据，粒子群搜索空间维度=7×20+ 20+20×1+1=181，种群规模为30，最大迭代次数为300，粒子最大移动速度max为1，目标误差精度为10−5，学习速率为0.1。

经过对数据样本的学习，预测模型表现出了较好的收敛效果，以对16号段的预测为例，粒子群算法中满足迭代要求，确定群体最优解后得到的最优适应度值为0.618 3，适应度值的降低正是各个粒子在目标函数下不断缩小搜索范围靠近全局最优解的过程，适应度值越小则说明寻优效果越好，得到的粒子个体较优越。粒子适应度值变化曲线如图3所示。

以最优粒子在空间中的位置信息对BP神经网络的层间权值及节点阈值进行更新，在BP神经网络模型中进行迭代计算，仅进行了4次迭代误差精度就达到了2.875 7×10−6，收敛速度快，满足10−5误差精度要求。图4为预测模型迭代图。

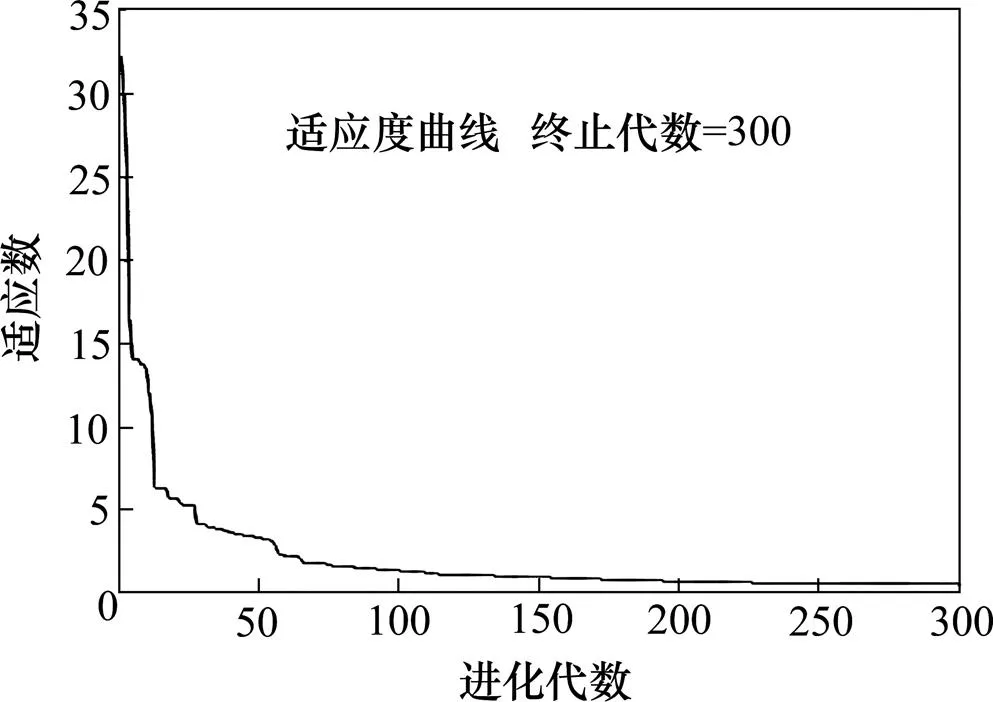
图3 适应度值变化曲线

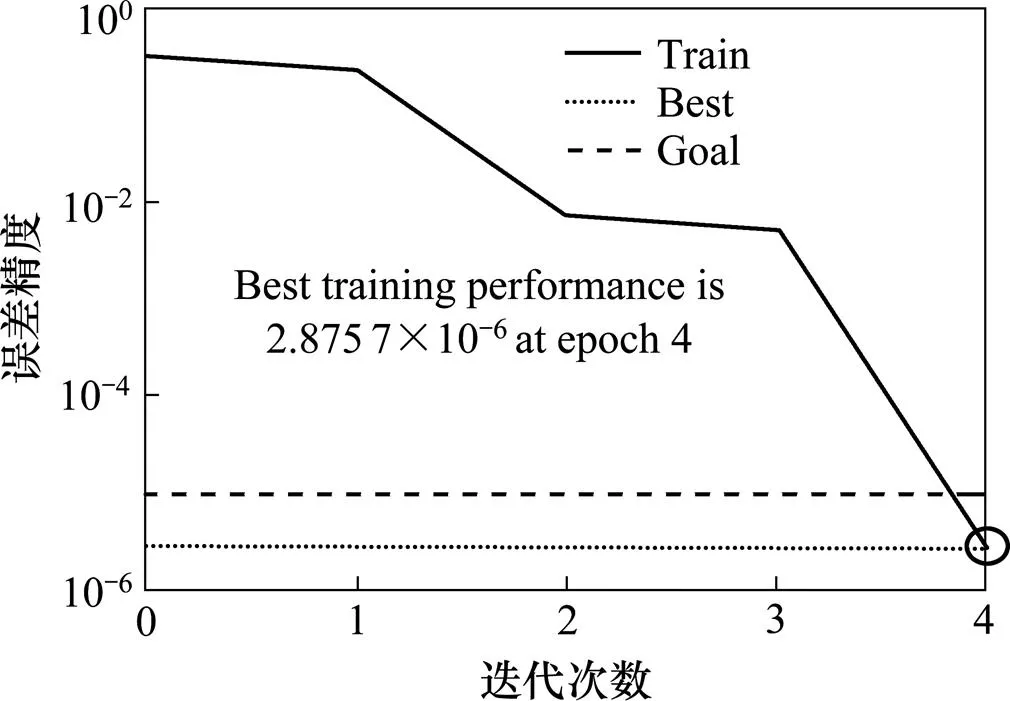
图4 PSO-BP神经网络预测模型迭代图

训练样本仿真输出值与目标实测值的误差如图5所示，可以看出数值误差非常小，网络的学习能力较强，预测结果具有可靠性。

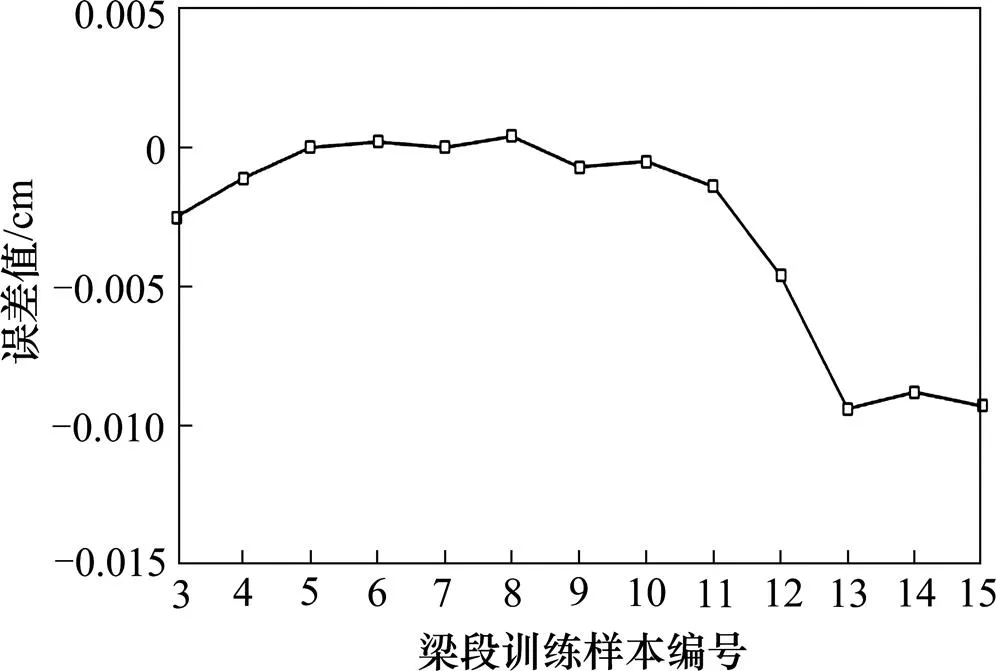
图5 训练样本预测值与实测值的误差

3.4 预测结果仿真分析

随着各梁段施工的完成，梁底实测标高与理论标高产生误差，并随着悬臂的伸长使控制难度加大，误差出现累积，会造成合龙困难。该桥的主跨悬浇段施工结束后的线形偏差如图6所示。

图6 主梁实测线形与理论线形对比图

本文分别采用了标准BP神经网络预测模型和PSO-BP神经网络预测模型对悬臂浇筑的16号~22号段的高程误差进行预测，表2为2种模型的预测结果，网络预测输出值与目标实测值对比如图7 所示。

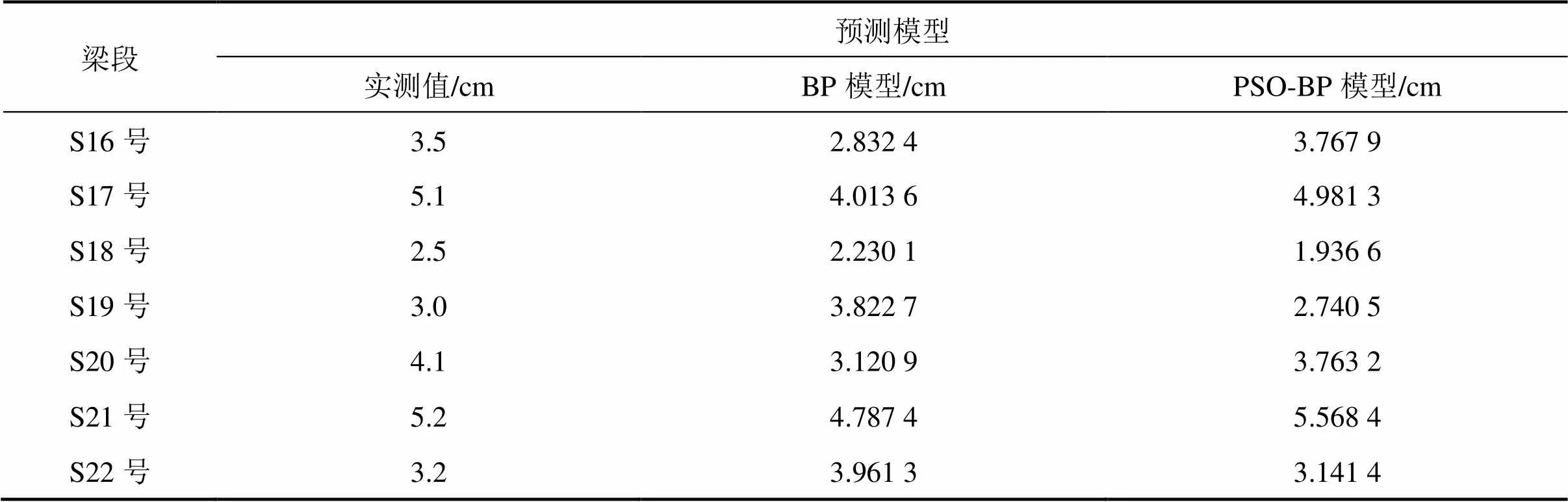
表2 修正值预测结果

图7 PSO-BP神经网络预测输出值与目标实测值对比图

表2给出了2种预测模型的预测结果，从实测值来看，目标数值相对较小，从而对模型预测精度提出了更高的要求。由PSO-BP预测模型得到的预测数据与实测值较为一致，其中最小相对误差在22号段只有1.8%，可见PSO算法对BP神经网络的优化效果显著，达到了较高的预测精度。图7中可以看出，BP神经网络模型预测结果与实测值有较大程度的偏差，最大相对误差在19号段达到了27.4%，整体预测精度偏低。虽然18号悬臂浇筑段预测结果稍逊于BP神经网络预测模型，但PSO-BP预测模型在整体上表现出了较好的稳定性，具有更加优秀的泛化能力。

因此在梁段施工前，采用PSO-BP预测模型的预测修正值数据对立模标高进行修正计算并指导施工，能够使梁段的标高更接近理论值，从而满足成桥线形的理论要求。对预测的修正值由Midas/ Civil有限元软件通过对梁段索力调整来实现并进行仿真分析，结果表明22号悬浇段施工完成后主跨4号控制截面应力测点下缘应力值为−3.53 MPa，与该处施工控制理论应力−3.6 MPa相吻合。22号段施工完成后主梁应力如图8所示，由此可知，经过设置优化后的立模高程值能够使主梁在满足成桥线形的同时，梁段受力也能达到较合理的施工状态，为主跨顺利合龙工作提供了有利条件。

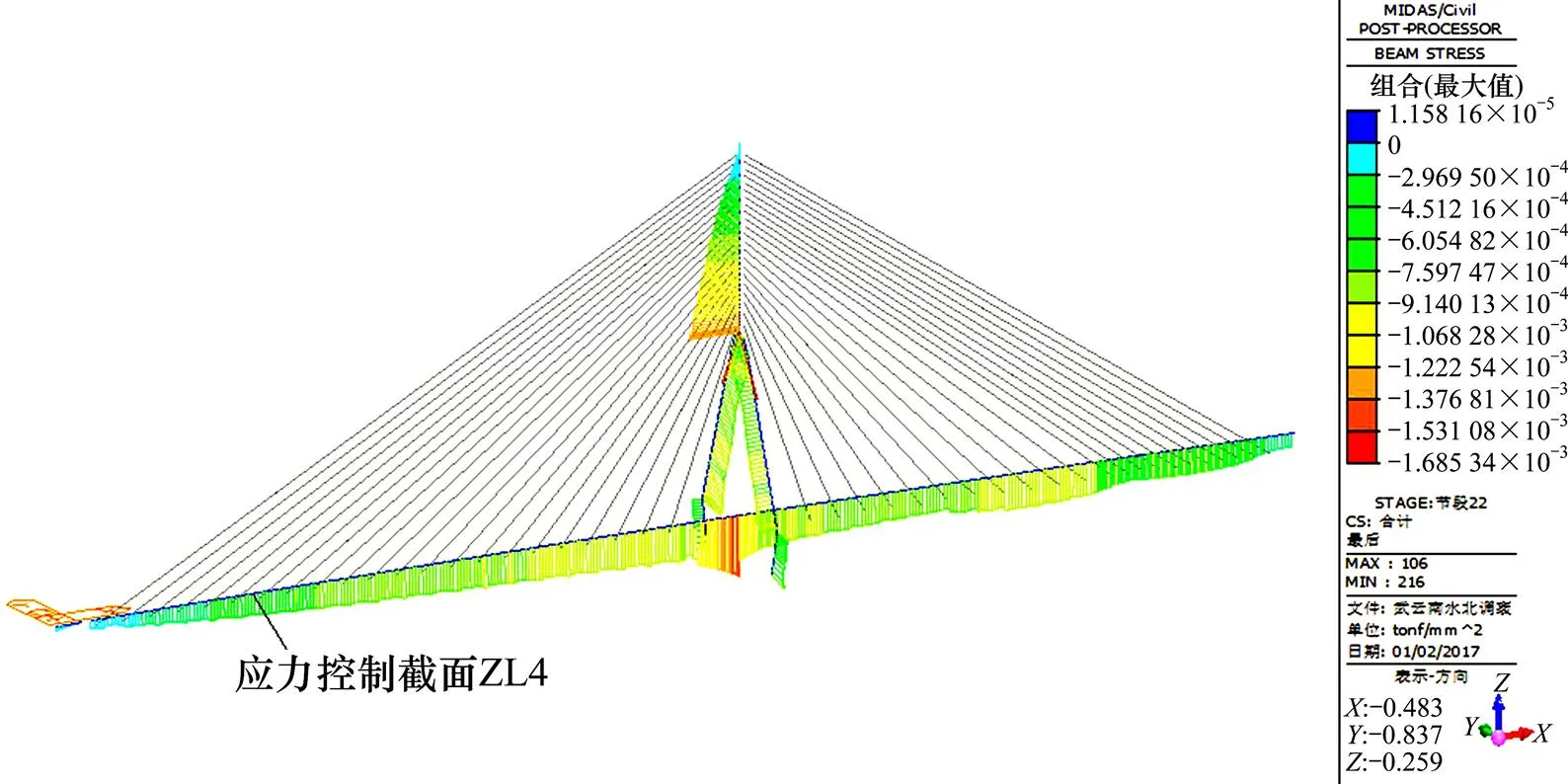
图8 22号段施工完成后主梁应力图

4 结论

1) 从预测结果来看，PSO-BP预测模型较标准BP神经网络预测模型具有更优的预测精度、逼近速度和稳定性，具有较好的预测泛化能力。

2) 该预测模型的实现能够指导主梁施工中立模标高的准确设定，使施工过程中主梁线形更接近理想成桥线形，主梁结构受力合理，有利于主梁合龙施工及成桥状态的实现。

3) 本文提出的线形预测模型可为斜拉桥主梁线形优化提供参考，同时该模型也可以对索力误差预测进行尝试和探索。此外也为桥梁施工控制工作提供了新的思路和方法。

[1] 刘建威, 钟泽湘. 基于改进灰色GM(1,1)模型的高速公路路基沉降预测[J]. 铁道科学与工程学报, 2015, 12(6): 1369−1373.

LIU Jianwei, ZHONG Zexiang. Prediction of expressway subgrade settlement based on animproved gray prediction model[J]. Journal of Railway Science and Engineering, 2015, 12(6): 1369−1373.

[2] 崔雍, 楚小刚, 董嘉, 等. 基于神经网络的桩基竖向承载力预测研究[J]. 铁道工程学报, 2016, 33(4): 65−69.

CUI Yong, CHU Xiaogang, DONG Jia, et al. Prediction research on the vertical bearing capacity of pile foundation based on neural network[J]. Journal of Railway Engineering Society, 2016, 33(4): 65−69.

[3] 陈治亚, 周艾飞, 谭钦之, 等. 基于改进的BP人工神经网络的物流需求规模预测[J]. 铁道科学与工程学报, 2008, 5(6): 62−68.

CHEN Zhiya, ZHOU Aifei, TAN Qinzhi, et al. Forecasting model for the scale of logistics demand based on the improved back propagation artificial neural network[J]. Journal of Railway Science and Engineering, 2008, 5(6): 62−68.

[4] 林元培. 卡尔曼滤波法在斜拉桥施工中的应用[J]. 土木工程学报, 1983, 16(3): 7−14.

LIN Yuanpei. Application of Kalman’s filtering method to cable-stayed bridge construction[J]. China Civil Engineering Journal, 1983, 16(3): 7−14.

[5] 陈建阳, 向木生, 郭峰祥, 等. 大跨度桥梁施工控制中的神经网络方法[J]. 桥梁建设, 2001(6): 42−45.

CHEN Jianyang, XIANG Musheng, GUO Fengxiang, et al. Neural network method in construction control for long-span bridge[J]. Bridge Construction, 2001(6): 42− 45.

[6] 禚一, 王菲. 基于人工神经网络的混合梁斜拉桥智能诊断方法研究[J]. 铁道工程学报, 2011, 28(12): 57−63.

ZHUO Yi, WANG Fei. Research on intelligent diagnosis methods of a hybrid girder cable-stayed bridge based on artificial neural networks[J]. Journal of Railway Engineering Society, 2011, 28(12): 57−63.

[7] GUO Z, ZHAO W, LU H, et al. Multi-step forecasting for wind speed using a modified EMD-based artificial neural network model[J]. Renewable Energy, 2012(37): 241−249.

[8] SHA F, ZHU F, GUO S N, et al. Based on the EMD and PSO-BP neural network of short-term load forecasting[J]. Advanced Materials Research, 2013(614): 1872−1875.

[9] 陈啸, 王红英, 孔丹丹, 等. 基于粒子群参数优化和BP神经网络的颗粒饲料质量预测模型[J]. 农业工程学报, 2016(14): 306−312.

CHEN Xiao, WANG Hongying, KONG Dandan, et al. Quality prediction model of pellet feed basing on BP network using PSO parameters optimization method[J]. Transactions of the Chinese Society of Agricultural Engineering, 2016(14): 306−312.

[10] 高峰, 冯民权, 滕素芬. 基于PSO优化BP神经网络的水质预测研究[J]. 安全与环境学报, 2015, 15(4): 338− 341.

GAO Feng, FENG Minquan, TENG Sufen. On the way for forecasting the water quality by BP neural network based on the PSO[J]. Journal of Safety and Environment, 2015, 15(4): 338−341.

[11] 魏津瑜, 张玮, 李欣. 基于PSO-BP神经网络的高炉煤气柜位预测模型及应用[J]. 中南大学学报, 2013, 44(1): 266−270.

WEI Jinyu, ZHANG Wei, LI Xin. BFG forecasting model and application based on PSO-BP neural network model[J]. Journal of Central South University (Science and Technology), 2013, 44(1): 266−270.

[12] 李文生, 姚琼, 邓春健. 粒子群优化神经网络在动态手势识别中的应用[J]. 计算机工程与科学, 2011, 33(5): 74−79.

LI Wensheng, YAO Qiong, DENG Chunjian. Application of the BP neural network based on PSO in dynamic gesture recognition[J]. Computer Engineering & Science, 2011, 33(5): 74−79.

[13] 于涛.BP神经网络在大型斜拉桥施工控制中应用研究[D]. 南京: 河海大学, 2007.

YU Tao. The application of BP neural network on cable-stayed bridge’s construction control[D]. Nanjing: Hehai University, 2007.

[14] Clerc M, Kennedy J. The particle swarm-explosion, stability, and convergence in a multi-dimensional complex space[J]. IEEE Transactions on Evolutionary Computation, 2002(1): 58−73.

[15] Shi Y, Eberhart R C. Empirical study of particle swarm optimization[C]// Proceedings of IEEE Congress on Evolutionary Computation (CEC), Piscataway, NJ, USA, 1999: 1945−1950.

[16] 陈贵敏, 贾建援, 韩琪. 粒子群优化算法的惯性权值递减策略研究[J]. 西安交通大学学报, 2006, 40(1): 53−56.

CHEN Guimin, JIA Jianyuan, HAN Qi. Study on the strategy of decreasing inertia weight in particle swarm optimization algorithm[J]. Journal of Xi’an Jiaotong University, 2006, 40(1): 53−56.

Study on predication of line optimization of large-span concrete cable-stayed bridges

YU Jingfei1, WU Yankui1, SU Xing2

(1. School of Civil Engineering, Inner Mongolia University of Science and Technology, Baotou 014010, China; 2. Henan Province Highway Engineering Bureau Group Co., Ltd, Zhengzhou 450009, China)

The large-span concrete cable-stayed bridge has rather complex construction procedure. It is affected by non-linear factors such as cable sag, temperature variation as well as shrinkage and creep of concrete etc in the construction process, which then leads to relatively large error of setting of formwork erection elevation. In this case, the ideal completed bridge state can hardly be achieved. In order to guarantee accurate bridge line and balanced structure stress, factors influencing the formwork placing elevation of construction are analyzed comprehensively. A predictive model of the modified value of formwork placing elevation based on the PSO-BP neural network is established, so as to predict the modified value of the formwork placing elevation. The simulation results indicated that the established model with stable performance has very good predication and generalization abilities. Lines obtained from forecasted results were closer to ideal completed bridge lines. The main girder structure with reasonable stress achieved favorable completed bridge state, which also provides certain reference for line optimization methods of cable-stayed bridges.

formwork placing elevation; cable-stayed bridge construction; particle swarm optimization; neural network; line optimization

U445

A

1672 − 7029(2018)01 − 0133 − 08

2016−12−19

内蒙古自治区自然科学基金资助项目(2016MS0723)

于景飞(1974−)，男，内蒙古赤峰人，副教授，从事桥梁施工监控研究；E−mail：yujf@imust.edu.cn