装配式梁桥整体托换装置及瞬态冲击效应研究
黄海新,李晓迪,程寿山,韩立中
(1.河北工业大学 土木与交通学院,天津 300401;2.交通运输部公路科学研究所,北京 100080)
0 引言
近年来我国桥梁建设成绩斐然,其中装配式混凝土梁桥在中小跨径结构中占比很大.但由于承载能力提升、年久失修结构劣化严重等原因,部分结构需拆除更换[1].传统的拆除方法是采用大型吊车、浮吊等进行单片切割吊拆后单片安装[2],但该方法对桥梁下部净空要求较高,尤其对桥下有通航、通行要求的结构更是存在干扰大、风险高,难以实施的问题.
针对上述问题,本文以一跨线装配式混凝土梁桥为工程背景,提出了一种施工简便快捷、安全性高,对交通运营几乎无干扰的整体托换装置,同时就该装置平移瞬间的冲击效应进行了研究,所得结论对工程实践具有一定的指导意义.
1 工程概况及改造方案
某装配式混凝土梁桥,桥梁上部结构为1×13 m钢筋混凝土T梁,横向布置6片,梁高1.3 m,设6道横隔板(见图1).该桥经检测评定为五类桥,需拆除重建.
由于该桥跨客运专线,梁底距高压线很近,传统单片拆除单片安装的方式难以适用.为此,在吸收借鉴桥梁中顶推法[3]和建筑中整体平移技术[4]的基础上,提出了一种整体托换改造装置,如图2所示.
托换改造装置设在待拆梁体上部,由钢构件拼装而成.主要包括设置在桥台两侧支撑在现浇混凝土横梁上的钢立柱、柱顶部工字钢端横梁、纵梁和移动横梁.其中,纵梁上设置副滑道,移动横梁在其上滑动,横梁通过柔性吊杆与设于待拆梁体一端的底部兜底横梁相连,混凝土梁体的另一段采用刚性滑动支承,并将在设于桥跨外侧的主滑道上滑动.既有装配式混凝土梁体拆除过程为先进行竖向顶升,既而利用卷扬机拖曳梁体将其整体移出既有线路后破拆.新梁更换安装时工艺流程与拆除相反,即采用先在桥跨外侧整体组拼,而后整体平移到桥位处落梁.
主副滑道和刚柔两种支撑方式的设置,不同于一般的整体平移装置,这也导致了在整个平移过程中,下部主梁整体在卷扬机的牵引下先匀速移动,至吊杆倾斜至一定角度后移动横梁才能开始移动,而由于静动摩擦的瞬态切换势必导致移动横梁对结构产生冲击效应,这对结构带来的影响究竟有多大,其变化规律如何值得进一步探讨.

图1 桥梁工程图Fig.1 Photo of bridge
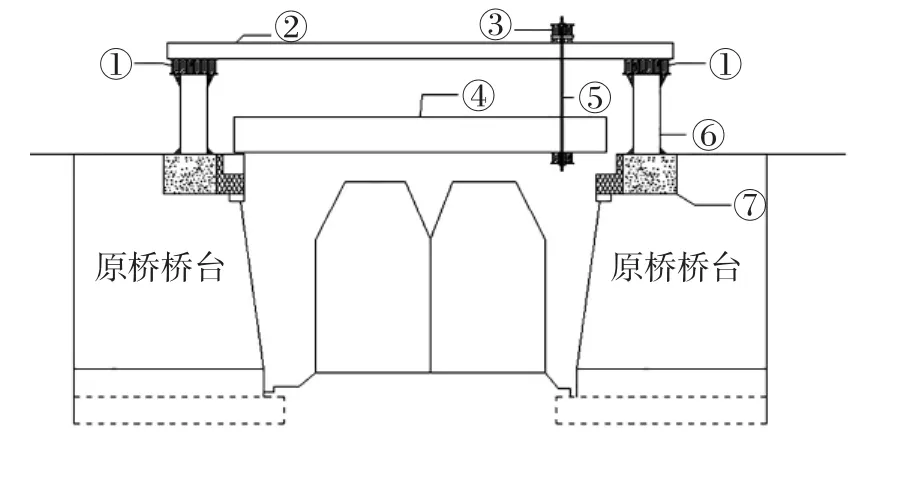
图2 桥梁改造立面图Fig.2 Elevation of bridge rehabilitation
2 理论分析
2.1 动力学方程的建立
以装置中移动横梁为研究对象,其简化的力学计算模型如图3所示.
设上部移动横梁开始运动作为t=0时刻,根据达朗伯原理,可得移动横梁受力应满足如下平衡方程式
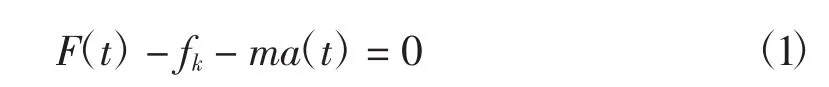
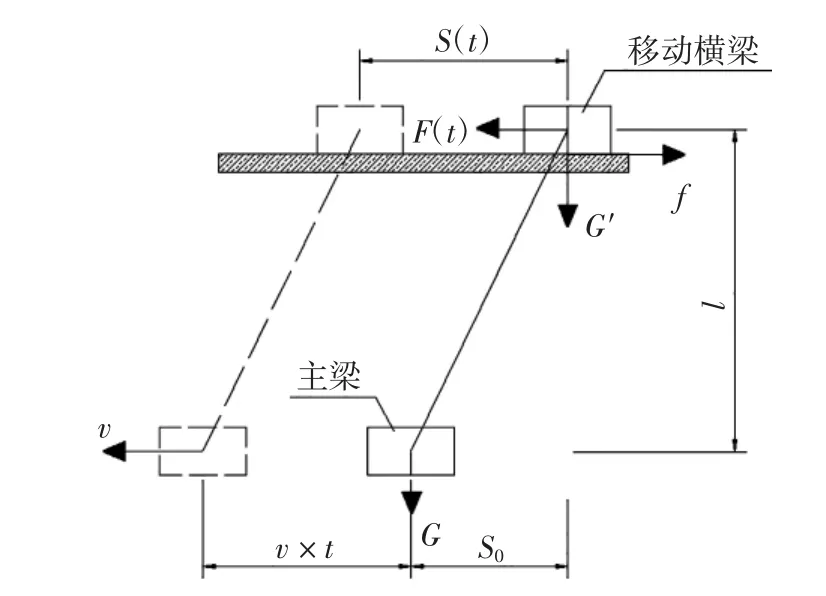
图3 移动横梁力学计算模型Fig.3 Mechanical model of moving crossbeam
横梁即将移动时刻力矩平衡,可得方程

在移动横梁即将移动时,应有

式中:F(t)为移动横梁所受的水平分力,N;fk为移动横梁所受的滑动摩擦力,N;m为移动横梁的质量,kg;a(t)为移动横梁移动过程中的加速度,m/s2;G′为移动横梁所受的竖向分力,N,由图2中结构布局知,其为下部混凝土主梁自重的一半;S0为移动横梁即将移动时与下部混凝土主梁的位移差值,m;S(t)为移动横梁的位移,m;v为混凝土主梁平移速度,m/s;t为移动横梁运动的时间,s;fs为移动横梁所受的最大静摩擦力,N;l为移动横梁与混凝土主梁竖向垂直距离,m.
需要说明的是,这里摩擦力按照正压力与摩擦系数的乘积计算,且假定摩擦系数为常量,即
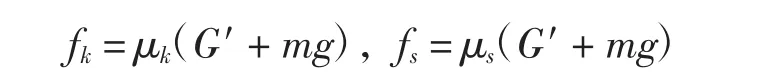
其中,μk和μs分别为动、静摩擦系数.
联立式 (1) 和式(2),可得
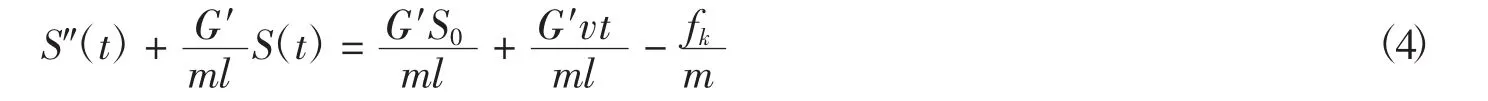
将式(3) 代入式(4),得微分方程通解为

在t=0时,有初始条件S(0)=0,S′(0)=0,代入式(5)可得

将改造工程中相关数据代入上式,可得移动横梁位移表达式

由式(6)可知,移动横梁位移与移动横梁静动摩擦系数的差值、下部混凝土梁体移动速度v有关.
2.2 梁体运动协调性分析
基于上述方程(6)可以获得移动横梁自身的位移时程曲线,但对工程而言,技术人员可能更关心移动初期,由于静动摩擦的瞬态切换对改造装置及混凝土梁体本身带来的冲击效应,以及上部移动横梁移动后和下部混凝土梁体间的相对位置关系,因为这直接涉及到上下部梁体运动的协调性,而这会对结构产生不同程度的影响.
为此,这里着重分析静动摩擦系数的不同比值对上下部梁体运动协调性的影响,希望找到移动横梁追上下部混凝土主梁的临界点.
假定下部混凝土主梁以速度v匀速运动,由于移动横梁初始时刻存在位移差S0,因此当vt+S0≤S(t)时,移动横梁才能追上混凝土主梁.结合式(5),得移动横梁与下部混凝土主梁位移差值表达式为


移动横梁若能追上下部混凝土梁体,应有△S(t)≤0.由式(8)解得

可见,当动静摩擦系数的比值等于0.5时,后期移动的移动横梁即可追上下部先移动的混凝土主梁,由此可获得二者运动位置的临界状态△Smin=0.
将改造工程中相关数据代入,上下部梁体位移差值可表示为
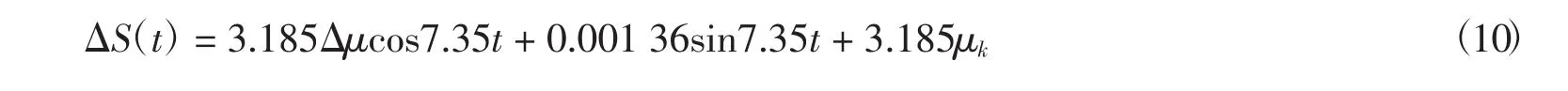
3 数值模拟
数值模拟的目的,一方面检验前面建立的移动横梁运动方程的正确性,同时可更为直观地全程展示移动横梁及其与下部梁体间位置关系及受静动摩擦系数的影响,尤其便于体现理论表达式未计入的瞬态冲击效应的强烈程度.
3.1 模型建立
利用Abaqus软件对梁体平移过程进行模拟.限于电脑内存并为缩短运营时间,根据分析重点,将模型加以简化,即将混凝土梁体简化为一长方体质量块,上部纵梁固定,忽略钢立柱及端横梁,纵梁和顶部移动横梁间设置为滑动接触,动、静摩擦系数均假定为常量.移动横梁通过两根吊杆与下部梁体相连,模型如图4所示.
3.2 仿真分析
3.2.1 模型检验
图5给出了在静摩擦系数μs=0.06的情况下的移动横梁上吊点处节点理论计算和数值模拟结果位移对比情况.
从图5可见,理论和数值计算结果吻合较好,验证理论模型正确性的同时,亦表明有限元数值模型的精度,混凝土梁体的平移过程可通过该模型仿真模拟.
3.2.2 工况选取及模拟结果
根据前面的理论推导,在设定下部混凝土主梁平移速度为0.01 m/s的前提下,按照移动横梁能否追上下部梁体的情况,选取3种不同的动、静摩擦系数组合工况进行分析.其中,动摩擦系数μk根据相关资料[8]选取0.03,静摩擦系数μk则分别取:工况①0.05;工况②0.06;工况③0.11.
图6~图8分别给出了3种静动摩擦系数工况下移动横梁和下部梁体的位移时程变化.此外,为量化体现冲击效应的强烈程度,这里同时给出了混凝土主梁吊点处应力变化曲线.

图4 简化有限元模型Fig.4 Simplified finite element model
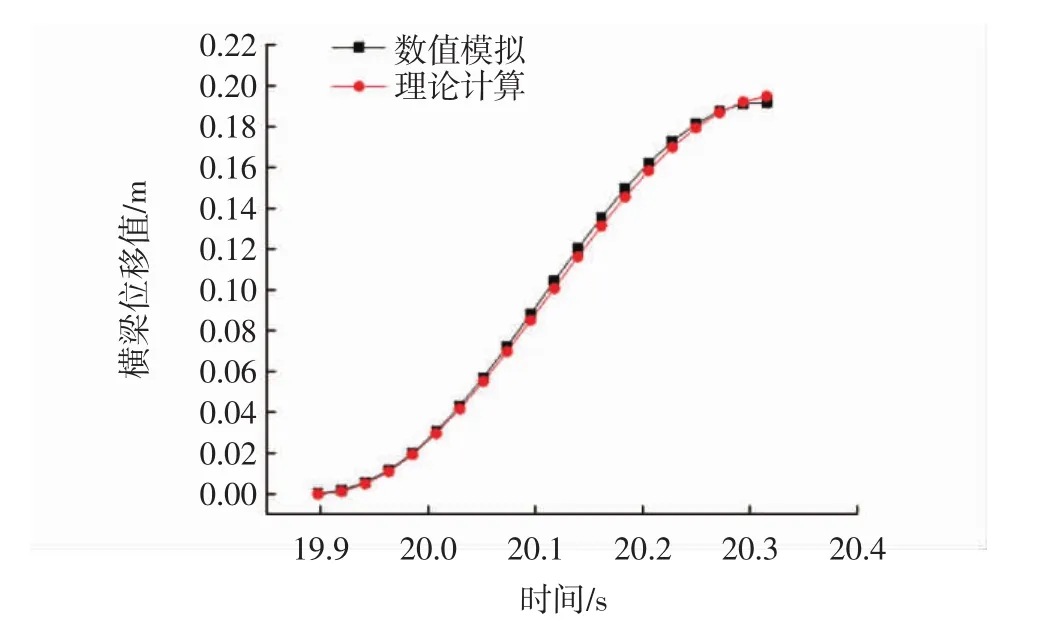
图5 移动横梁吊点处节点理论和数值结果位移对比图(μs=0.06)Fig.5 Theoretical and numerical displacement of moving crossbeam(μs=0.06)

图7 移动横梁位移、主梁位移及其吊点处主应力(μs=0.06)Fig.7 Displacement of moving crossbeam and mainbeam as well as stress of mainbeam suspension element(μs=0.06)
3.2.3 结果分析
就主梁平移过程中上下部梁体的位移时程而言,从图6~图8可以看出,主梁位移一直均匀增加,而移动横梁则出现从移动到静止,再从静止到移动的周期性变化,具体为先为下部主梁整体匀速移动,结合图3知移动横梁至吊杆倾斜至一定角度后才开始移动,且移动迅速,有时甚至超过下部主梁右端,之后静止,等到第2次拉起再移动,往复进行.其原因在于,初期主梁移动吊杆倾角较小,此时拉力小于最大静摩擦力,移动横梁不会同步移动,在吊杆倾斜至一定角度后,吊杆拉力随之增大到最大静摩擦力,移动横梁开始移动.移动瞬间由于动、静摩擦系数的切换,摩擦力减小至滑动摩擦力,而吊杆拉力此时由于滞后性仍为最大静摩擦力,移动横梁迅速向前加速移动,吊杆倾斜角度逐渐变小,直到吊杆拉力减小到动摩擦力,此时移动横梁由于惯性继续向前减速移动,Δμ较大时甚至超过下部梁体右端,之后随着动能下降而静止.而后,照此周期性运动.图6中工况①表明,μs取0.05时,移动横梁整个平移过程中一直滞后于下部混凝土主梁;图7中μs取0.06时,上下部梁体某个时刻可正好处于相遇的临界状态;图8中μs取0.11时,则出现了上部移动横梁可追上并超越主梁的现象,这些现象与理论推导的结论均一致.
在不同μs情况下,对比移动横梁位移图可知,μk保持不变,μs越大,移动横梁初始移动时间越晚,其原因可由前面理论推导解释,根据理论分析,两梁体初始位移差为S0=3.185μs,随着μs的增大,S0逐渐增大,即吊杆倾角越大,3种工况下主梁移动速度不变,故有移动横梁初始移动时间必然随着μs的增大而推迟.
为清晰体现移动横梁的静动摩擦瞬态切换对结构带来的冲击效应,这里将移动横梁移动瞬间对应的主梁吊点处主应力(遵循von Mises应力准则)时程曲线加以局部放大,如图9~图11所示.

图8 移动横梁位移、主梁位移及其吊点处单位主应力(μs=0.11)Fig.8 Displacement of moving crossbeam and mainbeam as well as stress of mainbeam suspension element(μs=0.11)
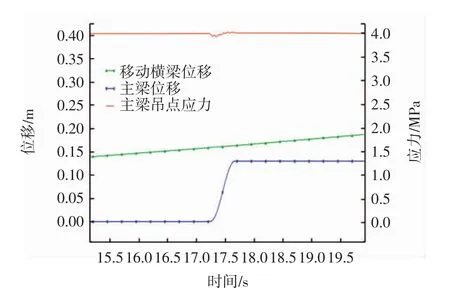
图9 移动横梁位移、主梁位移及其吊点处主应力局部放大图(μs=0.05)Fig.9 Local displacement of moving crossbeam and mainbeam as well as stress of mainbeam suspension element(μs=0.05)
从图中可见,3种工况下移动横梁移动的瞬间主梁吊点处的应力均呈现先突然减小而后增加的变化.分析该现象,应该是由于移动横梁在动静摩擦力切换瞬间突然移动,导致下部梁体产生向下的加速度,吊杆拉力突减所致,这一点可从影响主梁吊点应力的主要分量σy的突然下降可知(见图12).而当移动横梁静止后,吊杆拉力逐渐恢复,下部梁体吊点处应力增大.
对比3种工况模拟结果,可知虽然主梁吊点处应力变化总趋势相同,但在移动横梁开始运动到静止的一个周期内,主梁最大值出现的时刻及应力波动变化的程度不同.工况①中移动横梁未追上主梁,应力最大值出现在移动横梁即将静止前两梁体水平位移差最小的时刻;工况②中移动横梁恰好在静止时追上主梁,应力最大值出现在移动横梁静止的时刻;工况③中移动横梁追上并超越主梁,应力最大值出现在移动横梁刚好追上主梁的时刻.总体来说,3组主梁应力最大值均出现在两梁体水平位移差最小的时刻.
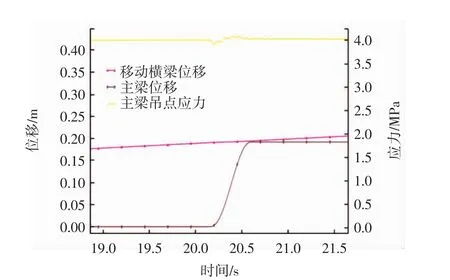
图10 移动横梁位移、主梁位移及其吊点处主应力局部放大图(μs=0.06)Fig.10 Local displacement of moving crossbeam and mainbeam as well as stress of mainbeam suspension element(μs=0.06)
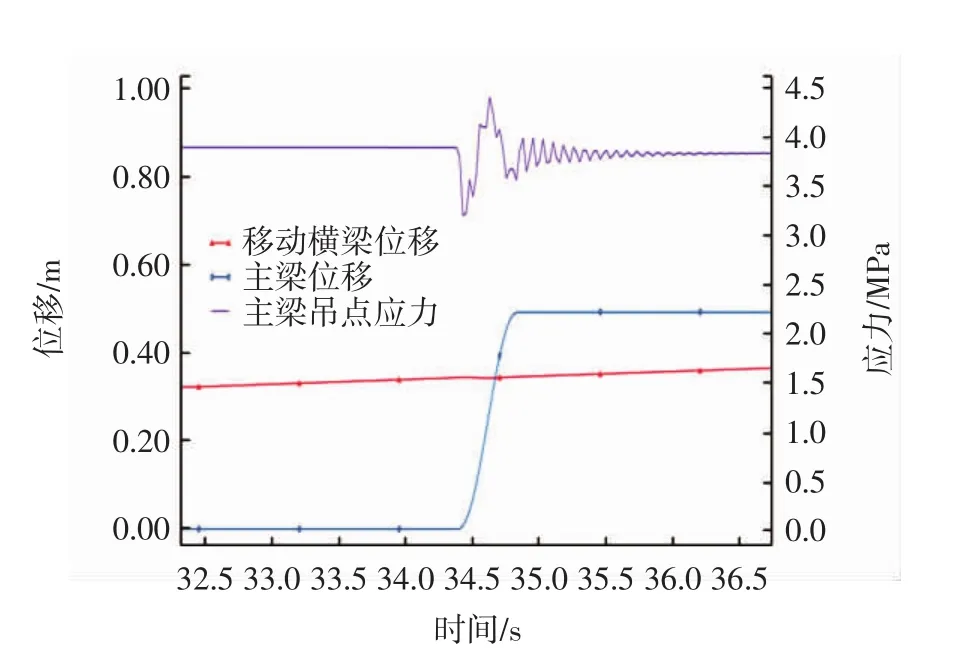
图11 移动横梁位移、主梁位移及其吊点处主应力局部放大图(μs=0.11)Fig.11 Local displacement of moving crossbeam and mainbeam as well as stress of mainbeam suspension element(μs=0.11)
表1中给出了3种工况下混凝土主梁吊点处应力数值.可见,工况①中主梁一个周期内应力最大变化幅度为2.5%;工况②中主梁一个周期内应力最大变化幅度为4.7%;工况③中主梁一个周期内应力最大变化幅度为37.3%.前2个工况应力波动变化幅度较小,对结构冲击效应不明显,而工况③应力变化幅度显著,对结构带来了一定程度的冲击效应,不过好在仍小于混凝土梁体的容许应力,可以确保主梁平稳出入桥位.
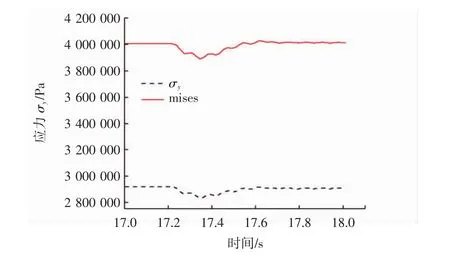
图12 主梁吊点单元应力与竖向分应力σy图Fig.12 Stress of mainbeam suspension element as well as vertical stress(μs=0.05)

表1 主梁吊点处单元应力MPaTab.1 Stress of mainbeam element at suspension node
4 结论
1) 针对桥下改造空间受限的装配式混凝土梁桥,传统的单片切割拆除单片安装的改造技术难以适用的状况,给出了一种刚柔支撑的整体托换装置,该装置由常规钢构件组拼而成,上下部设置主副滑道,在卷扬机的牵引下移动,具有施工简便,无需大型起吊机具、造价低、工期短、对周边环境影响小的特点.
2)基于达朗伯原理,建立了移动横梁动力学方程,该方程能考虑静动摩擦系数的影响,并能体现主梁平移过程中与上部移动横梁间的位置关系,理论推得动静摩擦系数比值0.5是移动横梁能否追上下部梁体的临界点.
3)选取混凝土梁体吊点处的应力,研究静动摩擦切换瞬间的冲击效应.结果表明,移动横梁移动瞬间主梁吊点处应力突然减小,而后梁体吊点处应力最大值出现在移动横梁与主梁水平位移最小的时刻.
[1] 桂学.桥梁顶升技术研究[D].西安:长安大学,2005.
[2] 杨显维,杨文强.混凝土梁式桥拆除技术分析[J].天津建设科技,2013,23(5):57-59.
[3] 宋延旭.顶推施工阶段钢箱梁桥受力性能研究[D].北京:北京交通大学,2010.
[4] 袁放.既有线上跨桥梁同步顶升与平移技术研究[D].上海:华东交通大学,2010.
[5] 程海根.邹常进.同步顶升解决跨线桥净空问题关键技术探讨[C]//第十八届全国桥梁学术会议,2008.
[6] 臧小萌.浅谈七里河黄河大桥主桥上部结构拆除方法[J].甘肃科技,2011,23(24):129-130.
[7] 石亦平,周玉蓉.ABAQUS有限元分析实例详解[M].北京:机械工业出版社,2006.
[8] 张俊义.桥梁施工常用数据手册[M].北京:人民交通出版社,2005.
[9] 陈松,卓静,朱雪源.一种小跨径桥梁快速改造新技术[J].公路工程,2016,41(1):81-84.
[10]姚玲森.桥梁工程[M].北京:人民交通出版社,2012.
[11]蒋岩峰.移位技术在桥梁改造中的应用[J].中国公路,2011(13):86-89.
[12]李小军.64 m系杆拱梁横移施工技术[J].中国公路,2011(7):180-181.
[13]Beaney N J,Martin J M.Design and construction of Dornoch Firth Bridge[C]//Construction Proceedings of Institution Civil Engineering.Transportation,Aug 1993.
[14]黄侨,赵银飞,孙永明.大跨度提篮式人行拱桥的振动病害分析与改造[J].公路交通科技,2008,25(10):88-92.
[15]卫星,强士中,高伟.旧桥加固中的一种常用方法[J].公路交通科技,2002,19(5):85-87.
[16]封建武.高速公路上跨桥整体顶升技术[J].城市道桥与防洪,2008,2(2):52-55.
[17]刘富勤.整体平移技术在城区改造中的应用研究[D].武汉:武汉理工大学,2005.
[18]李爱群,吴二军.我国建筑物整体平移技术及工程应用进展[J].江苏建筑,2003(S):48-54.

