BM理论优化计算在Ti-49.8Ni合金Ⅱ型孪晶马氏体相变中的应用
孙 颖,苏 慧,许长庆
(河北工业大学 材料科学与工程学院,天津 300130)
0 引言
表象理论包括Wechsler、Read[1-2]等提出的WLR理论以及由Bowles和Mackenzie[3-4]提出的BM理论.表象理论是基于马氏体和母相的点阵参数以及马氏体和母相的点阵对应关系,从而计算出惯习面等晶体学参数的理论,成功解释了孪晶马氏体的相变晶体学,包括新相和母相间的位向关系、惯习面和表面浮凸等晶体学特征,为研究合金的宏观性能提供理论依据.本文对经典BM理论中直线不变应变L的求解方法进行改进[5-6],并利用此理论对Ti-49.8Ni合金马氏体相变进行晶体学计算.
1 Ti-49.8Ni晶体结构和相变晶体学
Ti-49.8Ni合金马氏体体相变是B2-B19′相变,其中母相为B2结构,点阵参数a0=0.301 5 nm;马氏体相为B19′单斜结构,点阵参数为a=0.288 9 nm,b=0.412 0 nm,c=0.462 2 nm,β=96.8°[7].
对于Ti-49.8Ni合金中〈011>MⅡ型孪晶马氏体相变有关学者做出了相关计算.1981年,Knowles和Smith[8]通过透射电镜分析观察到的〈011>MⅡ型孪晶的孪生面与(344)M相差8.86°,由(011)M主平面和(111)M台阶面组成,由此得到孪晶面为并通过WLR理论计算推论〈011>MⅡ型孪晶可作为TiNi合金马氏体相变的点阵不变切变;Matsumoto等[9]获得了关于Ti-49.8Ni合金比较完整的实验数据和晶体学数据,并发现只有型孪晶得到的晶体学参数与实验值符合.
2 Bain应变
Ti-49.8Ni合金的马氏体相变是由立方结构(B2)转变为单斜结构(B19′),晶体学上可看作由体心点阵中得到一个四方晶胞,如图1a)所示;再由四方晶胞(实线)转变为单斜晶胞(虚线),如图1b)所示.其中,(i,j,k)为立方系的主坐标轴,(i′,j′,k′)为四方晶胞的主坐标轴.

图1 立方 (B2) 转变为单斜 (B19′) 晶胞Fig.1 Cube (B2) into monoclinic (B19′) cell
根据图1得到马氏体和母相的点阵对应关系为

关于 i′,j′和 k′的 Bain 应变矩阵为

母相坐标系统中发生的Bain应变矩阵为

其中

3 改进BM理论
Cu基合金和Fe基合金都可以从相关文献中查到奥氏体晶系中的孪生面和孪生方向,而TiNi合金只有马氏体晶系参数.已知Ti-49.8Ni合金的孪生面qM和孪生方向eM,通过矢量操作可以得到


不变线矢x满足:

Bain应变 [BA]对不变线矢x作用后变为x1,即

需要加入转动使x和x1方向一致.建立一个坐标系统R,X轴为矢量x的方向,Y轴与x和x1都垂直,Z轴与X、Y轴都垂直,如图2所示.则坐标系统R和母相坐标系统A的基矢转换关系表示为

绕Y轴旋转一定的角度γ使x和x1重合,转动矩阵为

图2 x1矢量方向转回到x矢量方向的角度γFig.2 The rotating angle γ which changes the vector x1into the vector x

使x和x1的长度和方向都保持不变的直线不变应变

对于不变法矢n,有

令n1= [L1A′]-1·n,以x为轴旋转一定角度β使n1与n重合,如图3,转动角β是I1与I2的夹角,则转动矩阵可表示为


图3 n1法线方向转回n法线方向的角度βFig.3 The rotating angle β which changes the normal n1into the normal n
最终的直线不变应变为
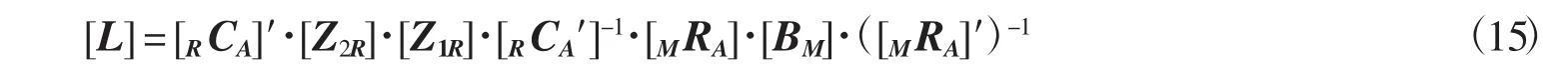
惯习面是一个不发生应变和转动的平面,L作用在简单切变面q′上,不改变切变面的方向,所以惯习面

L作用在简单切变方向e0上,可得切变方向为


4 计算结果



将本文计算结果与Matsumoto的理论数据和实验数据[7]一同列入表1中,可以看出本文所得各项晶体学参数与WLR理论值和实验值吻合度很高,说明改进BM理论可以适用于Ti-49.8Ni合金马氏体相变.

表1 数值结果Tab.1 The numerical results
5 结束语
本文改进了传统BM理论中求解直线不变应变方法,使计算过程逻辑性增强,便于编程和计算机运行计算.并利用本文提出的改进方法对Ti-49.8Ni合金马氏体相变进行晶体学计算,所得惯习面、切变方向和宏观形变量与Matsumoto利用WLR理论计算结果及实验数据吻合度高.
[1] Wechsler M S,Lieberman D S,Resd T A.On the theory of the formation of martensite[J].Trans AIME,1953,197:1503-1515.
[2] Lieberman D S,Wechsler M S,Resd T A.Cubic to orthorhombic diffusionless phase change-experimental and theoretical studies of AuCd[J].J Appl Phys,1955,26(4):473-484.
[3] Bowles J S,Mackenzie J K.The crystallography of martensite transformations(Ⅰ,Ⅱ,Ⅲ)[J].Acta Met,1954,2(1):129-137,138-147,224-234.
[4]Mackenzie J K,Bowles J S.The crystallography of martensite transformation Ⅳ.Body-centred cubic to orthorhombic transformations[J].Acta Metall,1957,5(3):137-149.
[5] 许长庆,张礼刚,路红.马氏体相变Bowles-Mackenzie理论的简化计算[J].材料热处理学报,2006,37(3):137-140.
[6] 苏慧.马氏体相变BM理论的改进算法研究[D].天津:河北工业大学,2016:25.
[7]Otsuka K,Sawamura T,Shimizu K.Crystal structure and internal defects of equiatomic TiNi martensite[J].Physica Status Solidi,1971,5(2):457-470.
[8] Knowles K M,Smith D A.The crystallography of the martensitic transformation in equaiatomic Nickel-Titanium[J].Acta Metall,1981,29:101-110.
[9] Matsumoto O,Miyazaki S,Otsuka K.Crystallography of the martensitic transformation in Ti-Ni single crystals[J].Acta Metall,1987,35(8):2137-2144.

