基于响应面法的汽车侧碰安全性优化

李梦琦，范慕辉，郄彦辉

（河北工业大学 机械工程学院，天津 300130）

0 引言

侧面碰撞是汽车交通事故中最常见的碰撞之一，相对于正面碰撞和尾部碰撞，侧面碰撞的缓冲吸能空间更小，发生碰撞时乘员更易受到较大伤害，因此汽车侧面碰撞安全性问题的研究十分必要.

针对汽车侧碰安全性问题，国内外开展了大量研究，如文献 [1]应用回归分析法对某车型进行了基于NHTSA的侧碰测试，得出了车身变形量及碰撞速度与假人胸部损伤指数间的关系；文献 [2]研究了电动车的B柱变形模式，通过对B柱上、下部分的结构强度进行分析和优化，有效降低了假人的损伤；文献 [3]通过对B柱的仿真优化设计改善了车辆的侧面碰撞安全性能，减轻了碰撞时对假人胸部的伤害；文献 [4]通过对B柱的内、外板和加强板厚度的研究，得出了胸部和腹部入侵量与入侵速度的近似模型，并应用序列二次规划方法减轻了B柱质量；文献 [5]通过对B柱内、外板和加强板的材料及厚度的优化，提高了B柱的可靠度，使车辆的碰撞安全性得到有效改善.

本文在试验验证的基础上建立某款电动轿车的侧碰仿真模型，通过对传力路径和假人胸部压缩量的灵敏度的综合分析，筛选对其侧碰安全性影响大的零部件作为设计变量进行多目标优化，在车身质量不变的同时，提高了其侧碰安全性.

1 研究模型

1.1 有限元模型的建立

首先根据厂家提供的数据建立电动轿车整车的有限元模型，整车有限元模型建立的过程主要有以下几步骤：

1）将车辆的CAD数据进行几何清理及网格划分并对网格进行质量检查.

2）根据整车的材料清单（BOM表）对各个部件赋予相应的材料及属性.

3）设置各个部件的连接，主要包括焊点、螺栓、铰链、胶粘和刚性体的连接.

4）设置模型的边界条件，主要包括接触、初始速度、刚性墙和地面.

5）设置模型的输出参数，主要包括传感器、入侵量和截面力等.

6）设置模型的控制卡片并对整车有限元模型进行检查.

整车有限元模型搭建好后，摆放ES-2假人用于测量乘员伤害值，调整壁障位置使壁障的纵向中垂面与被撞车辆的R点对齐，并定义壁障以50km/h的速度垂直撞击被撞车，完整的侧面碰撞有限元模型如图1所示.

1.2 仿真模型验证分析

按照侧碰法规（GB20071-2006） 要求对车辆进行侧面碰撞试验，对比仿真模型与实车碰撞试验车身侧面车身变形情况如图2、图3所示.

图1 侧面碰撞有限元模型Fig.1 Side impact finite element model

图2 仿真模型碰撞后侧面车身变形Fig.2 Simulation model of vehicle deformation after side impact

图3 实车试验碰撞后侧面车身变形Fig.3 Vehicle body deformation after side impact

由图2、图3可以看出仿真模型在碰撞后的车身变形与试验结果基本一致，车身变形主要集中在B柱底部及车门中下部.采集实车碰撞中右侧（非碰撞侧）B柱下端加速度曲线与仿真曲线进行对比如图4所示.

由图4可以看出，仿真曲线与试验曲线的加速度峰值分别为26.3 g和25.8 g，峰值时刻均在50 ms左右，两条曲线的变化趋势基本相同，说明仿真模型精确度较高，可以较准确的模拟试验过程并可用于优化.

1.3 假人伤害值分析

侧面碰撞中导致乘员致命或严重损伤的主要部位依次为头部、胸部、腹部和骨盆[6].因此侧面碰撞法规（GB20071-2006） 中分别规定了上述4个部位损伤指标的参考值，将试验结果中的假人伤害与仿真模型计算出的假人伤害进行对比如表1所示.

由表1可以看出，假人的胸部压缩量峰值（上肋骨）为43.12 mm，不满足法规要求的42 mm，该电动轿车需要进行改进优化.

2 侧碰关键安全部件选定

由于车辆侧面空间较小并且该车型没有配备侧气囊，所以车身结构对假人伤害的影响更加显著.为了避免在优化过程中对优化部件的盲目选取，采用传力路径分析与假人胸部压缩量灵敏度分析相结合的方法，以实现对优化部件的合理选取.

2.1 传力路径分析

车辆在发生侧面碰撞时，车门及侧围最先接触到撞击物，车门在撞击力的作用下发生内凹变形，随即将撞击力传递到防撞杆和门框；B柱作为车体侧面最主要的承载及传力结构，其在壁障侧面撞击时，将传递大量碰撞力.B柱上端将碰撞力沿车顶横梁继续传向非碰撞侧，而B柱下端可以将部分碰撞力传至门槛梁.门槛梁在侧碰过程中受到外部的直接撞击和由B柱传递作用力的共同作用，并将碰撞力沿地板及地板横梁传递到非碰撞测.侧面碰撞过程中碰撞力的传递路径如图5所示.

2.2 灵敏度分析

考虑到车辆侧面结构件较多，若逐一对侧面结构件进行优化，势必会增加不必要的工作量.因此选取在侧碰中主要的承载与传力的部件作为研究对象，采用正交试验法建立二阶响应面进行分析，研究相关部件对假人胸部压缩量的敏感程度，判断各影响因素的主次.

如图6所示，选取了8个侧碰中的主要部件，通过改变所选部件的材料，分析对假人胸压的改善情况，选出对胸压改变较敏感的部件，再对该部件的材料和厚度进行多目标优化.

2.2.1 试验设计及因素水平选取

正交试验设计方法（Orthogonal arrays）是用正交表安排多因素试验的一种高效、快速的试验设计方法.采用正交试验的设计方法分析侧面相关部件对假人胸压影响的贡献率，可以合理安排因素水平、保证试验精度的要求并考虑交互作用的影响.

选择侧碰中的8个主要部件作为设计变量，选择屈服强度高、中、低的3种材料作为设计变量的3水平，材料相关参数如表2所示.

图4 右侧B柱下端加速度对比Fig.4 Comparison of acceleration at the lower end of the right B-pillar

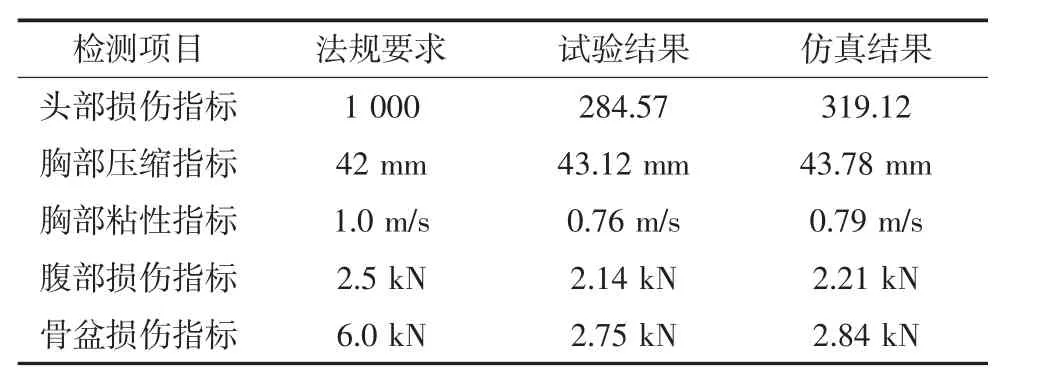
表1 侧碰假人损伤指标试验值与仿真值对比Tab.1 Comparison of the test results and simulation values of the damage index of side impact dummy

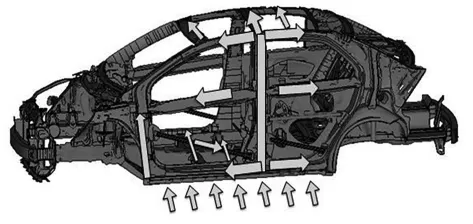
图5 侧面碰撞力的传递路径Fig.5 Transmission path of side impact force

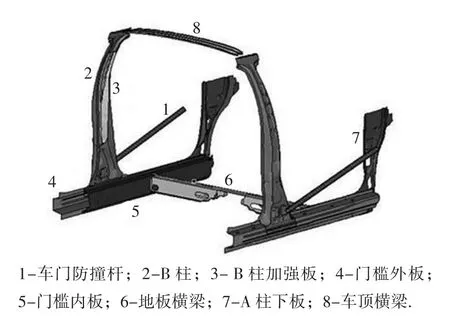
图6 侧面碰撞中主要部件Fig.6 Main components in side impact

表2 材料相关参数Tab.2 Material parameters

通过对侧面传力路径分析筛选出8个主要部件作为假人胸部压缩量的灵敏度分析对象，每个分析对象选取3水平进行试验设计，最终得到8因素3水平的L27（38）正交表如表3所示.

表3 正交试验水平因素表Tab.3 Orthogonal test level factor table

2.2.2 试验结果及分析

根据8因素3水平的正交表，设计了27组试验方案并依次修改仿真模型进行计算，得出假人胸部压缩量（RDC） 峰值，正交试验表及仿真计算结果见表4.

根据正交试验结果可以建立应变量的二阶响应面模型，通过方差分析可以获得Pareto图和主效应图.Pareto图即贡献率图，可以反映拟合后模型中各个设计变量对响应的贡献程度百分比.主效应图即设计变量的变化引起目标参数变化的趋势图，通过对主效应图的分析可以反映各个设计变量的改变如何影响目标参数[7].所以，根据Pareto图和主效应图可以为后期优化提供明确方向.根据仿真计算结果建立假人胸部压缩量的二阶响应面模型，其Pareto图和主效应图如图7、图8所示.

表4 正交试验设计结果Tab.4 Results of orthogonal test design

图7 设计变量对胸部压缩量的贡献率Fig.7 The contribution of design variables to chest compression

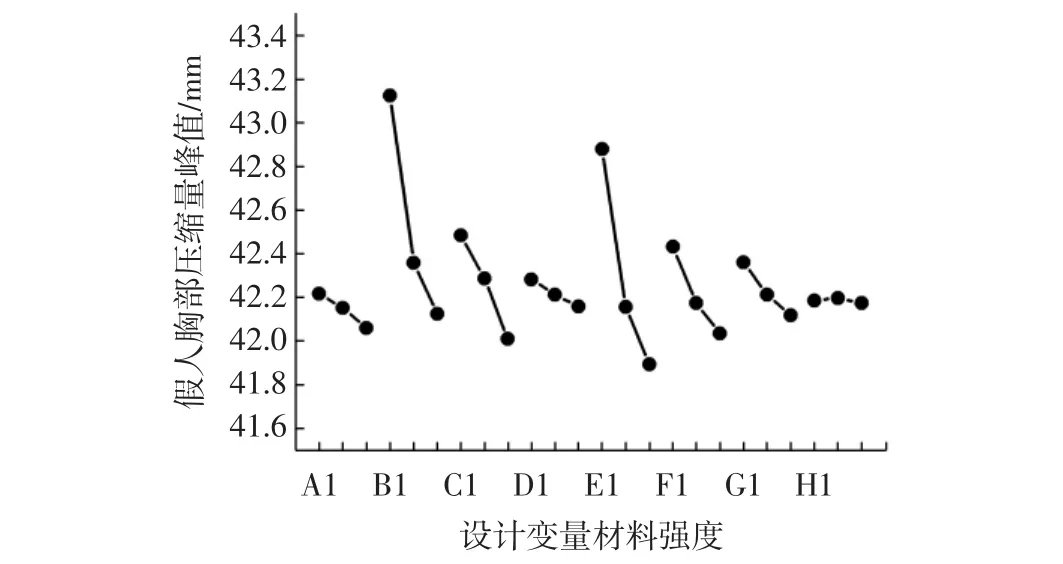
图8 设计变量对胸部压缩量的主效应图Fig.8 The main effect of design variables on chest compression

根据Pareto图可以看出编号B、C、E、F的设计变量即B柱、B柱加强板、门槛内板、地板横梁对假人胸部压缩量的贡献率较高，是影响假人胸部伤害的主要因素，根据主效应图可以看出在提高设计变量强度的情况下，胸部压缩量均有明显的下降，即主效应为负.同时，从胸部压缩量峰值的变化量可以发现，通过提升相关部件的材料强度胸部压缩量峰值没有显著的降低，说明仅仅提升相关部件的材料强度并不能使胸部压缩量达到安全指标.

综上所述，根据灵敏度分析结果，选取对侧碰中假人的胸部压缩量影响最为显著的B柱、B柱加强板、门槛内板、地板横梁作为设计对象，在考虑材料强度的同时引入结构厚度作为设计变量，为减小假人胸部压缩量作进一步优化.

3 侧碰关键安全部件优化设计

根据灵敏度分析选出对侧碰中假人的胸部压缩量影响较大的部件作为设计对象，采用试验设计的方法建立二阶响应面近似模型，对材料与厚度进行混合优化寻找最优解，并在降低假人侧碰中胸部压缩量的同时考虑到优化构件的质量增加情况，实现质量不增加及胸部压缩量减小的多目标优化.

3.1 设计变量及设计目标

选取B柱、B柱加强板、门槛内板及地板横梁的材料和厚度作为设计变量，材料依旧选取屈服强度较高、中等、较低的3种材料即B340/590DP、B210P1、DC04，厚度选取范围为0.5～2.5 mm.设计变量及变量选取范围如表5所示.

优化过程中考虑到侧面结构的安全性，引入车门及B柱的入侵量和入侵速度作为约束条件，以设计变量的总质量最小及假人胸部压缩量峰值最小为设计目标.侧碰中假人胸部伤害优化问题的数学模型可定义为

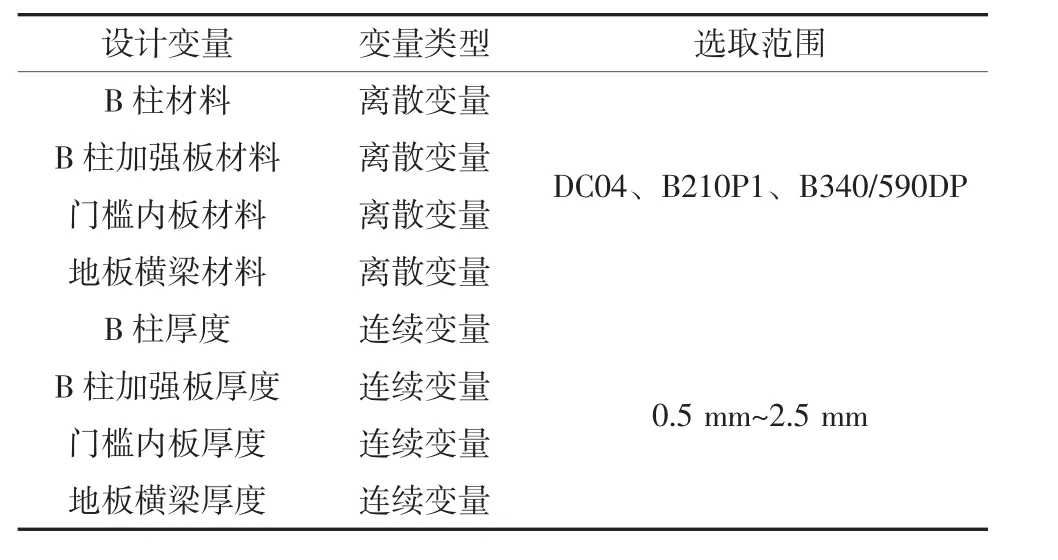
表5 设计变量及选取范围Tab.5 Design variables and selection

式中：Mass为4个设计变量的总质量；RDC为假人胸部压缩量峰值；disD为车门入侵量峰值；disB为B柱入侵量峰值；vD为车门入侵速度峰值；vB为B柱入侵速度峰值；ti为各构件的厚度.

3.2 近似模型的建立

近似模型方法是通过数学模型逼近设计变量与响应变量的方法.常用的近似模型有响应面（Response Surface Method，RSM） 模型、克里格 （Kriging） 近似模型和径向基 （Radial Basis Function，RBF） 模型[8].本文使用的响应面近似模型，通过较少的试验样本在设计空间内较为精确的逼近函数关系，可以拟合复杂的响应关系，具有良好的鲁棒性[9-10].

采用优化的拉丁超立方试验设计方法，在设计空间中均匀采集了90组设计样本，并通过仿真软件计算出样本的输出响应.通过计算结果建立假人胸部压缩量峰值及设计变量总质量的近似模型，并在样本集合中随即抽取10个样本进行近似模型的误差分析，如表6所示；假人胸部压缩量峰值和设计变量总质量的预测及仿真关系见图9、图10.

根据表6可以看出，胸部压缩量峰值和设计变量总质量近似模型的决定系数R2分别为0.997 8和0.979 4，修正的决定系数分别为 0.991 4和0.974 7，均大于工程预测要求的0.9，表明响应面近似模型的拟合程度较好.

表6 近似模型的误差分析Tab.6 Error analysis of approximate model

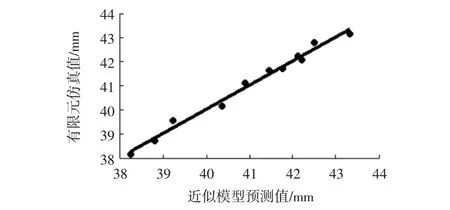
图9 假人胸部压缩量峰值的预测与仿真关系Fig.9 Prediction and Simulation of peak value of chest compression for Dummies

由图9、图10可以看出，通过近似模型预测的假人胸部压缩量峰值和设计变量总质量与仿真计算的结果十分接近，再次说明响应面近似模型的拟合程度较好.

3.3 优化过程及结果分析

考虑到同时优化设计对象的材料和厚度，属于混合变量多目标优化问题.因此，本文采用非支配排序遗传算法NSGA-II对建立的响应面近似模型进行多目标优化，NSGA-II具有求解Pareto解集准确性及分散性较好的优点.遗传算法参数设置为：种群规模为100、杂交概率为0.9，变异概率为0.05，进化代数为50；获得多目标优化的Pareto前沿图，如图11所示.

由图11可以看出，Pareto前沿较为平滑，覆盖了大量的最优解集.由于假人胸部压缩量峰值与设计变量总质量为相互矛盾的优化目标，所以不可能使多目标同时达到最优解，需要对多个目标之间进行协调处理.在保证设计变量总质量不增加的前提下，尽可能使假人胸部压缩量峰值最低，选取的最优方案如表7所示.

根据表7可以看出，选取的优化方案中假人胸部压缩量峰值为36.24 mm，下降了15.9%；而设计变量总质量为15.29 kg，相比初始设计值无质量增加.

3.4 整车碰撞试验验证

根据优化方案对车辆进行改进，按照侧碰法规（GB20071-2006） 要求对车辆再次进行侧面碰撞试验，提取优化前、后假人胸部上肋骨压缩量曲线进行对比，如图12所示，优化后的假人胸部上肋骨压缩量峰值明显降低，为36.72 mm，相比优化前下降了14.8%.

采集前排假人各项伤害指标并与优化前的试验结果进行对比，如表8所示，优化后的假人各项损伤均有所降低并满足侧碰法规要求，实现了在保证车身质量不变的前提下提高侧碰安全性的目标.

图10 设计变量总质量的预测与仿真关系Fig.10 Prediction and Simulation of total mass of design variables

图11 Pareto前沿图Fig.11 Pareto front view

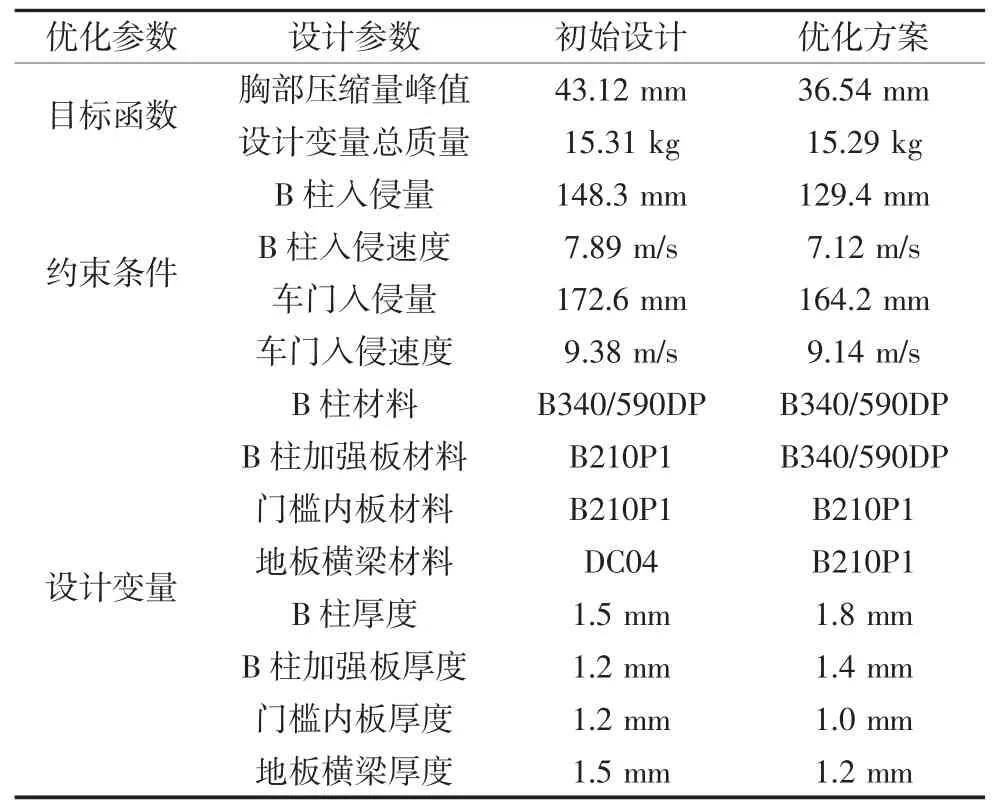
表7 初始设计与优化方案对比Tab.7 Comparison of initial design and optimization

图12 优化前、后假人胸部上肋骨压缩量对比图Fig.12 Comparison of the compression of the upper chest of the dummy before and after

4 结束语

1）建立了符合侧碰试验结果的有限元模型，通过对侧面碰撞传力路径的分析，初选侧碰中主要的承载与传力的部件，再通过假人胸部压缩量的灵敏度分析，筛选出对假人胸部压缩量影响较为显著的关键部件作为优化对象，减少了后续优化的设计变量个数，提高了优化的效率.

2）采用拉丁超立方试验设计方法对关键部件的材料及厚度进行试验设计，建立了设计目标的二阶响应面近似模型，并对其进行误差分析保证了近似模型的拟合精度.

3）针对多目标的优化问题，采用非支配排序遗传算法NSGA-II对近似模型进行优化获得Pareto最优解集，在保证设计变量总质量不增加的前提下选取最优方案并进行整车碰撞试验验证，试验结果显示假人胸部压缩量峰值明显减小，各项损伤指标均满足侧碰法规要求，说明该方案具有较高的准确性与有效性，在保证车身质量不变的同时，实现了侧碰安全性的提高.

表8 优化前、后假人各项损伤指标对比Tab.8 Comparison of the dummy injury index before and after optimization

[1] 梁韫.基于某车型的侧面乘员约束系统开发方法研究[D].长春：吉林大学，2013.

[2] 陈新.基于顶压及侧碰安全性的B柱结构优化设计[D].长沙：湖南大学，2012.

[3] 胡远志，黄杰，刘西，等.某车型正面碰撞后排乘员伤害的仿真优化[J].科学技术与工程，2015，15（7）：259-264.

[4] 徐增密，刘立忠，申国哲，等.基于响应面和kriging代理模型的汽车B柱优化设计[J].汽车技术，2012（4）：39-43.

[5] 朱敏，姬琳，叶辉.考虑侧碰的汽车B柱加强板材料性能梯度优化[J].吉林大学学报（工），2011，41（5）：1210-1215.

[6] 苏国峰.基于CAE技术的汽车侧面帘式气囊模块设计[D].长春：吉林大学，2007.

[7] 侯淑娟，谭伟，韩旭，等.一种汽车车身多变量抗撞性优化设计的变量筛选方法：CN 103279598 A[P].2013.

[8] 许辉，周奇.多学科优化中的近似模型及其在艇体结构优化中的应用[J].舰船科学技术，2014，36（12）：6-10.

[9] 谷传文，孙丽娟，李晓东，等.径流叶片扩压器的气动设计与优化[J].流体机械，2016（5）：22-25.

[10]万利军，单炜，姜华.基于响应面法的桥梁动力学有限元模型修正[J].公路交通科技，2014，31（8）：96-101.