观察代数结构特征 体会数学模型思想——基于数学能力发展下的数学例习题教学模式研究

林 美

（福州屏东中学，福建 福州 350001）

“模型思想是一种重要的数学基本思想之一，在初中教学中融入模型思想，不仅能够优化学生的数学知识结构，而且能指导学生探索解题思路，提高学生的思维品质。数学教学中应从概念出发，深入探究其内涵，挖掘其本质，在解题时从概念出发，思考概念所涉及到的外延，这样往往会水到渠成。”［1］

一、抓住代数的结构特征，巧解一类方程题

观察代数结构特征，可以有效突破一类数学难题。学生觉得题目难，关键就是题目的形式不熟悉，题目的参数多。这个难点的突破口就是把握式子本身的结构特征，用整体的思想去看待某个式子，利用模型思想将未知问题转化为已知问题。在教学人教版七年级下二元一次方程组的习题课时，笔者就对一道课例进行题组变形，让学生体会代数的结构特征，从而学会抓住解题的本质。

分析：难点突破观察式子的结构特征就会变繁为易，变难为简，该道题把（x-2）和（y+3）分别看成两个整体，可得x-2=，y+3=，则方程组的解是

抓住问题的关键，继续进一步变式：

穷追不舍，继续挖掘式子的结构特征，多参数的计算，可以让学生进一步思考问题。

求下列关于x，y的方程组的解？方程组的变式如下：

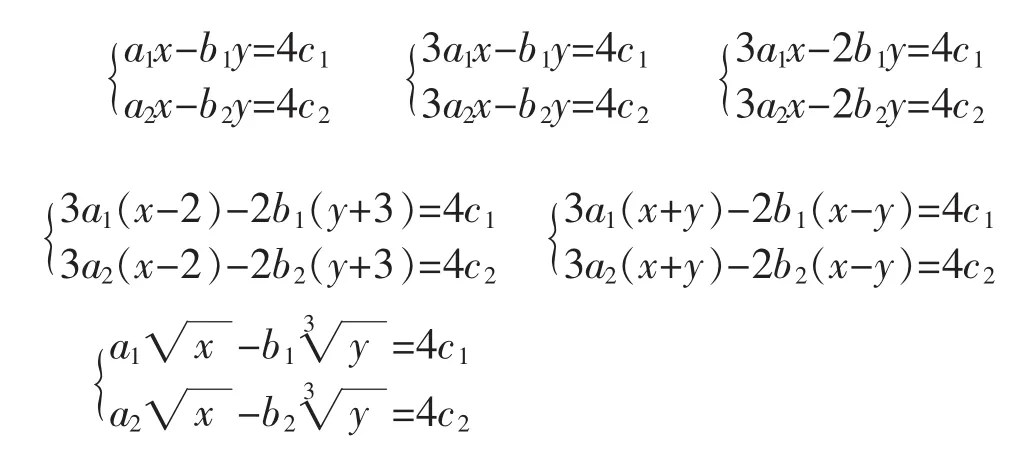
课堂上，笔者常通过这一类题目，让学生找到共同特点：抓住式子的结构特征进行转化，把未知转化为已知的模型思想进行解答。这样的题组训练，对于学生深入挖掘题目内涵和外延，对于知识体系的建构，思维的拓展都起到很好的效果。

二、抓住代数的结构特征，挖掘新概念的生成过程

很多情况下，作为一线的教师本身就没有理解为什么要引入新的知识点，没有花心思去思考新概念生成的过程，更不会去体会新概念的存在意义和价值。

可以思考这样一个问题，为什么要学习整式，这章在初中学习的作用和意义。其本质就是从数到字母的一个生成过程。深刻体会用字母或含有字母的式子表示数和数量关系在数学上的重要作用，让学生学会观察代数的结构特征，在教学中让学生不断体会概念的生成过程，在生成过程中挖掘其共性，这样的教学就会更加有意义。下面以“同类项的定义”这个概念生成过程来体会从数到字母的转化的必要和联系。

例2观察下面式子：

（1）运用运算律计算：

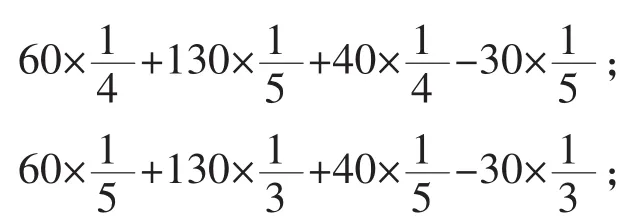
（2）根据（1）中的方法完成下面的运算，并说明其中的道理：

60a+130b+40a-30b

式子本身有相同的结构，并且用字母a，b代表一个因（乘）数。这样就水到渠成找到了类，进而引出同类，发现同类项的定义。学生在观察式子的结构的过程中，牢牢抓住式子的结构特征，不断体会从数到字母的转化过程，了解字母式本身的意义从而引出新概念。

教师不断引导学生去挖掘概念的生成过程，才能让学生体会知识本身存在的意义，也为代数知识的建构，内化知识提供有效的方法。一线教师实实在在地去研究课本，从课本的内涵出发，引出新的概念，不断渗透数学的思想和方法，让学生在解题中触类旁通。

三、抓住代数的结构特征，突破定势思维

学生的学习是一个不断探索的过程，而在此过程中怎样学习是重中之重。学生在遇到题目时总是很难从式子中观察出其内在联系，无法把未知的形式转化为已知的形式。抓住代数的结构特征，在最近学习区域去找已知的知识点，在中考复习中就显得尤为重要。

以一道一元二次方程根与系数的关系的习题课，突破中考的难题，中考题源于课本，高于课本。一线教师只有在新课教学过程中层层渗透数学模型思想，学生才会在面对题目时临危不惧。在一元二次方程根与系数关系第二课时，以下面题组形式让学生思考一类问题：

学生的常规做法就是算二次根式得到结果，不妨引导学生观察式子的结构特征，发现上面的算式可以分解两个式子，其形式与一元二次方程的根的结构类似，就是公式法解一元二次方程的根，再进一步观察发现就是是一元二次方程2x2+5x+3=0的两根之和。这道题就迎刃而解。

进一步思考这类问题，进一步变式求值：

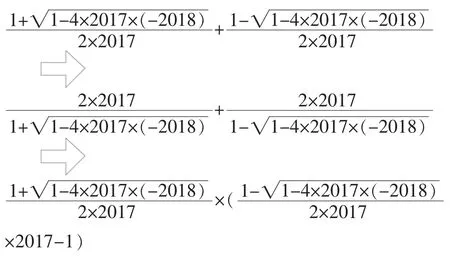
题组呈现，让学生学会观察式子的结构特征，可以找到式子背后最本质的含义。初中代数的学习就是充分理解知识本身的内部结构，再去看一类中考题，发现它难在考察了代数本身的结构特征，代数的转化思想和模型思想，为解决多参数的题目提供了帮助。

例 4（2014年福建厦门）设 a=192×918，b=8882-302，c=10532-7472，则数 a，b，c 按从小到大的顺序排列，结果是

解：从式子的结构特征去估算a，b，c的值，a=192×918=361×918，b=8882-302=（888-30）（888+30）=858 ×918，c=10532-7472=（1053+747） （1053-747） =1800×306=600×918．

例5（2017年福建）若直线y=kx+k+1经过点（m，n+3）和（m+1，2n-1），且 0

这些题目都是抓住代数结构特征，去认识它就是因式分解和不等式的综合题。

四、抓住代数结构特征，建立数学模型

教师在代数的教学中，不仅让学生学会观察代数的结构特征，训练学生抽象概念的能力，而且培养学生利用转化思想，使实际问题数学化，数学问题实际化，用数学的眼光去看世界，用数学的语言去表达世界，为适应社会打下坚实基础。

“著名的数学家戈尔丁认为，为了了解周围世界，人们把自己的观点以及思想组织成概念的体系，这种概念体系就是模型。”［2］而用数学的语言、方法对各种对象着眼于模型思想、应用意识、创新意识和应用能力等方面来探讨初中方程教学，深入发展代数结构特征的研究，建立模型的过程就成为数学建模。我国的《九章算术》中有很多数学模型（如：方田、方程、衰分、勾股等），它的理论版块有：“题”“答”“术”，其中“术”是解决问题的方法，即数学建模。由此得知，数学模型起源于生活经验，起源于社会实践活动。［1］方程的教学中融入数学建模活动和模型思想，能够培养学生的创新能力与应用意识。学生在学习中就会调动学习的的积极性和主动性，不断激发学生的数学学习兴趣。

例6：（2017年福建）我国古代数学著作《孙子算经》中有“鸡兔同笼”问题：“今有鸡兔同笼，上有三十五头，下有九十四足，问鸡兔各几何？”其大意是：“有若干只鸡和兔关在同一笼子里，它们一共有35个头，94条腿，问笼中的鸡和兔各有多少只？”

建模循环强调了建模过程作为循环重复的形式出现,布鲁姆（Blum）和凯瑟梅斯默（Kaiser-Messmer）提出的循环过程是许多相似观点的典型，［3］如下图：

布鲁姆和凯瑟梅斯默的建模循环

尝试着在现实情境中寻找数学模型，用数学的思维思考情境，把生活语言转化成数学语言，把实际问题转化成数学问题：

《义务教育数学课程标准（2011年版）》强调如何调动学生学习的积极性，如何让学生学会深层次的思考，如何鼓励学生的思维创造性？这就是需要教师在数学的课堂教学中不断去渗透。用方程解决实际问题是重要教学内容之一。实际问题的教学就是数学建模活动的素材，让学生把生活问题用数学的眼光去看，用数学的思维去解决，渗透着典型的模型思想。面对多元的世界，一线教师更要让学生体会数学的真正价值，能用数学的知识体系去看世界，用数学的思想方法去判断世界，能解决生活中的实际问题.

数学的教学过程中贯穿着数学基础知识和数学思想方法。特别强调数学的思想方法是数学知识的精髓和数学的灵魂。它往往被忽视，没有发挥应有的价值。对于学生，要学会数学所蕴含的思想方法，形式数学素养，体会数学对于人类文明发展的贡献，形成正确的世界观、人生观和价值观，彰显数学育人的价值。一线教师就是在不断挖掘课本内涵，不断突破自己教学的困惑。教师就要做到不断学习发展，不要停留在知识的层面，在教学中要有足够的视野，才能在教学中深入浅出，有的放矢。在教学中不断给学生恰当的问题，恰当的情境，恰当的机会，给学生足够的空间，在某个困惑中不断思考、尝试、探索、挖掘，把这个困惑变成知识技能，形成自己的能力，发展自己的数学素养。

［1］于莉.基于模型思想的初中方程教学设计研究［D］.重庆：重庆师范大学，2013．

［2］张茹静.数学模型思想与中学数学应用教学之研究［D］.西安：陕西师范大学，2002．

［3］童永健.高中数学教材中数学建模内容的分析及再设计［D］.上海：华东师范大学，2016.