采用BP神经网络预测钻削灰铸铁的切削能耗

， ，

(福建工程学院 机械与汽车工程学院， 福建 福州 350118)

机床是广泛应用于制造业的生产设备之一，He等人[1]认为机床的效率低于30%，并且机床在零件加工过程中对环境的影响99%以上是由电能消耗所引起。切削能量消耗预测模型可以为机床加工过程的能耗定额制定、切削工艺参数节能优化、能效评估等提供一定的数据支持。机床

加工能耗预测有数值、经验和人工智能等方法。Sangwan等人[2]利用有限单元法、有限差分法、边界元法等建立了数值模型。谢东、陈薇薇等人[3-4]利用BP神经网络对数控机床切削能耗进行建模预测。Zeng Y R等人[5]利用自适应微分进化算法支持的反向传播神经网络模型来估计能量消耗，结果表明，此模型能够有效地预测能量消耗。邱行[6]则在工件加工过程切削能耗综合预测模型的基础上，开发出软件化的基于指数切削能耗模型。但数控机床部件繁多，机床加工能耗复杂，影响机床加工能耗的相关联因素众多，使得机床加工能耗的预测和建模变得相当困难[7]。

灰铸铁具有切削加工性能良好、耐腐蚀等特点，在生产中广泛应用。本文采用BP神经网络建立灰铸铁钻削过程的切削能耗与切削参数之间的关系模型，同时建立三元线性回归预测模型，对比两种预测模型的预测结果的准确性，并考虑切削参数之间的交互作用建立三维表面图，对比分析钻削过程的切削能耗与切削参数的变化规律，为实际钻削加工节能减排提供理论和实际指导。

1 试验条件与设计

1.1 试验材料与设备

采用灰铸铁HT200为试验材料，进行钻削试验研究。试样尺寸为85 mm×64 mm×20 mm。机床设备为MCV-810加工中心，主轴最高转速8 000 r·min-1，机床最大功率为20 kVA，面板是FANAC数控系统。功率测量设备采用WT330系列功率仪。钻削刀具采用YG6X硬质合金麻花钻，试验加工功率测试平台如图1所示，加工过程中使用切削液，所加工的孔为通孔。

图1 钻削加工功率测试平台Fig.1 Drilling power test platform

1.2 试验设计

采用全因素试验方法进行钻削试验，钻削参数如表1所示。试验组数为64组，每组钻削参数组合重复3次然后取平均值。

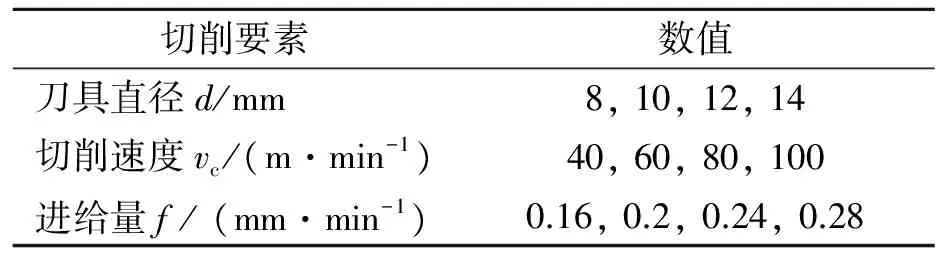
表1 试验参数

1.3 试验结果

图2为加工中心MCV-810在加工参数d=8 mm、vc=60 m·min-1、f=0.16 mm·r-1时的钻削功率曲线，钻削过程的总加工功率由待机、空载及切削功率组成，本文研究的切削能耗为切削功率与钻孔时间的乘积，如公式(1)和(2)所示。

(1)

Ec=Pc×Tc

(2)

式中，Tc为钻单个孔所用时间，min；Id为钻孔深度，mm；n为主轴转速，r·min-1；Ec为切削能耗，J；Pc为切削功率，W。

图2 加工中心MCV-810钻削功率曲线Fig.2 Drilling power curve of MCV-810

2 切削能耗预测模型建立

2.1 确定BP神经网络结构

随机初始化一组网络连接权重和阈值。然后，使用训练样本调整网络连接权重和阈值。经过反复学习训练，当网络输出值和训练样本的均方误差(MSE)达到误差目标时，调整过程终止。BP算法是一个很有效的算法，许多问题都可由它来解决，其算法程序如图3所示[8]。

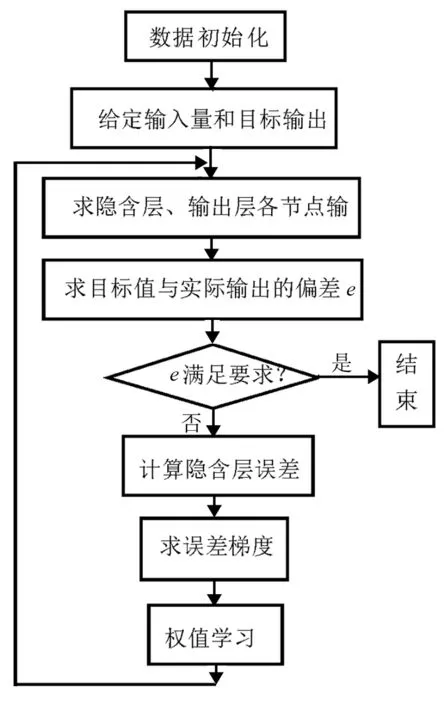
图3 BP神经网络算法程序框图Fig.3 Flow chart of BP neural network algorithm

BP神经网络通常采用三层结构，分别为输入层、隐藏层和输出层，它们互相连接，各层的每个神经元都会连接到下一层的所有神经元。如图4所示，本文BP神经网络结构的输入层为切削速度、进给量和刀具直径，输出层为切削能耗，中间层为隐藏层，隐层节点数目需合理，实际中应用公式来确定。根据前人经验，参照式(3)设计。

(3)

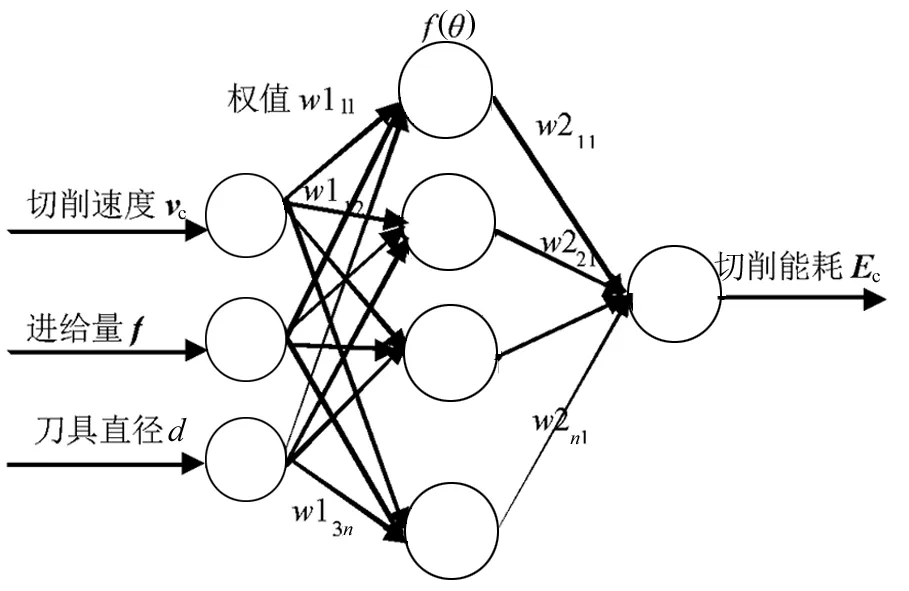
图4 BP神经网络结构Fig.4 BP neural network structure

其中，L为隐层节点数;m为输入层节点数;n为输出节点数;a为[0,10]之间的常数,一般取3～6。

2.2 确定BP神经网络样本

预测样本可以有规律地选择。因为刀具直径的大小对切削能耗的影响较大，而且切削速度和进给量对切削能耗的影响规律不一样，因此考虑每种刀具直径选择4组，切削速度以40、60、80、100 m·min-1分4组，进给量以0.16、0.2、0.24、0.28 mm·r-1每一大组循环，由此得到16组预测样本。每种切削速度和进给量的数据一样多，其余48组作为训练样本。

2.3 建立和训练BP神经网络

在训练和测试之前，为了数据处理的方便，保证程序运行收敛加快，采用premnmx函数将输入数据归一化到-1～1。隐层中的tansig传递函数和输出层中的purelin传递函数用于映射切削能耗值。选择trainscg量化共轭梯度算法训练函数作为实现BP神经网络训练功能。根据式(3)隐层节点在5～8，通过BP神经网络误差的比较，当隐层节点为8时误差最小，由此将BP神经网络隐层节点数取为8。进行BP神经网络基本训练参数设定，网络最大迭代次数为10 000次，学习速率为0.05，次数显示间隔为50，目标误差为10-3，二次求导对权值调整的影响参数为5.0×10-5，Hessian矩阵不确定性调节参数5.0×10-7，均方误差为1.0×10-4。

如图5所示，均方误差随着迭代次数的增加而减小，直到243次迭代停止。测试数据的预测值与实验值之间的相关系数R为0.999 83，如图6所示，显示其拟合效果很好，刀具直径、切削速度、进给量和切削能耗之间存在很强的相关性。由图7可以看出测试样本切削能耗实验值和预测值较为一致。保存使用所选参数训练好的BP神经网络模型，调用网络模型将整体64组试验样本代入进行预测，图8其R值为0.999 54。

图5 均方误差(MSE)随时间的变化Fig.5 Variation of mean square error (MSE) over time

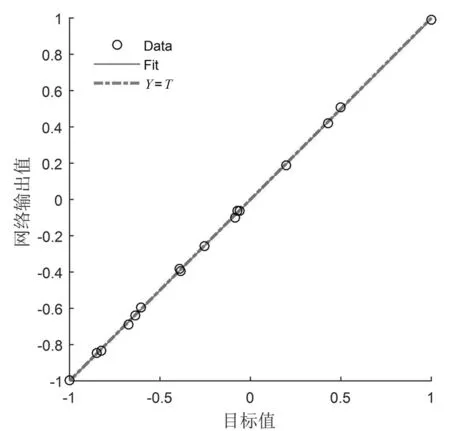
图6 预测值与测试数据之间的相关性Fig.6 Correlation between the predicted value and the test data

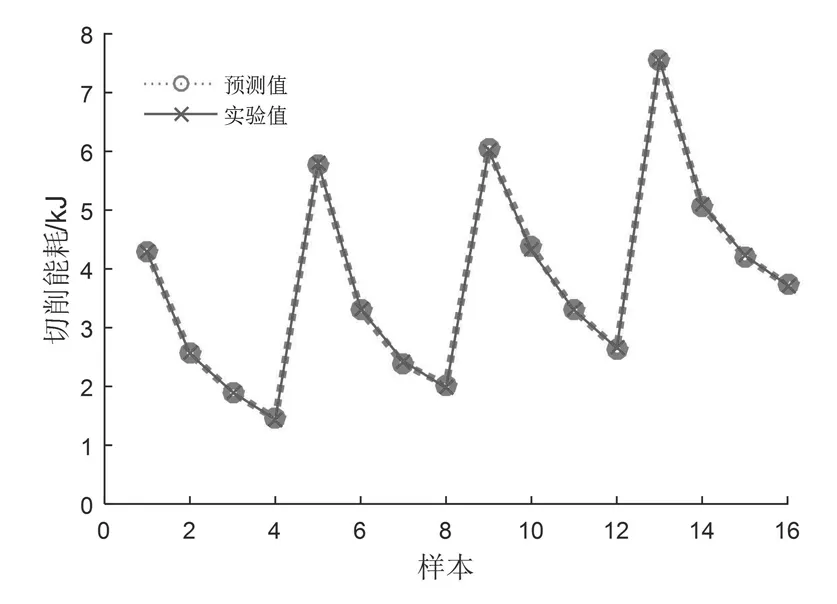
图7 切削能耗实验值和预测值的比较Fig.7 Comparison of experimental values and predicted values of cutting energy consumption

图8 预测值与全部数据之间的相关性Fig.8 Correlation between the predicted value and the total data

图9 切削能耗三元回归Fig.9 Ternary regression of cutting energy consumption

2.4 切削能耗三元线性回归预测模型的建立

对钻削过程的切削能耗进行三元回归拟合，分析刀具直径、切削速度、进给量对钻削过程切削能耗的影响。经过拟合分析，得到如图9所示切削能耗三元线性回归图，并建立钻削过程的切削能耗三元线性回归预测模型，如式(4)所示。其相关系数R2是检测三元线性回归预测模型的重要指标，其值越接近于1,表明所建立的预测模型拟合效果越好。式(4)的R2值为0.970 86，说明所建立的三元线性回归预测模型拟合效果很好，可以用于钻削过程切削能耗的预测。由式(4)可看出，切削能耗随刀具直径的增加和进给量、切削速度的降低而变大，其影响主次为d>f>vc，f和vc

对切削比能耗的影响都为正效应，且程度相当，而d则呈负效应。

Ec=0.643 01d1.251 58vc-0.551 46f-0.660 12

(4)

3 试验结果与分析

3.1 切削能耗预测模型误差分析

根据BP神经网络和三元线性回归预测模型，可预测出64组试验的切削能耗。在此列出神经网络测试样本的16组试验数据、预测结果及相对误差对比，如表2所示。经过比对分析，神经网络预测值相对误差比较小,都在1.5%之内，其平均相对误差为0.635%，三元回归预测值相对误差最大为14.133%，其平均相对误差为5.793%。根据图10也可看出,切削能耗的实测值与BP神经网络预测值的曲线非常贴近，而三元回归的预测值则有点偏离，由此说明BP神经网络预测模型预测值的精度和稳定性明显比三元线性回归预测模型高，通过训练的BP神经网络在预测切削能耗方面具有良好的准确性，对钻削过程的切削能耗预测研究具有一定应用价值和指导意义。

表2 试验数据、预测结果及相对误差对比Tab.2 Test data, predicted results and comparison of relative errors

3.2 切削参数对切削能耗的影响分析

由图10可看出,刀具直径、切削速度、进给量对切削能耗的影响趋势与三元回归预测模型的指数完全一致。图11为64组整体样本范围内BP神经网络切削能耗预测值与切削参数之间的三维表面图，其只固定一个而同时考虑两个切削参数对切削能耗的交互作用。从图11(a)可看出，同时提高进给量和切削速度，切削能耗反而降低。在刀具直径固定的情况下，切削参数值越高，机床会输出更高的负载，切削能耗理应越大，但此种情

况下，随着切削参数值的增加，能耗反而急剧下降。这表明加工时间主导着能源消耗，切削参数值越高，材料去除率就会越大，加工时间反而缩短，最终导致切削能耗降低。图11(b)vc=60 m·min-1和图11 (c)f=0.2 mm·r-1都与刀具直径有交互作用，增大刀具直径,切削能耗急剧增高，可见刀具直径对切削能耗有很大的影响，但实际加工中考虑刀具直径对切削能耗的影响意义不大。因此从减小切削能耗的角度分析，在满足加工质量前提下，钻削灰铸铁时优先选择较大的进给量和切削速度更有利于节能降耗。

(a)vc=60 m·min-1, f=0.24 mm·r-1

(b)d=8 mm, f=0.24 mm·r-1

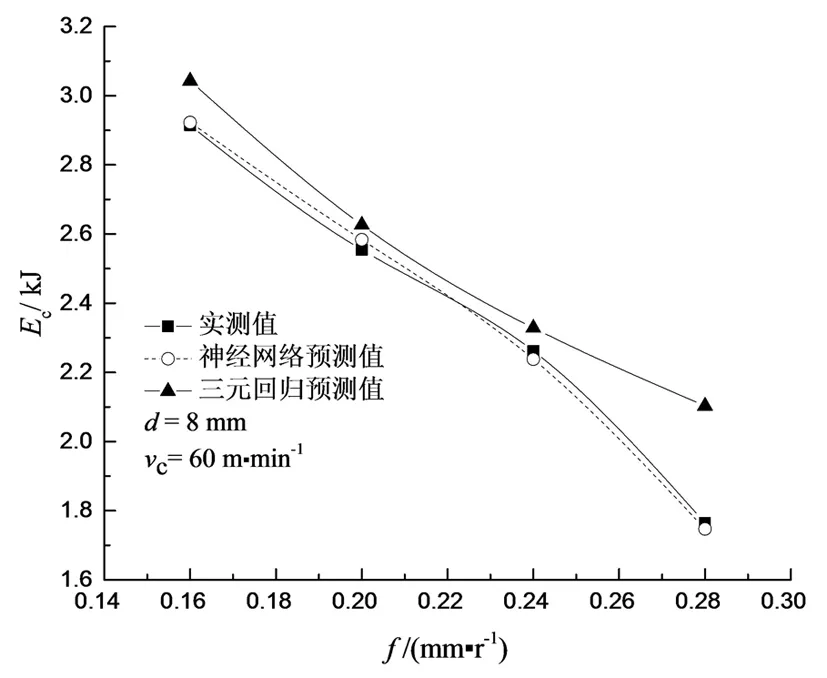
(c)d=8 mm, vc=60 m·min-1图10 切削参数对切削能耗实测值和预测值的影响Fig.10 Effect of cutting parameters on the measured and the predicted values of cutting energy consumption

(a) d=8mm

(b) vc=60 m·min-1

(c) f=0.2mm·r-1图11 BP神经网络预测值与切削参数之间的三维表面图Fig.11 Three-dimensional surface graph between BP neural network predictions and cutting parameters

4 结论

1)采用BP神经网络模型对钻削过程的切削能耗进行预测。将BP神经网络预测模型与三元线性回归预测模型进行比较发现，BP神经网络预测模型的预测值相对误差较小,都在1.5%之内，其平均相对误差为0.635%，其预测精度和稳定性均比三元线性回归预测模型高，说明通过训练的BP神经网络模型能较准确地预测切削能耗，对钻削过程的切削能耗预测研究具有一定应用价值和指导意义。

2)通过切削参数对灰铸铁钻削过程中切削能耗实测值和预测值的影响分析，切削能耗随刀具直径的增加和进给量、切削速度的降低而变大。在刀具直径不变情况下，随着切削参数值的增加，能耗急剧下降，加工时间主导了能量消耗，即使在较高负荷的情况下，总能耗也会降低。因此从减小切削能耗的角度分析，在满足加工质量的前提下，钻削灰铸铁时应优先选择较大的进给量和切削速度更有利于节能降耗。

[1] He Y, Liu B, Zhang X, et al. A modeling method of task-oriented energy consumption for machining manufacturing system[J].Journal of Cleaner Production,2012,23(1):167-174.

[2] Sangwan K S, Kant G, Deshpande A, et al. Modeling of Stresses and Temperature in Turning Using Finite Element Method[J].Applied Mechanics & Materials,2013,307: 174-177.

[3] 谢东,陈国荣,施金良,等.基于BP神经网络数控机床切削能耗的研究[J].机床与液压,2012,40(1):54-57.

[4] 陈薇薇,张华,向琴,等.基于支持向量机数控机床切削能耗预测方法研究[J].机械设计与制造,2014(11):54-56.

[5] Zeng Y R, Zeng Y, Choi B, et al. Multifactor-Influenced Energy Consumption Forecasting Using Enhanced Back-propagation Neural Network[J]. Energy,2017，127:381-396.

[6] 邱行.工件加工过程切削能耗的预测方法研究及应用系统开发[D].重庆：重庆大学,2016.

[7] Kant G, Sangwan K S. Predictive Modeling for Energy Consumption in Machining Using Artificial Neural Network[J]. Procedia Cirp,2015,37:205-210.

[8] 胡伍生.神经网络理论及其工程应用[M].北京：测绘出版社,2006:63-76.