锅炉管阵列中的声二极管效应与冷态缺陷研究
刘月超, 姜根山, 许伟龙, 孔 倩
(1. 华北电力大学 能源动力与机械工程学院, 北京 102206;2. 华北电力大学 数理学院, 河北保定 071003)
电站锅炉换热器(如水冷壁、过热器、再热器和省煤器)管道泄漏事故已成为影响火电机组经济安全运行的重要因素.近年来,声学检漏利用声波信息进行泄漏判断与检测,具有实时性、可远程监测和可应用于炉内高温、高压环境等优点,采用声学方法检测管道是否泄漏已成为近年来电站锅炉故障诊断技术最具发展潜力的方法之一.但由于其理论基础研究滞后,这项技术发展较为缓慢.且由于电站锅炉管阵列环境和结构的复杂性,泄漏的声传播受到管阵列的阻挡,其泄漏声源的频谱规律以及声压辐射指向性特征均发生极大的变化,对管道内泄漏位置的检测与定位造成极大干扰[1-5],使声学检漏技术存在误报、漏报情况,因此研究炉内管阵列的声传播特性与辐射特性对炉内泄漏声源的定位具有重要意义.
基于之前的研究,当声波通过某一管阵列时存在声波禁带与导带,温度场会对声传播产生影响的现象[6-9],笔者对不同管阵列的声传播特性进行研究.锅炉运行时,管阵列处于高温环境,当某根管发生泄漏时,其中的水蒸气喷出,此时在泄漏管壁周围会形成很小范围的冷点缺陷,笔者将冷点缺陷设置于管阵列中的不同位置,分析了管阵列发生泄漏时形成的冷点缺陷对声传播的影响.
过热器、再热器和省煤器的周期性排布构成典型的气-固型声子晶体.基于声子晶体理论,笔者以平面波展开法(PWE)为理论基础,采用Comsol有限元仿真对声波在管阵列传播形成的带隙结构进行研究[10-13].根据结果分析得出声源通过不同管阵列时的传播特性,以及冷点缺陷对传播特性的影响,为管阵列中声源定位和声波除灰声频的选择段提供理论依据,对锅炉声学理论的发展和其技术应用以及锅炉安全经济运行具有重要的意义.
1 理论模型
在数值计算中选用平面波展开法,获得声子晶体的带隙结构.同时选取不同结构进行计算,得到不同管阵列的声波带隙结构.在有限元仿真部分采用Comsol软件研究声波通过不同管阵列的透射特性以及存在冷点缺陷时的声传播特性.
1.1 数值计算模型
数值计算选取如图1所示的结构单元,其中A为空气基体,B为圆柱散射体,其半径为r,直径为d,结构单元x方向尺寸为a,y方向尺寸为b.在气-固型声子晶体中只需考虑纵波,其弹性波方程为:
(1)

根据布洛赫定理,式(1)的解为:
(2)
式中:K=(k1,k2)为平面内的二维布洛赫波矢;ω为平面波的角频率;G为二维晶格的倒格矢.

图1 二维声子晶体结构单元示意图
经过傅里叶变换,式(2)可以简化为标准特征方程:
(3)
其中矩阵D=P-1Q,而矩阵P和Q可以通过如下方程分别定义:
(4)
式中:δGG为Kronecker符号;F(G)为结构因子,通过求解上述方程的矩阵D得到其特征值,再求出其算术平方根,扫描整个不可约布里渊区,即可得到声子晶体的能带结构.
1.2 有限元模型
锅炉中不同结构的管阵列对声传播特性的影响不同,其声场分布也存在差异,通过研究不同管阵列的声传播特性可对炉内泄漏监测位置进行优化,从而增加声学监测精确度.炉内管阵列排布多以顺排结构存在,因此有限元仿真中采用正方形结构(即S型结构)与长方形结构(即R型结构)组合的结构单元,如图2所示.其中箭头表示声波入射方向,定义图2中正方形结构单元x方向尺寸为a1,y方向尺寸为b1;长方形结构单元x方向尺寸为a2,y方向尺寸为b2.

(a) ASR型结构

(b) MRS型结构
图2(a)中声波沿x正方向由管阵列左侧入射,右侧接收,声波先经过正方形结构,再经过长方形结构,2种结构交界面无错位,定义这种情况为ASR型结构.若声波沿x反方向入射,则定义为ARS型结构.
图2(b)中声波沿x反方向由管阵列右侧入射,左侧接收,声波先经过长方形结构,再经过正方形结构,2种结构交界面存在错位,定义这种情况为MRS型结构.若声波沿x正方向入射,则定义为MSR型结构.
管阵列中发生泄漏时,在泄漏管壁周围会形成很小范围的冷点缺陷,如图3所示,其中数字1~6为冷点缺陷所在位置,黑色的点为监测点.以泄漏在位置1为例,定义冷点缺陷为半径2r的同心圆,计算中设置环境温度为高温,在冷点缺陷位置设置低温参数,改变冷点缺陷位置.

图3 管阵列中存在冷点缺陷的仿真模型
2 计算与仿真结果分析
以省煤器为例,管阵列由外径d=(28~51) mm的无缝钢管构成,横向节距s1=(2~3)d,纵向节距s2≥(1.5~2)d.周期性管排结构中圆柱尺寸d=2r=40 mm,正方晶格尺寸a1=b1=2d=80 mm,长方晶格尺寸a2=160 mm,b2=80 mm或a2=80 mm,b2=160 mm.计算中所选用的材料参数见表1.

表1 计算中所用材料的参数
2.1 数值计算结果
正方晶格的数值计算结果如图4所示.波矢的方向代表声传播方向,其中Γ-X为0°方向的带隙结构.声波带隙频率Δω与声波带隙中心频率ωt的计算方法如下:
Δω=ωa-ωi
(5)
ωt=(ωa+ωi)/2
(6)
式中:ωa和ωi分别为带隙频率的上边界频率与下边界频率.

图4 正方晶格平面波展开法计算结果
由图4可知,声波不存在完全带隙,但存在方向带隙.正方晶格与长方晶格Γ-X方向的带隙结构对比如图5所示.

(a) a1=b1=80 mm

(b) a2=160 mm,b2=80 mm
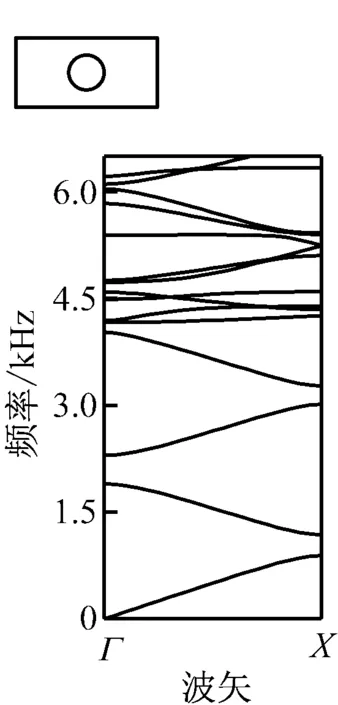
(c) a2=80 mm,b2=160 mm
由图5(a)可知,对于Γ-X方向的带隙结构,第一带隙频率为1 605.36~2 399.09 Hz,带隙宽度为793.73 Hz,带隙中心频率为2 002.23 Hz;第二带隙频率为3 750.26~3 975.80 Hz,带隙宽度为225.54 Hz,带隙中心频率为3 863.03 Hz.由图5(b)可知,第一带隙频率为1 844.76~1 892.45 Hz,带隙宽度为47.69 Hz,带隙中心频率为1 868.61 Hz;第二带隙频率为2 802.22~2 860.35 Hz,带隙宽度为58.13 Hz,带隙中心频率为2 831.29 Hz.由图5(c)可知,在Γ-X方向第一带隙频率为886.65~1 180.08 Hz,带隙宽度为293.43 Hz,带隙中心频率为1 033.37 Hz;第二带隙频率为1 892.45~2 298.60 Hz,带隙宽度为406.15 Hz,带隙中心频率为2 095.53 Hz.当声波连续通过2种不同结构时,不同晶格的声波带隙频率不同,其传播特性会发生变化,声波带隙频率也会增加或变宽.定义图5(a)与图5(b)组成的结构为1型结构,图5(a)与图5(c)组成的结构为2型结构.
2.2 仿真结果
根据之前的研究[3-4]可知,在某一方向当声波穿过管阵列数量N≥4时,其声波带隙频率基本不再发生变化.对于1型结构,选取正方形结构排数和长方形结构排数均为10;对于2型结构,选取正方形结构排数和长方形结构排数均为6.1型结构ASR型阵列记为1-ASR,以此类推.
2.2.1 声波入射不同管阵列的频谱特性
根据计算声波通过管阵列的声压级插入损失ΔS来描述声传播特性,其计算方法如下:
(7)
式中:S0为声源的声压级;S为声波通过管阵列后的声压级;p0为声源的声压;p为声波通过管阵列后的声压.
模拟中声源声压设置为1 Pa.1型结构的计算结果如图6所示,其中灰色区域表示声波单向导通的频率范围.图6(a)为不同晶格常数阵列交界位置的结构示意图.对比图6(b)与图6(c)可知,当声波先通过正方形结构,再通过长方形结构时(即对比1-ASR与1-MSR结果),2种晶格交界位置的放置对声传播特性影响很小,声波带隙频率基本保持不变.结合图5的计算结果,1型结构的长方晶格形成的声波带隙频率范围很小,可近似看成无明显带隙情况,并且第一带隙包含于正方形结构形成的带隙中.因此声波通过正方晶格后,形成的带隙结构不再发生明显变化,与之后的长方晶格与正方晶格放置位置关系不大.对于长方晶格第二带隙的消失,其原因是当声波通过正方晶格阵列后由于阵列的散射,其到达长方形结构阵列时不再是平面波入射.
对比1-ARS与1-MRS结果发现,长方晶格形成的第二带隙并未消失(图6中深灰色区域),但是其声传播规律发生了很大变化,即当声波先通过长方形结构阵列再通过正方形结构阵列时,2种结构交界面位置是否存在错位对声传播特性的影响很大.其形成原因与之前分析一致,声波通过长方形结构阵列时不再是平面波,交界面放置的形式不同,其声波入射到正方形结构阵列的方向也会发生相应变化,因此不同的放置情况对声传播特性会产生很大影响.并且由于声波先通过长方形结构阵列,由长方形结构阵列形成的带隙会优先存在,因此其形成的第二带隙不会消失.

(a) 管排结构

(b)1型顺排结构(c)1型错排结构
图6 声波通过不同管阵列的声压级插入损失
Fig.6 Insertion loss for sound passing through different tube arrays
对比图6中4种结构,1-ARS与1-ASR为同一种排布方式,声波入射的方向不同;1-MRS与1-MSR同样如此.由图6(b)和图6(c)还可知,声波通过2种不同的管阵列结构,当其排布方式相同时,不同的入射方向形成的声波带隙结构不同,并且某些频率存在声波的单向导通性即声二极管现象.图6(b)中频率为2 575~2 805 Hz时对于1-ARS为禁带,1-ASR为导带;频率4 775~5 015 Hz时对于1-ARS为导带,1-ASR为禁带.图6 (c)中对于1-MRS为禁带,1-MSR为导带的频段为2 495~ 2 605 Hz和2 665~2 865 Hz;对于1-MRS为导带,1-MSR为禁带的频段为1 650~1 795 Hz、2 225 ~2 395 Hz、4 875~5 150 Hz及5 245~5 400 Hz.锅炉中某一换热器管阵列存在多种管排结构时,声二极管现象对锅炉状态的声学监测会存在一定的影响,这是造成炉管泄漏漏报的原因之一.
根据声波单向导通频率,频率为4 940 Hz时的声波通过不同管阵列时的声压云图如图7所示.由图7(a)和图7(c)可知,通过长方形结构阵列入射到正方形结构阵列的声波不再是平面波,这与之前的分析一致.在长方晶格中,y方向两排圆柱之间的空气形成声波的主要通道.在接触面处不同的排布方式使声波在正方晶格以不同的状态传播:在图7(a)中声波分为2束通过正方形结构阵列;在图7(c)中声波由于接触边界位置的散射,声波先聚焦于正方晶格第6排位置,再以此位置为类点源辐射通过正方晶格.

(a)1-ARS(b)1-ASR(c)1-MRS(d)1-MSR
图7 频率为4 940 Hz时1型不同结构的声压云图
Fig.7 Sound pressure nephogram for various type 1 structures at 4 940 Hz
由图7(b)和图7(d)可知,虽然声波通过管阵列的能量很小,但接触面位置的反射仍对声压分布产生影响.在图7(b)中声波通过正方晶格后在长方形结构阵列中以沿圆柱之间的空气通道传播为主;在图7(d)中由于交界位置的错位排列,声波在边界位置类似于点源辐射到长方形结构阵列中.
2型结构的计算结果如图8所示,其中灰色区域表示单向导通的频率范围.对比图8(b)和图8(c)可知,2-ASR和2-MSR 2种晶格交界位置的放置对声传播特性影响很小,声波带隙频率基本保持不变;但是2-ARS与2-MRS的结果基本保持一致,这与图6(c)的结果存在很大差别,其原因在于2型结构中2种晶格的横向节距一致,声二极管现象减弱.

(a) 管排结构

(b)顺排结构(c)错排结构
图8 声波通过2型管阵列的声压级插入损失
Fig.8 Insertion loss for sound passing through type 2 tube arrays
图8中单向导通的频率范围均处在图5(c)结构产生的带隙位置.此处的带隙形成主要是由长方晶格引起的,灰色区域的第二与第三带隙均是声波先通过长方晶格再通过正方晶格的情况,这与图6的原因一致.灰色区域第一带隙是声波先通过正方晶格再通过长方晶格后形成的,与图6的结果存在差异.图6中以长方晶格为主要因素形成的带隙主要集中于较高的频率范围(高于2 500 Hz),而管阵列对高频声的散射影响要大于对低频声的散射.图8中长方晶格形成的第一带隙在低频范围(935~1 095 Hz),其管阵列对声波的散射影响很小,声波通过正方晶格(6排)后可看成是类平面波,其后的长方晶格仍可对此频段的声波产生影响.
2.2.2 冷点缺陷对声传播特性的影响
当换热器管阵列发生泄漏时,由于管道内外的压力差,处于其中的蒸气喷射出来会形成很小的低温区域,将此低温区域定义为冷点.在研究高温管阵列中存在冷态区域的情况时,管阵列所处温度设定为820 ℃,低温区域设定为120 ℃,冷点缺陷的位置参照图3.
图9给出了冷点缺陷位于管阵列中不同位置时的声传播特性,其中点线为无冷点缺陷时的声波带隙结构及传播特性曲线,深灰色区域表示由于冷点位置不同造成的声传播特性发生变化的频段.分析可知,当冷点处于不同位置时,声波带隙会发生微小变化,但声波带隙的总体趋势保持一致.当冷点位置与监测点不在同一直线上时,如位置5与位置6,冷点位置与监测点在y方向距离越大,对声波带隙的影响越小:如在位置5时,冷点位置与监测点在y方向相差1个晶格常数,在7 980~8 200 Hz范围内处于禁带,无冷点时此频段为导带,此时冷点对声传播特性产生影响;如在位置6时,冷点位置与监测点在y方向相差3个晶格常数,此时声传播特性与无冷点缺陷时的情况基本一致,冷点对声传播特性的影响很小.因此,在声传播方向的监测点与冷点位置在同一条直线上时,冷点对声传播特性才会有相对明显的作用,并且冷点在不同位置时对声传播特性的影响不同,此特点可为不同位置的冷点定位提供参考,进而对泄漏源的定位提供新的方法.

图9 冷点缺陷位于管阵列中不同位置时的声传播特性
在研究中发现冷点在不同位置时的声传播特性存在差异,其主要原因是声波在高温中的传播速度高于其在低温中的传播速度,声波在高温环境中传播遇到冷点时会发生声波的绕射现象,从而使管阵列声传播特性发生变化.基于此推测,选取8 000 Hz的声波在管阵列中传播,将冷点设定在位置1~位置6,其声压云图如图10所示.由图10可知,频率为8 000 Hz时,在声波通过冷点前位置产生声压增强点,通过冷点后位置产生声压减弱点,即声波通过冷点位置时发生绕射现象,这是由于在冷点位置的声传播速度小于周围环境的声传播速度引起的,并且冷点在不同位置对声传播特性会产生不同的影响.在图10(b)中冷点在位置1时与监测点相距6排管阵列,即相距监测点较远,声波在管阵列中由于其他管阵列的散射最终到达监测点时其声压云图与无冷点缺陷时基本一致.在图10(c)~图10(e)中由于冷点位置距监测点较近,声波通过管阵列后的声压云图发生明显变化,产生分束现象,其原因同样是由于声波绕射冷点以及管阵列对声波的散射作用.
冷点位置与监测点不在同一直线上的声压云图如图10(f)和图10(g)所示.在图10(f)中冷点位置偏离监测点较近,其声波绕射现象对监测点的声传播特性影响明显.在图10(g)中冷点位置偏离监测点较远,此时监测点的声压云图与无管阵列时相似.由图10还可知,对于8 000 Hz的声波,当冷点位置距离监测点较远时(图10(a)和图10(f)),监测点的声压云图不会发生明显的变化;冷点位置与监测点相距较近时,由于声波绕射原因对监测点的声压会产生较大的影响.
此种方法可归类于主动声学探测方法,在管阵列外施加声源,根据管阵列中不同位置的缺陷对声传播特性的影响,从而对缺陷位置进行定位.
3 结 论
(1) 声波通过不同管阵列结构,在某些频段存在声波的单向导通现象.
(2) 当横向节距不同,2种管阵列接触面位置存在错位时声波的单向导通现象明显,并且由于接触面的错位会产生声压汇聚现象.
(3) 当管阵列中存在冷点缺陷时会产生声波绕射现象,并且冷点在不同位置时,其声传播特性会发生不同变化.

(a)无冷点缺陷(b)位置1(c)位置2(d)位置3(e)位置4(f)位置5

(g)位置6
图10 频率为8 000 Hz,冷点在不同位置时的声压云图
Fig.10 Sound pressure nephogram for cold point at different locations of tube arrays at 8 000 Hz
(4) 当冷点位置距离监测点较远时,监测点的声压云图不会发生明显变化;当冷点位置与监测点相距较近时,对监测点的声压则会产生较大影响.
[1] ZHANG Shiping, SHEN Guoqing, AN Liansuo, et al. Power station boiler furnace water-cooling wall tube leak locating method based on acoustic theory[J].AppliedThermalEngineering, 2015, 77: 12-19.
[2] 王琳, 姜根山, 安连锁. 炉内管道泄漏声检测与定位系统的研究现状[J].应用声学, 2010, 29(1): 46-51.
WANG Lin, JIANG Genshan, AN Liansuo. Research status of the acoustic detection and location system for boiler tube leakage[J].AppliedAcoustics, 2010, 29(1): 46-51.
[3] AN Liansuo, WANG Peng, SARTI A, et al. Hyperbolic boiler tube leak location based on quaternary acoustic array[J].AppliedThermalEngineering, 2011, 31(16): 3428-3436.
[4] AFGAN N, COELHO P J, CARVALHO M G. Boiler tube leakage detection expert system[J].AppliedThermalEngineering, 1998, 18(5): 317-326.
[5] WIDARSSON B, DOTZAUER E. Bayesian network-based early-warning for leakage in recovery boilers[J].AppliedThermalEngineering, 2008, 28(7): 754-760.
[6] 姜根山, 刘月超, 安连锁. 基于声子晶体理论的炉内管阵列声透射特性数值研究[J].动力工程学报, 2014, 34(11): 850-855.
JIANG Genshan, LIU Yuechao, AN Liansuo. Numerical study on sound transmission through boiler tube arrays based on phononic crystal theory[J].JournalofChineseSocietyofPowerEngineering, 2014, 34(11): 850-855.
[7] 姜根山, 刘月超, 陈朵朵, 等. 基于声子晶体理论的管阵列声透射特性实验研究[J].动力工程学报, 2015, 35(3): 197-204.
JIANG Genshan, LIU Yuechao, CHEN Duoduo, et al. Experimental study on sound transmission across tube arrays based on phononic crystal theory[J].JournalofChineseSocietyofPowerEngineering, 2015, 35(3): 197-204.
[8] JIANG Genshan, LIU Yuechao, KONG Qian, et al. The sound transmission through tube arrays in power boilers based on phononic crystals theory[J].AppliedThermalEngineering, 2016, 99: 1133-1140.
[9] 刘月超. 电站锅炉内换热器管阵列的声传播特性[D]. 保定: 华北电力大学, 2014.
[10] 齐共金, 杨盛良, 白书欣, 等. 基于平面波算法的二维声子晶体带结构的研究[J].物理学报, 2003, 52(3): 668-671.
QI Gongjin, YANG Shengliang, BAI Shuxin, et al. A study of the band structure in two-dimensional phononic crystals based on plane-wave algorithm[J].ActaPhysicaSinica, 2003, 52(3): 668-671.
[11] CAO Yongjun, HOU Zhilin, LIU Youyan. Finite difference time domain method for band-structure calculations of two-dimensional phononic crystals[J].SolidStateCommunications, 2004, 132(8): 539-543.
[12] KUSHWAHA M S, HALEVI P, DOBRZYNSKI L, et al. Acoustic band structure of periodic elastic composites[J].PhysicalReviewLetters, 1993, 71(13): 2022-2025.
[13] 姜根山, 张荣英, 安连锁, 等. 周期性管阵列的声传播特性实验研究[J].中国电机工程学报, 2011, 31(29): 9-14.
JIANG Genshan, ZHANG Rongying, AN Liansuo, et al. Experimental study on the propagation characteristics of sound wave through periodic tube arrays[J].ProceedingsoftheCSEE, 2011, 31(29): 9-14.
——居住在“冷点社区”与健康欠佳、享有卫生服务质量欠佳间的关系

