带煤质校正的循环流化床锅炉新型协调控制方法

何 鹏， 陆琳辉， 刘西陲， 李益国

(1．安徽电气工程职业技术学院，合肥 230051；2．国网安徽省电力公司培训中心，合肥 230022；3．东南大学 能源与环境学院，南京 210096)

与传统的煤粉炉相比，循环流化床锅炉(CFBB)具有燃烧效率高、燃料适应性广、燃烧污染低、脱硫效率高和投资成本低等优点.但由于其具有多变量、强耦合和大迟延等特性，CFBB的协调控制一直以来都是研究的热点与难点.

目前，CFBB的协调控制主要采用常规PID加前馈解耦的设计方法[1-3]，但由于其具有大迟延特性，以及动态解耦很难实现，常规的控制方法很难取得理想的调节效果.近年来也有学者基于神经网络或自抗扰控制等先进控制理论对该问题开展研究工作[4-7]，但这些算法要么过于复杂，要么参数整定困难，不利于工程应用.CFBB协调控制普遍还存在以下问题：(1)仍延用与常规煤粉炉相同的控制结构，无法充分利用炉膛蓄热加快负荷响应速率；(2)在设计先进控制方案时很少同时考虑煤质校正问题.而煤质变化意味着协调控制对象的特性发生了变化，如果不对控制器进行相应调整，显然会严重影响控制品质.

笔者提出一种具有煤质校正功能的CFBB新型协调控制方法.该方法将一次风量引入协调控制中作为新的控制量，以充分利用床料中的未燃尽碳和炉膛蓄热量，提高负荷跟踪能力，相应增加炉膛床温作为输出量，保证燃烧安全与脱硫脱硝效率.同时采用基于扩增状态空间模型的多变量预测控制算法，应对CFBB的大迟延和强耦合特性，最后基于扰动观测器设计了煤质在线校正环节，提高了控制系统适应煤质变化的能力.

1 基于扩增状态空间模型预测控制的CFBB新型协调控制方法

1.1 新型协调控制结构

CFBB协调控制一般采用与普通煤粉炉一致的控制结构，即以给煤量指令和汽轮机调门指令为输入量，机组功率和主汽压力为输出量(见图1).

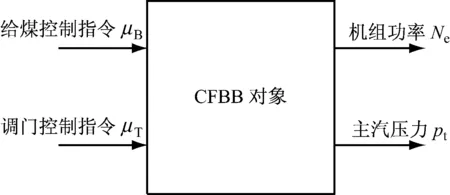
图1 传统CFBB协调控制方法结构图

然而由于CFBB的迟延特性远大于传统的煤粉炉，且一般仍采用PID控制器加前馈解耦的控制策略，该方案的负荷响应速率很难满足自动发电控制(AGC)的要求，应用效果不佳.

笔者把一次风量引入CFBB协调控制中作为新的控制量，以充分利用床料中的未燃尽碳和炉膛蓄热，提高变负荷初期的负荷响应速率，同时把床温引入协调控制中作为新的被控参数.为了提高稳定性，减少控制器的频繁动作，炉膛床温控制采取区间控制的方案，即不针对炉膛床温设置具体的特定设定值，只需要满足炉膛床温在850～950 ℃内变化即可.针对CFBB的大迟延和强耦合特性，采用基于扩增状态空间模型的多变量预测控制算法设计控制器，最终得到CFBB新型协调控制结构，如图2所示.图中Tb为炉膛床温，μW为一次风调门指令，Ne,r和pt,r分别为机组功率、主汽压力的设定值.

图2 CFBB新型协调控制结构图

Fig.2 Structure of the new coordination control method for CFBB

此外，新型协调控制结构中引入的一次风除了直接影响炉膛床温之外，还会对炉膛床压产生干扰，而炉膛床压的稳定对CBBB的安全运行同样至关重要.目前针对CFBB炉膛床压的控制方案已经比较成熟，可通过解耦由传统单回路PI控制实现，这部分内容并不是本文研究的重点，故不再对此环节进行深入研究.

1.2 基于扩增状态空间模型预测控制的CFBB协调控制方法

采用基于扩增状态空间模型的多变量预测控制算法设计控制器，该算法能够很好地应对CFBB的大迟延和多变量强耦合特性，并具有更好地抑制不可测扰动的能力.

1.2.1 预测控制算法

设CFBB协调控制对象可以用式(1)所示的状态空间模型来描述：

(1)

为消除建模误差和不可测扰动的影响，将内扰项d(k)作为扩增状态量对原状态变量进行扩充，得到扩增状态空间模型：

(2)

其中，

(3)

(4)

(5)

(6)

(7)

式中：I为单位矩阵;d1(k)、d2(k)和d3(k)分别为3个主回路的内扰.

(1) 输出预测.

预测模型可表示为

Y(k)=FX(k)+ΦU(k)

(8)

其中，

(9)

(10)

(11)

(12)

式中：P、M分别为预测控制算法的预测时域和控制时域；U(k)为从k时刻起未来M步的控制量；Y(k)为基于k时刻的未来P个时刻的预测输出量.

(2) 滚动优化.

首先基于式(13)计算稳态控制量us(k)和稳态状态量Xs(k)：

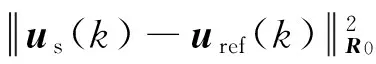
(13)

式中：Js(k)为性能指标函数；uref为设定值w(k)对应的稳态参考控制量；R0为控制权矩阵.

(14)

(15)

(16)

(17)

式中：r1、r2和r3分别为给煤量指令、汽轮机调门指令和一次风调门指令对应的控制权系数；μB,s(k)、μT,s(k)和μW,s(k)分别为给煤量指令、汽轮机调门指令和一次风调门指令的稳态值；μB,ref(k)、μT,ref(k)和μW,ref(k)分别为给煤量指令、汽轮机调门指令和一次风调门指令的稳态参考值.

再基于us(k)构造控制量目标值Ur(k)，即

(18)

基于时刻k制定性能指标J(k)来计算最优控制量：

(19)

其中，ω(k)为输出设定值.

(20)

(21)

矩阵Q和R分别为误差权矩阵和控制权矩阵，且

(22)

(23)

式中：q1和q2分别为机组功率和主汽压力对应的误差权系数.

预测控制算法性能指标的约束条件为

(24)

式中：i=0,1,…,M-1;j=1,…,P；dμB、dμT、dμW为控制量的增量；下标min、max分别表示最小值和最大值.

从式(21)～式(24)可以看出，不同于传统的多变量预测控制算法，为实现炉膛床温变量的区间控制，在构造控制算法的性能指标时，不具体考虑炉膛床温参数的设定值，而是将其作为约束加入到约束条件中.而炉膛床温Tb可以通过预测控制算法的预测模型(式(8))计算获得，所以关于炉膛床温的约束实际上依然是对于控制量μB、μT和μW的约束.

结合性能指标函数和约束条件，计算当前时刻最优相对控制量Δu(k)，当前时刻的控制量u(k)则可表示为

u(k)=us(k)+Δu(k)

(25)

1.2.2 状态估计

由于状态量无法直接测量，利用扩增状态卡尔曼滤波器对状态量进行估计.MIMO对象离散时间线性时不变系统的状态空间描述如下：

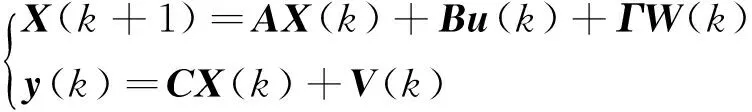
(26)

式中：V(k)为输出侧的测量噪声；W(k)为过程噪声；Γ为系统噪声输入矩阵，一般可取单位阵.

(27)

其中，V1(k)、V2(k)和V3(k)分别为3个输出量的测量噪声；W1(k)、W2(k)和W3(k)分别为过程噪声.认为测量噪声V(k)和过程噪声W(k)均为白噪声，且两者互不相关.状态估计时不涉及炉膛床温的控制问题，因此这里的计算都是基于完整的3×3模型进行的.

状态量可通过下式进行估算：

(28)

式中：L0为滤波器增益向量.

未来时刻的扩增状态量可由式(29)计算获得：

(29)

联立式(28)和式(29)可得滤波器状态估算表达式：

(30)

L=AL0

(31)

预测增益向量L可由下式计算获得：

(32)

式中：Rn为测量噪声V(k)的方差矩阵；P为误差协方差矩阵，可由离散Riccati方程计算获得.

(33)

式中：Qn为过程噪声W(k)的方差矩阵.

2 基于扰动观测器的煤质校正技术

CFBB主要燃烧劣质煤，煤质多变，而煤质变化意味着协调控制对象的特性，尤其是增益发生变化，如果不对控制器作相应调整，必将严重影响协调控制系统的品质.为此，笔者进一步提出了基于扰动观测器的煤质在线校正方案.

2.1 扰动观测器

图3 常规扰动观测器结构框图

2.2 带煤质校正环节的多变量预测控制

所提出的带煤质校正的CFBB协调控制结构图见图4.图中，GBN(s)、GUN(s)、GWN(s)、GBP(s)、GUP(s)、GWP(s)、GBT(s)、GUT(s)和GWT(s)分别为协调控制系统的9个子控制对象.假设煤质变化仅对给煤通道的传递函数产生影响，即煤质发生变化时，仅GBN(s)、GBP(s)和GBT(s)模型发生变化，且认为仅对函数的稳态增益产生影响，不考虑时间常数T和时滞常数τ的变化.

图4 带煤质校正的多变量预测控制结构

Fig.4 Structure of a multivariable predictive controller based on coal-quality correction

给煤量-机组功率、给煤量-主汽压力和给煤量-炉膛床温通道的煤质校正原理相同，为简单起见，下面仅以给煤量-机组功率通道为例说明设计过程.煤质扰动主要影响传递函数GBN(s)的稳态增益，因此提出基于扰动观测器的煤质校正方案(见图5).

图5 基于扰动观测器的煤质校正环节

图5在原扰动观测器的基础上添加了积分环节和死区环节.由图5可知，煤质发生变化时，对象的增益相应发生变化，原始模型GBN(s)与标称模型G(s)出现偏差而产生偏差值Δ，积分环节对该偏差值进行累积来校正标称模型G(s)的增益，当校正后的标称模型G(s)′与煤质变化后的模型GBN(s)′的增益一致时，偏差就可以被消除，随后煤质校正环节也就停止工作，因此积分环节可以用于估算煤质变化造成的稳态增益变化值.同时，利用该估算值对预测控制算法的预测模型进行修正，从而降低煤质变化对控制回路造成的影响，提高系统的抗扰动能力；此外，为防止过小的偏差引起控制器的频繁动作，提高系统整体的稳定性，在煤质校正方案中相应增加了死区环节.

3 仿真研究

3.1 仿真对象

基于某电厂330 MW CFBB某负荷工作点的动态实验数据，通过Matlab软件辨识以及数据验证，得到基于新型协调控制结构的3×3 CFBB控制对象传递函数模型GCFB(s)：

(34)

本文的仿真研究主要侧重于预测对控制算法与煤质校正环节的验证，而CFBB模型本身的非线性特性研究不在本文讨论范围内，因此可将CFBB模型简化为线性模型，由式(34)所示的传递函数模型表示.基于上述假设，认为该模型在特定工况点的仿真结果可直接推广到其他工况点，故在下文的仿真验证中，仅以某一稳定工作点为例予以说明.

3.2 基于扩增状态空间模型的新型协调控制方法的仿真分析

分别对扩增状态量的预测控制算法和常规PID控制算法的控制效果进行比较分析.

(1) 预测控制参数.

采样时间Ts=20 s，预测时域P=100，控制时域M=20，误差权系数q1、q2均取2，控制权系数r1、r2和r3分别取80、30和20.

(2) PID参数.

采用实际微分环节来代替原始定义中的微分环节，故该模块共有4个参数：P、I、D和N.

利用PID模块的自整定功能对上述被控对象的控制器参数进行多次整定，可得：

PID1P=0.2,I=0.000 8,D=0.001,N=100

PID2P=-0.2,I=-0.003,D=4,N=100

PID3P=-0.01,I=-0.000 5,D=3,N=100

其中，PID1、PID2和PID3分别为μB→Ne，μT→pt和μW→Tb主回路的控制器.

在某稳态工作点Ne=300 MW，pt=16 MPa，Tb=850 ℃开始进行仿真试验.目前火电机组实际负荷响应速率一般要求大于1.5%Pe/min(Pe表示额定负荷)[1]，为说明预测控制算法的实际效果，此处假定机组功率的设定值以5.0%Pe/min的升负荷速率(即16.5 MW/min)，由300 MW斜坡升至320 MW，主汽压力pt设定值维持不变，炉膛床温Tb维持在850～950 ℃.仿真结果见图6.

(a) 控制量示意图

(b) 控制效果示意图

图6 预测控制算法效果对比

Fig.6 Comparison of control effectiveness between two algorithms

由图6可知，整体上预测控制算法凭借滚动优化和反馈校正等环节积累的优势，负荷跟踪较快，过渡时间较短，控制效果优于常规PID控制，控制量也未发生剧烈波动，炉膛床温可以保证在合理的变化范围内；而常规PID控制效果不甚理想，不仅负荷跟踪滞后明显，主汽压力的控制效果在设定值稳定后仍然不理想.同时，当炉膛床温控制设置为区间控制时，由于PID3模块基于μW→Tb主回路的误差，当炉膛床温在850～950 ℃时，PID3模块不能发挥作用，即控制量保持不变，此时对象的控制效果完全依赖于μB、μT；而在预测控制中，即使炉膛床温值处于合理范围内，预测控制算法依然可以通过μW来提高Ne和pt的跟踪能力，优化整体控制效果，预测控制的优化效果更显著.

以上仿真结果验证了预测控制算法在处理多变量、强耦合、大延迟对象时的突出优势，同时也说明了新型协调控制结构的合理性.

3.3 带煤质校正环节的预测控制算法仿真

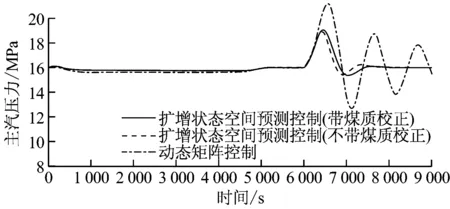
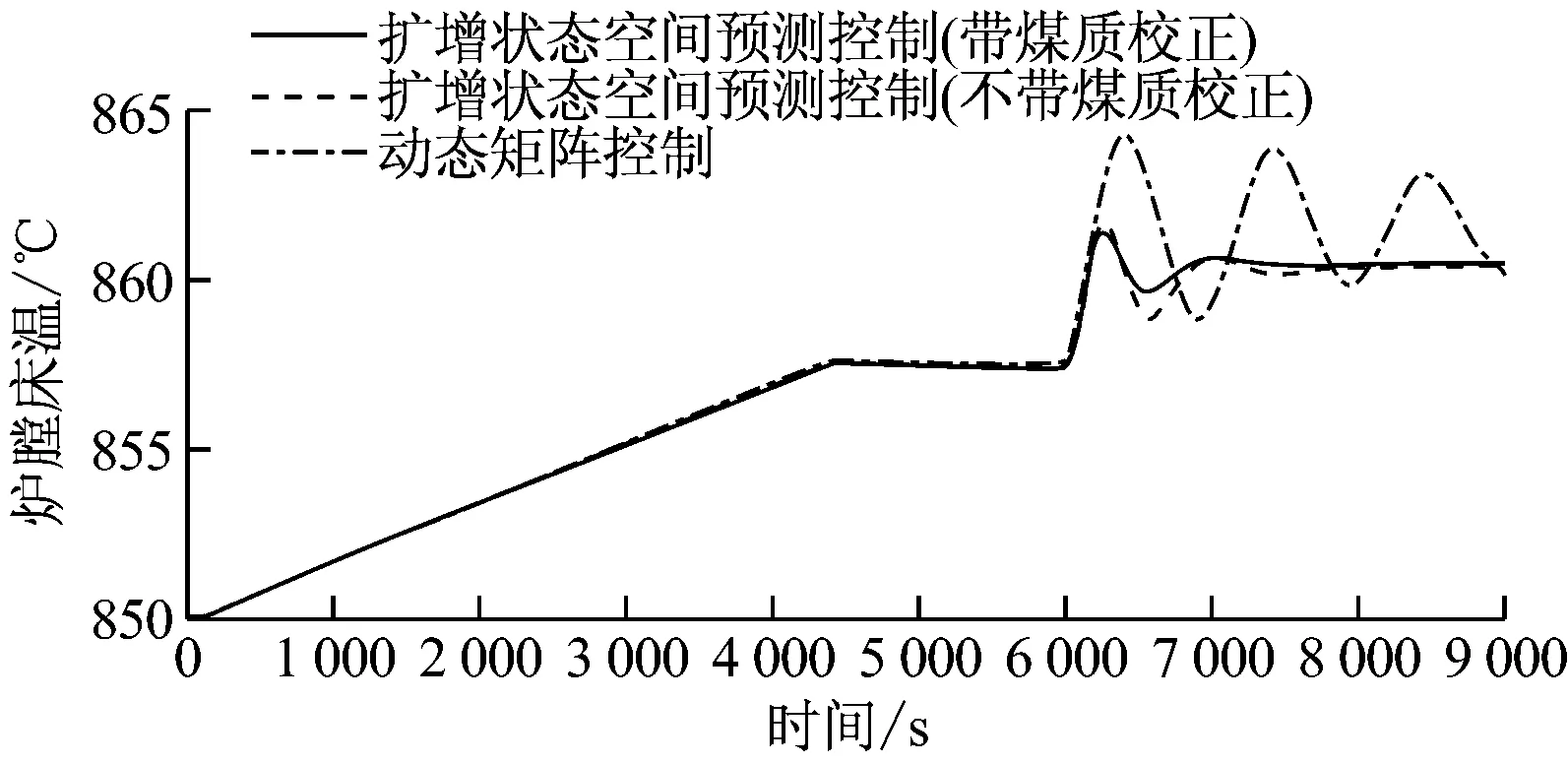
对该330 MW CFBB采用扩增状态空间模型多变量预测控制算法进行分析.在6 000 s时，分别对GBN(s)、GBP(s)和GBT(s)的稳态增益乘以常数1.5、1.6和1.7，用来模拟此时由于煤质变化造成的模型变化，其扰动抑制效果如图7所示.从图7可以看出，对于扩增状态空间模型多变量预测控制算法与常规动态矩阵控制(DMC)算法而言，两者在煤质未发生变化时的控制效果相仿；对于带煤质校正环节和不带煤质校正环节的扩增状态空间模型多变量预测控制算法而言，若煤质不发生明显变化，煤质校正环节不工作，两者的控制曲线完全一致；当煤质发生明显变化时，煤质校正环节可以较好地消除该扰动的影响，输出量波动明显减小，且可以较快跟踪上设定值，提高快速性和稳定性，相应控制量波动有所减小，可以较快稳定下来.不带煤质校正环节的预测控制算法由于预测模型失配，控制量和输出量均呈现明显波动，由于扩增状态空间模型多变量预测控制算法本身的抗扰动能力也有所改善，故输出量和控制量仍可较快稳定下来，但带煤质校正环节的控制结构整体扰动抑制效果要更为理想.相比而言，常规DMC算法在预测模型发生失配时，控制量和被控量均出现明显的波动，且被控量超调量较大，稳定性变差，控制品质趋于恶劣.

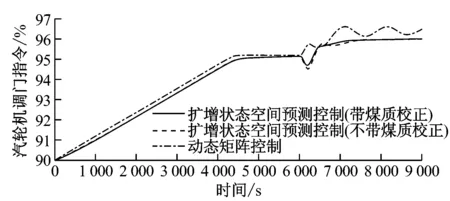
(a) 控制量示意图

(b) 控制效果示意图

图7 煤质校正效果对比

Fig.7 Comparison of coal-quality correction effectiveness

图8给出了煤质校正环节对于煤质变化系数的估算值.从图8可以看出，煤质校正环节能够很好地估算出煤质变化系数，其准确性和快速性都较为理想.

图8 煤质变化系数估算值

4 结 语

由于CFBB具有大延迟、大惯性、强耦合等显著特点，同时其煤质变化也较为频繁，故提出了一种新型协调控制结构，在原2×2协调控制结构的基础上引入一次风量作为控制量并相应增加炉膛床温参数作为输出量，从而构成3×3控制结构，此外针对煤质变化提出了基于扰动观测器的煤质校正方案.仿真结果表明，该新型控制方法的负荷跟踪速率快，过渡时间短，控制效果明显优于常规PID控制，同时煤质校正环节可以较好地消除煤种变化带来的影响，被控参数的波动明显减小.

[1] 杨佳梁. 300 MW循环流化床协调控制系统的研究与应用[D]. 北京: 华北电力大学, 2013.

[2] 赵永刚, 朱永红. 协调控制在135 MW循环流化床锅炉的应用[J].自动化技术与应用, 2013, 32(7): 111-116, 119.

ZHAO Yonggang, ZHU Yonghong. Coordinated control in 135 MW CFB boiler[J].TechniquesofAutomationandApplications, 2013, 32(7): 111-116, 119.

[3] 吴玉平, 王永龙. 机跟炉协调控制在300 MW CFB锅炉煤质大幅波动时的应用[J].中国电力, 2008, 41(12): 42-45.

WU Yulong, WANG Yonglong. Application of turbine following boiler coordinated control in 300 MW CFB boiler against the great change in coal quality[J].ElectricPower, 2008, 41(12): 42-45.

[4] 郑佳亮. 基于自抗扰控制的300 MW循环流化床机组负荷协调控制系统的研究[D].太原：山西大学,2013.

[5] 曾祥平. 循环流化床锅炉负荷协调控制系统研究[D].厦门：厦门大学,2007.

[6] 赵东梅. 300 MW循环流化床锅炉协调控制系统[D]. 北京：华北电力大学,2008.

[7] 黎倩.模糊鲁棒控制在循环流化床锅炉控制中的应用研究[D].石家庄：河北科技大学，2010.

[8] CHEN X S，YANG J，LI S H，et al．Disturbance observer based multivarible control of ball mill grinding circuits [J]．JournalofProcessControl，2009，19: 1205-1213．