丢番图方程x3+27=67y2整数解的研究

李双娥，李光华，上官军胜，林春华，王勇红

(江西师范高等专科学校，江西 鹰潭 335000)

对于丢番图方程x3±27=Dy2(D>0)，当D没有6k+1的素数的奇次方因数时，其解的结构已由曹玉书[1]得到.但当D有6k+1形状的素因数时，它的整数解较难求出.本文利用递归数列、同余式和平方剩余研究了丢番图方程x3+27=67y2的整数解，得到它的全部整数解为(x,y)=(-3,0),(1320,5859).

引理[2]丢番图方程x3+1=201y2的全部整数解为(x,y)=(-1,0)，(440,±651).

定理丢番图方程

x3+27=67y2

(1)

的全部整数解为(x,y)=(-3,0)，(1320,±5859).

当x不是3的倍数时，方程(1)化为(x+3)(x2-3x+9)=67y2，因为(x+3,x2-3x+9)=1，故丢番图方程(1)可以转化为以下两种情况：

情况Ⅰx+3=67u2x2-3x+9=v2，y=uv；

情况Ⅱx+3=u2，x2-3x+9=67v2，y=uv.

下面讨论这两种情况的(1)的整数解：

情况Ⅰx2-3x+9=v2可化为(2x-3)2-(2v)2=-27，此时x=-5,8,0,3均不满足x+3=67u2，故此时没有丢番图方程(1)的整数解.

情况Ⅱx2-3x+9=67v2可化为(2x-3)2-67(2v)2=-27.因为方程x2-67y2=-27的全部整数解，由以下4个非结合类给出[3]：

(2)

(3)

(4)

(5)

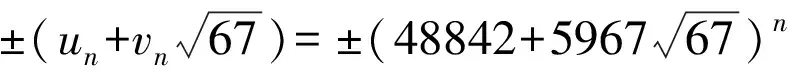
2u2=xn+9

(6)

(7)

(8)

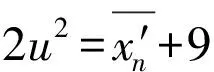
(9)

(10)

(11)

对于(6)，由(10)可得：

xn+2=97684xn+1-xn，x0=311，x1=30381844

(12)

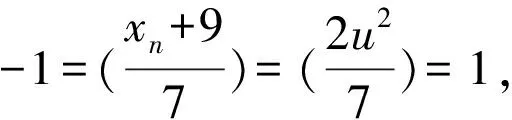
下面再来讨论(7),由(11)易得递归关系：

(13)

综上所述，丢番图方程(1)的全部整数解为(x,y)=(-3,0)，(1320,±5859).

[1] 曹玉书.关于丢番图方程x3±27=Dy2[J].黑龙江大学自然科学学报,1988(2):4-8.

[2] 李双志,罗明.关于不定方程方程x3+1=201y2[J].西南师范大学学报(自然科学版),2010(1):11-14.

[3] 柯召,孙琦.谈谈不定方程[M].上海:上海教育出版社,1980.