高速列车作用下铁路隧道内轨枕受力的理论解析及验证

王志伟，马伟斌，杜晓燕

(中国铁道科学研究院 铁道建筑研究所，北京 100081)

高速铁路因其效率高、经济效益好等显著优点已经在全世界范围内迅速发展[1]。高速运行时轨枕受力对刚度较大的板式无砟轨道板振动冲击强度相应提高。目前国内外对接触反力的研究较多。现场实测方面，彭立敏等[2]以蜈蚣岭隧道为现场试验工点，测试了隧道底部结构竖向动应力及竖向加速度在仰拱的分布情况，但仅限于特定隧道。数值分析方面，张玉娥等[3]确定了2种列车接触反力的定量分析方法，并采用有限元软件对隧道底部结构以及围岩进行了动力分析，得到不同车速条件下隧道底部结构的动力响应特征。由于采用“列车-轨道-隧道”一体化模型，该方法能很好地反映列车荷载的时间和空间效应，但是因理论求解时过于复杂，应用在数值计算中较困难。理论分析方面，梁波等[4]从引起车辆振动的几何不平顺入手，采用英国轨道不平顺管理标准值对应的激振力推导了列车轨枕受力，通过非线性数值分析，揭示了路基不同部位刚度变化对基面变形、动应力及加速度的影响规律。然而轮轨接触反力与钢轨的强度、刚度及列车本身的振动密切相关，由于推导过程中假设钢轨为刚性结构，故计算结果偏大。此外，其研究结果尚不能反映列车荷载的移动特性与车厢前后2个转向架对于同一点轨枕受力的叠加效应，因而误差较大。

本文通过理论分析和数值计算，分析隧道底部结构特定监测点的竖向应力及竖向加速度的动力响应特征。

1 半无限空间连续体任一点的时频域动力响应函数

列车行进时，轨道上作用一个随时间变化的列车荷载p(t)，其与时间相关，为一时频响应函数，又由于列车荷载沿着钢轨方向推进，故p(t)为时频域响应函数。假设铁路钢轨为半无限空间连续体，轨道上一点x0竖向动力响应可由广义Duhamel公式表示。

(1)

式中:μz(x0,t)为t时刻x0处在p(t)作用下产生的竖向位移响应函数；hzz(x0,y,t-τ)为y=0处作用竖向单位脉冲荷载时在x0处的竖向位移响应；p(τ)为t=τ时列车荷载函数。

因为t<τ时，hzz(x0,y,t-τ)=0，则式(1)可变化为

(2)

假设在某一时刻τ，列车荷载从原点处以速度v沿y轴正向移动到y0=vτ处，则式(2)可变化为

(3)

因铁路钢轨刚度很大，在列车作用下可认为其始终处于线弹性状态。根据动力互等原理得

hzz(x0,vτ,t-τ)=hzz(vτ,x0,t-τ)

(4)

则式(3)可变化为

(5)

由式(1)和式(5)可知，当列车荷载作用在y0=vτ处对x0处的动力响应等于在x0处作用列车荷载时y0=vτ处的动力响应。由轨距与列车车轮直径的关系可知，2个轨枕之间只可能作用一对列车轮载，若只研究在动力作用点处的动力响应，则有t=τ0。此时式(5)可进一步简化为

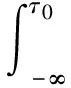
(6)

2 高速列车荷载作用下温克尔弹性梁方程解

如图1所示，当钢轨上作用单位脉冲荷载时，p(t)=1。此时根据竖向受力平衡有

(7)

式中：E为钢轨的弹性模量；I为钢轨惯性矩；x为任一点的横坐标；μ(x)为钢轨的挠度；ρ为钢轨的密度；A为钢轨的横截面积；q为基础分布反力。

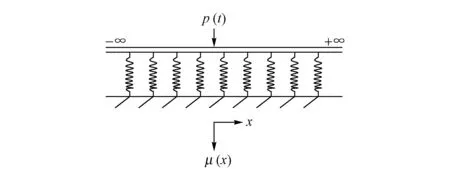
图1 钢轨连续梁模型

在数值计算过程中忽略钢轨的重度，则式(7)可简化为

(8)

根据温克尔假定：q=E′μ(x),上式可变化为

(9)

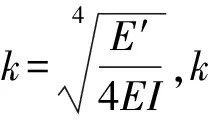
解方程(9)可得

μ(x)=c1ekxcoskx+c2ekxsinkx+

c3e-kxcoskx+c4e-kxsinkx

(10)

根据边界条件，在无穷远处钢轨的竖向挠度为0，竖向振动速度也为0，即

(11)

(12)

综合式(11)和式(12)，可得

(13)

(14)

3 轨枕受力解析式

为求解任意时刻轨枕受力表达式，引入英国铁路技术中心推荐的轨枕受力计算公式。该公式为

(15)

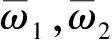
(3) 三种因素都会对排水管的淤塞造成影响，随着水力梯度、排水管壁面积以及土体黏粒含量的增大，排水管的淤塞会有不同程度上的加剧。

英国轨道几何不平顺管理值见表1。

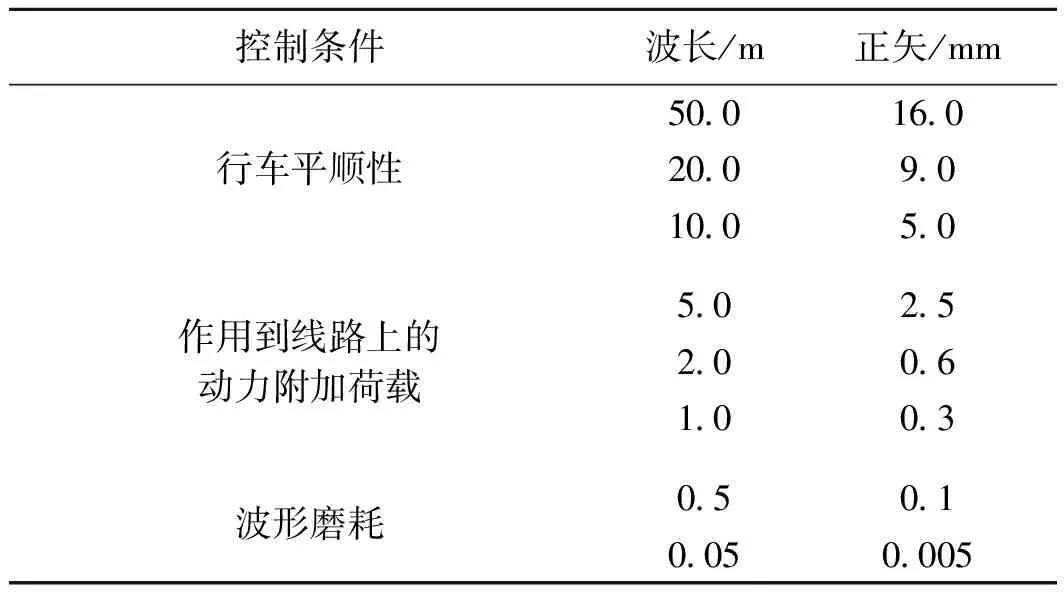
表1 英国轨道几何不平顺管理值

令列车的簧下质量为m，则相应的振动荷载幅值为

(16)

由式(6)和式(14)可得

(17)

根据温克尔假定，且轨枕受力R近似等于基础分布反力q与轨枕间距a的乘积，得列车作用下轨枕受力R=qa=E′aμz(x0,t)，将式(15)和式(17)代入得

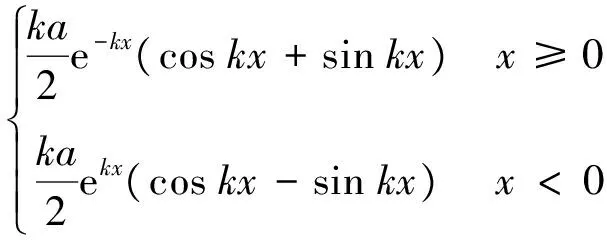
(18)

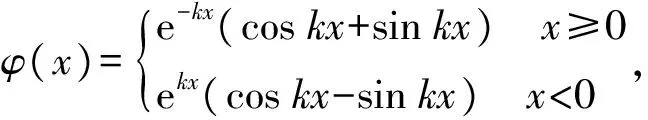
(19)

传递系数φ(x)随变量kx的变化曲线见图2。可见，传递系数最大值为1，随kx变化传递系数呈两头小中间大的趋势。

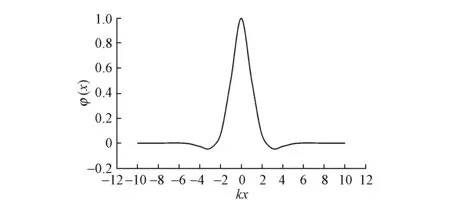
图2 传递系数φ(x)随变量kx的变化曲线

图3 列车模型示意

综上，轨枕受力的最终表达式为

(20)

4 工程案例分析

4.1 模型的建立

杜明庆等[10]通过现场实测分析了兰新二线福川隧道基底动力响应规律。本文以该隧道为例进行对比分析，设计断面见图4。隧道埋深190 m，宽14.7 m，高12.23 m；仰拱厚0.55 m，填充层厚1.25 m；道床板宽2.80 m，高0.29 m。

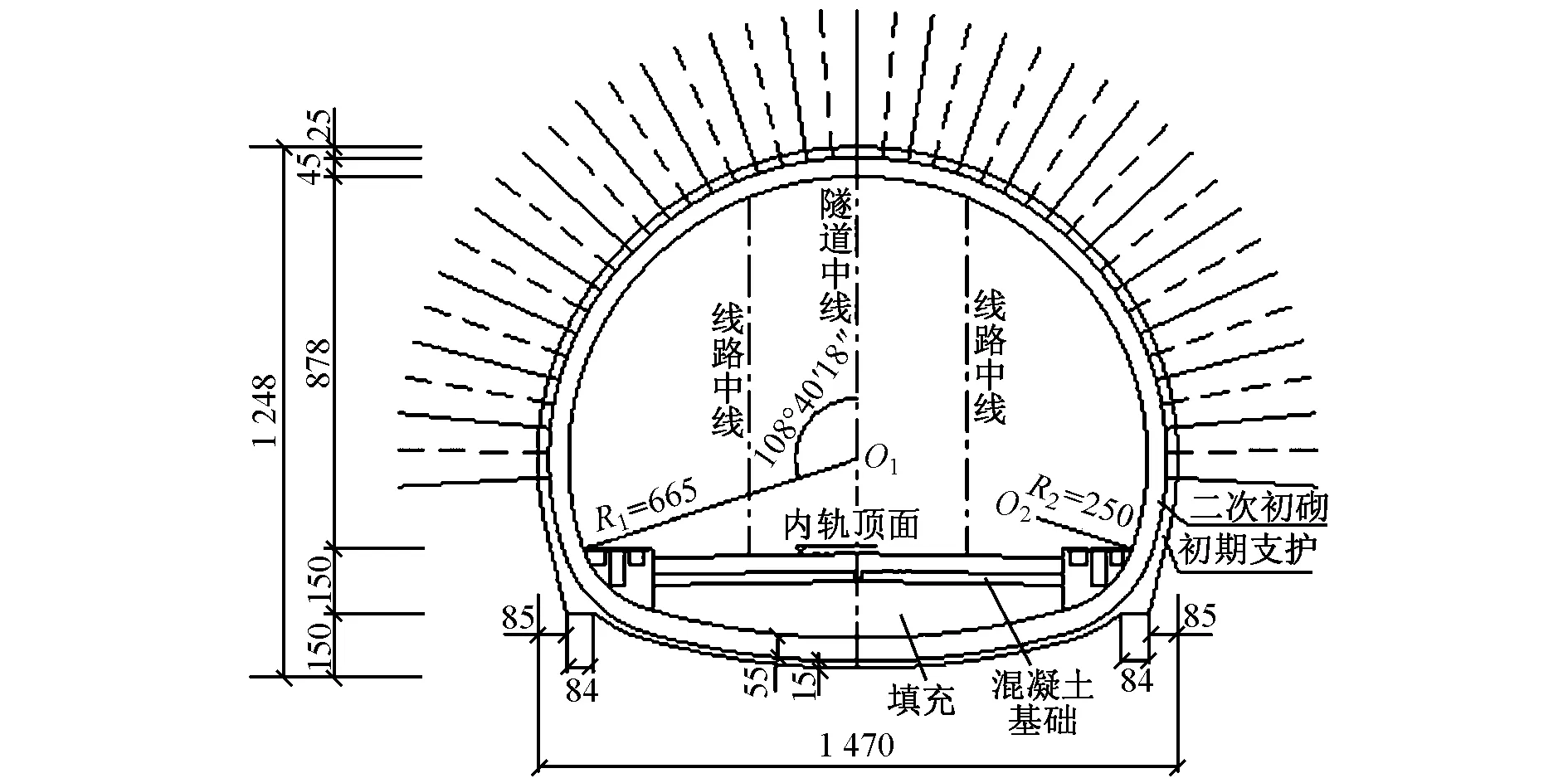
图4 隧道设计断面(单位：cm)

采用有限差分软件FLAC 3D建立数值模型(见图5)，模型长120 m，宽60 m，厚1 m。动力计算之前的应力状态对基底结构的动力响应有很大影响，因此在进行动力计算之前进行地应力初始平衡和隧道开挖计算，然后在此基础上进行动力响应分析。

图5 数值模型

4.2 边界条件与计算参数

初始平衡以及隧道开挖计算过程中采用固定边界条件，动力计算过程中采用黏性动力边界，以消除边界上动力波的反射误差。

计算过程中围岩采用Mohr-Coulomb本构模型，衬砌、水沟、填充层和道床板采用D-P本构模型。围岩以及隧道结构的物理力学参数分别见表2与表3。动力计算过程中采用瑞利阻尼。监测点的布置见图6。

表2 围岩物理力学参数

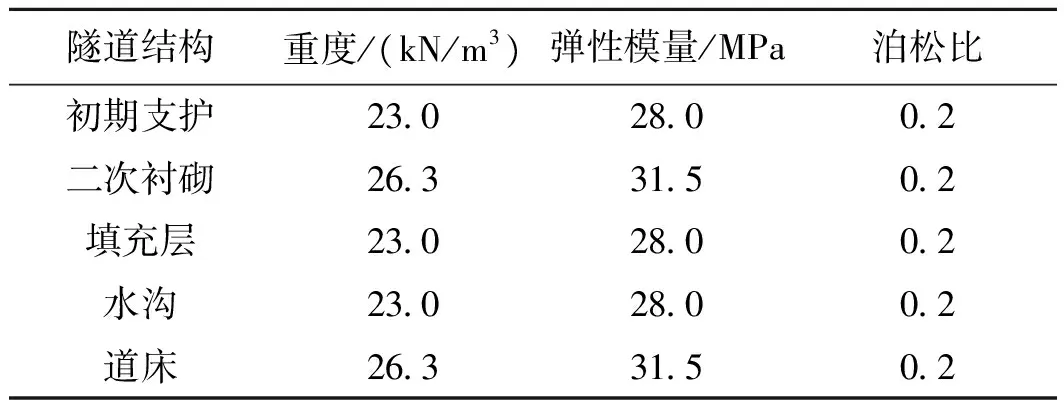
表3 隧道结构物理力学参数

图6 监测点布置(单位：mm)

4.3 结果分析

4.3.1 不同行车速度下测点的竖向动应力响应

图7 200 km/h时测点2竖向动应力时程曲线

实测时列车通过隧道采取减速措施。行车速度取50,100，200 km/h。200 km/h时测点2竖向动应力时程曲线见图7。可知，当轮对未对底部结构造成影响时，监测点竖向动应力基本保持不变，随着轮对接近，监测点动应力响应变化显著。由于1节车厢有2个转向架4个车轮，因此动应力时程曲线出现了2个动应力峰值区域。由于2个轮对的距离很近，因此对轨枕受力的影响有交叠的作用，竖向动应力的最大值也出现在轮对作用在测点时。

不同行车速度下测点竖向动应力随距填充层顶面距离变化曲线见图8。可知，模拟值与实测值的变化规律基本相同。行车速度为100 km/h时由测点1到测点2竖向动应力实测值衰减率为20%，模拟值衰减率为19.5%。在其他各测点之间实测值和模拟值衰减率也近似相等。实测值与模拟值接近，可证明轨枕受力数学表达式的正确性。

图8 不同行车速度下测点竖向动应力随距填充层顶面距离变化曲线

4.3.2 不同行车速度下测点竖向加速度响应

行车速度200 km/h时测点2竖向加速度时程曲线见图9。可见曲线明显分成了2个峰值区域，说明2节车厢转向架处的轮对对基底结构的作用更加显著。

图9 200 km/h时测点2竖向加速度时程曲线

图10 不同行车速度下测点竖向加速度随距填充层顶面距离变化曲线

不同行车速度下测点竖向加速度随距填充层顶面距离变化曲线见图10。可知：①模似值比实测值略大，但是变化规律基本一致，并且竖向加速度的衰减规律和竖向动应力基本一致。②相同速度下大部分测点实测值与模拟值的相对差值也保持在20%以内。速度为50 km/h时测点5的相对误差较大，这是因为此处的加速度较其他处小。

5 结论

本文基于连续弹性基础梁理论和温克尔假定，由广义Duhamel公式推导了半无限空间内连续体任一点时频域动力响应函数，得到了轨枕受力数学表达式。借助有限差分软件FLAC 3D分析了隧道底部结构特定监测点的竖向动应力及竖向加速度响应特征。通过将模拟值与实测值对比，验证了所提公式的合理性与适用性，可为隧道底部结构动力响应分析提供一定的理论基础。

[1]王梦恕.中国铁路、隧道与地下空间发展概况[J].隧道建设,2010,30(4):351-364.

[2]彭立敏,覃长炳,施成华,等.铁路隧道基底病害整治现场试验研究[J].中国铁道科学,2005,26(2):39-43.

[3]张玉娥,白宝鸿.高速铁路隧道振动响应数值分析方法[J].振动与冲击,2001,20(3):91-93,102.

[4]梁波,蔡英.不平顺条件下高速铁路路基的动力分析[J].铁道学报,1999,21(2):93-97.

[5]马学宁,梁波,高峰.列车速度对车辆-轨道-路基系统动力特性的影响[J].中国铁道科学,2009,30(2):7-12.

[6]黄娟.基于损伤理论的高速铁路隧道结构振动响应分析及疲劳寿命研究[D].长沙:中南大学,2010.

[7]李军世,李克钏.高速铁路路基动力反应的有限元分析[J].铁道学报,1995,17(1):66-75.

[8]肖鹏,彭立敏,施成华,等.基于车-轨-隧一体化模型的重载铁路隧道动力响应特性分析[J].铁道科学与工程学报,2017,14(6):1263-1271.

[9]李德武,高峰,韩文峰.列车振动下隧道基底合理结构形式的研究[J].岩石力学与工程学报,2004,23(13):2292-2297.

[10]杜明庆,张顶力,房倩,等.铁路隧道仰拱及仰拱填充层动力响应分析[J].中国铁道科学,2016,37(3):38-45.