3-DOF空间机械臂新型滑模轨迹跟踪控制

万凯歌，吴爱国，董娜，方星



3-DOF空间机械臂新型滑模轨迹跟踪控制

万凯歌，吴爱国，董娜，方星

(天津大学 电气与自动化工程学院，天津， 300072)

为了实现机械臂高精度轨迹跟踪，提出一种基于扩展状态观测器(ESO)的新型滑模控制器(PD-ESO-SMC)。该控制器滑模面设计为PD形式，利用ESO对系统的外界的未知干扰、参数的摄动、未建模动态以及耦合部分进行实时估计和补偿，定义并且引入sal函数抑制抖振现象。最后通过稳定性分析证明该控制器的有效性，同时，将仿真结果与基于PD的滑模控制(PD-SMC)及PID控制器进行对比。研究结果表明：所提出的控制方案能实现高精度的轨迹跟踪，对外部干扰有很强的鲁棒性。

机械臂；扩展状态观测器；轨迹跟踪；耦合；滑模控制

机械臂在工业自动化领域扮演着重要的角色，由于对机械臂的控制精度要求越来越高，所以，研究机械臂的高精度的轨迹跟踪具有重要的意义。针对轨迹跟踪问题，研究者提出了很多控制方法，其中滑模控制系统算法简单、响应速度快、对外部噪声干扰和参数摄动具有鲁棒性，在机器人控制领域得到了广泛应用。XU等[1−2]研究将滑模控制器应用于深海作业机械臂，并取得了很好的效果。YAGIZ[3]将滑模控制应用在3-DOF空间机械臂系统，实现了轨迹跟踪。滑模控制由于存在不连续开关特性，因此，会给系统造成“抖振”，并且抖振只能在一定范围内削弱不可能消除，因为消除了抖振也就使系统失去了鲁棒性。于是，人们提出了滑模控制与智能控制相结合的策略来削弱抖振。YAGIZ等[4−5]又将滑模控制与模糊控制相结合，提出了模糊滑模控制策略。张文辉等[6]研究了在不需要模型估计值的情况下对不确定空间机器人轨迹跟踪问题，提出了滑模变结构的神经网络控制方案。但是与智能控制相结合使得控制器的设计较为复杂、成本高，很难在实际中应用。KIM等[7]提出了一种基于干扰观测器(DO)的鲁棒学习控制方法，利用观测器补偿系统的参数摄动、未建模动态以及外部干扰。CHEN等[8]进一步针对机械臂系统提出了基于非线性干扰观测器(NDO)的计算力矩法。VENKATESAN等[9]针对NDO的不足，提出了一种改进的干扰观测器。但是以上这些方法中控制律都包含系统的模型信息。由于3-DOF空间机械臂是强耦合的非线性系统，其精确模型很难获得，所以，在实际应用中，这些方法很难取得较好的效果。在此，本文作者提出基于扩展状态观测器(ESO)的新型滑模控制器(PD-ESO-SMC)。ESO可以对系统的未建模部分、参数的摄动、外界的未知噪声干扰以及耦合部分进行实时估计和补偿，该控制器一个显著特点就是不依赖被控对象的精确模型，并且不削弱系统的鲁棒性。引入并定义1个sal函数，削弱系统的抖振现象。最后，在加入外部干扰条件下将PD-ESO-SMC的仿真结果与PD-SMC及PID的仿真结果进行比较，以验证本文所设计的控制器的优越性。

1 系统模型

机械臂如图1所示。其中：θ为关节角度；和为第2和第3个连杆的重心位置；m，I和L分别为每个连杆的质量、惯性力矩和长度。

1.1 正运动学模型

在参考坐标系下末端坐标可以表示如下：

式中：，和为机械臂末端在参考坐标系下的坐标。

1.2 逆运动学模型

通过求解式(1)可以得到：

1.3 动力学模型

建立拉格朗日方程：

式中：=−；和分别为系统的动能和势能；u为控制力矩分量。由式(3)可以得到系统动力学模型如下所示：

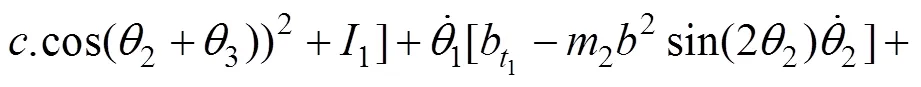
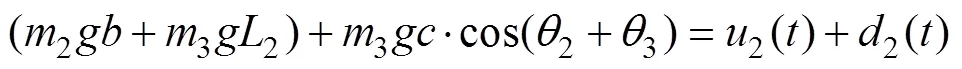
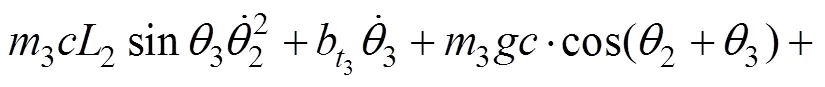
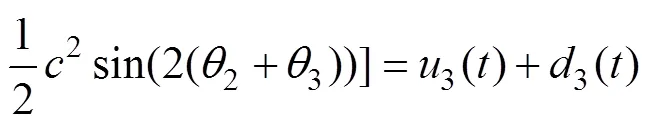
式中：Δ，Δ和Δ表示参数的摄动部分；表示未建模动态部分。进一步将式(8)改写为

定义跟踪误差及其各阶导数如下：

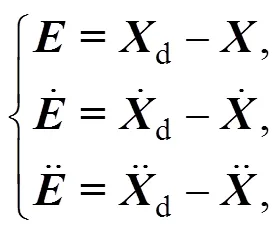
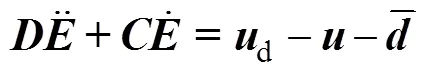
2 控制器设计

从动力学模型可以看出：3-DOF机械臂具有非线性和强耦合性。要想实现解耦比较困难，所以，在存在较大外扰以及机械臂系统的精确动力学模型难以获得的情况下，一些常规的控制方法难以取得较高精度的控制效果。而本文设计的PD-ESO-SMC不依赖被控对象的精确动力学模型，并且将不同关节通道之间的耦合看作扰动并利用扩展状态观测器进行实时估计和补偿[10−12]。所以，可以不用考虑解耦问题，直接针对每个关节通道分别设计控制器就行控制，整个系统的控制原理如图2所示。图2中：d为期望的末端轨迹；d为由期望的末端轨迹经过运动学反解得到期望关节角；为实际输出的关节角；为实际的末端轨迹。

设计PD-ESO-SMC控制器，其中，滑模面设计为

控制律设计为

式中：取值范围为(0，1)。sal函数具有符号函数和指数函数的优点，在误差较大时即离滑模面较远处趋近速度较大，可以使系统快速地到达滑模面。随着系统跟踪误差的减小会逐渐变小，当系统状态接近滑模面时，趋近速度较小，穿过滑模面的速度有限，因此，可以有效削弱系统的抖振。

在进行控制器的设计时参数的选择满足如下参数条件：

图2 机械臂新型滑模控制原理图

Fig. 2 PD-ESO-SMC for spatial robot manipulator

针对式(9)所示的系统，又可以改写为

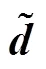
式中：为非线性参数且取值范围为(0，1)；为线性段的区间长度，且有＞0。

3 稳定性分析

定理1 对于如上所述3-DOF机械臂系统，若扰动存在且有界，则适当选择参数值可以实现ESO对干扰的实时观测。

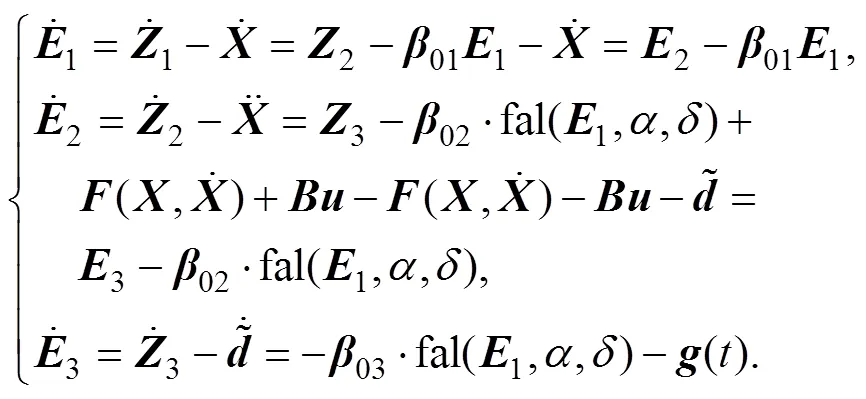
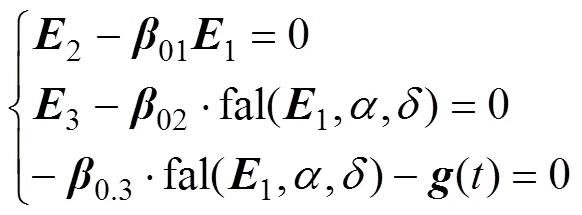
因为fal关于1是单调函数并且fal(0，，)=0，一般先将和根据经验给定为常数，所以，反函数fal−1(0，，)=0。当系统进入稳态后，估计误差为

定理2 对于式(9)所示的机械臂系统，随着扩展状态观测器的引入，能保证滑模面附近的有界运动，可以使系统的状态变量收敛到d附近。

证明 首先证明下面定义成立：

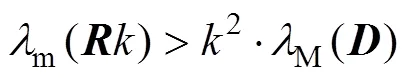
由式(24)可知

再由正定矩阵的性质：

由上式结合正定矩阵得

取李雅普诺夫函数如下:

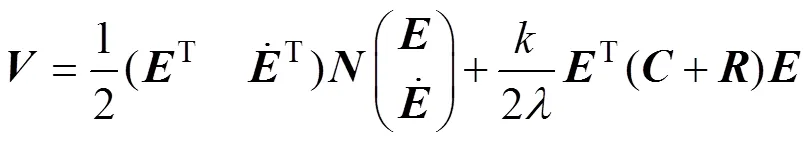
将式(14)代入式(11)得

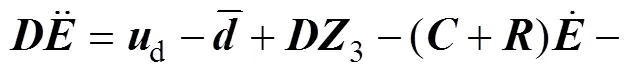
将式(31)代入式(30)得：

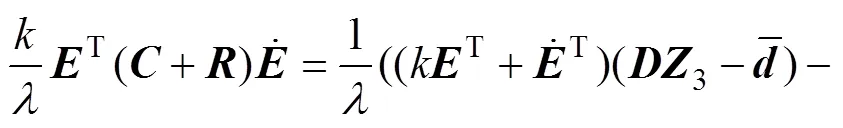
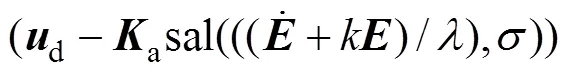
由式(16)知

再由

4 仿真研究

为了验证本文所设计PD-ESO-SMC的有效性，以3-DOF空间机械臂为对象，对其进行了轨迹跟踪的仿真研究。仿真参数为：=0.2，=0.75，=0.5；=8；=2；=diag(90，300，50)，01=diag(30，24，120)，a=diag(50，30，80)，02=diag(1 500，200，800)，03=(1 000，70，6 400)。

PID控制器：

仿真结果如图4所示。机械臂参数如表1所示，机械臂期望的末端轨迹d为

为了验证PD-ESO-SMC的抗扰性能，在仿真中给3个关节通道分别加入1，2和3干扰力矩，如图3所示。扩展状态观测器(ESO)输出如图4所示。从图4可以看出：通道1与其他通道的耦合度较低，主要是外部干扰的影响。通道2和通道3之间的耦合度较高，其中通道2对于外部干扰具有很强的鲁棒性。扩展状态观测器的引入对干扰信号和不同通道间的相互耦合部分以及参数的摄动和未建模动态进行了观测和实时补偿。可以说，扩展状态观测器既实现了干扰观测，又实现了各通道解耦。

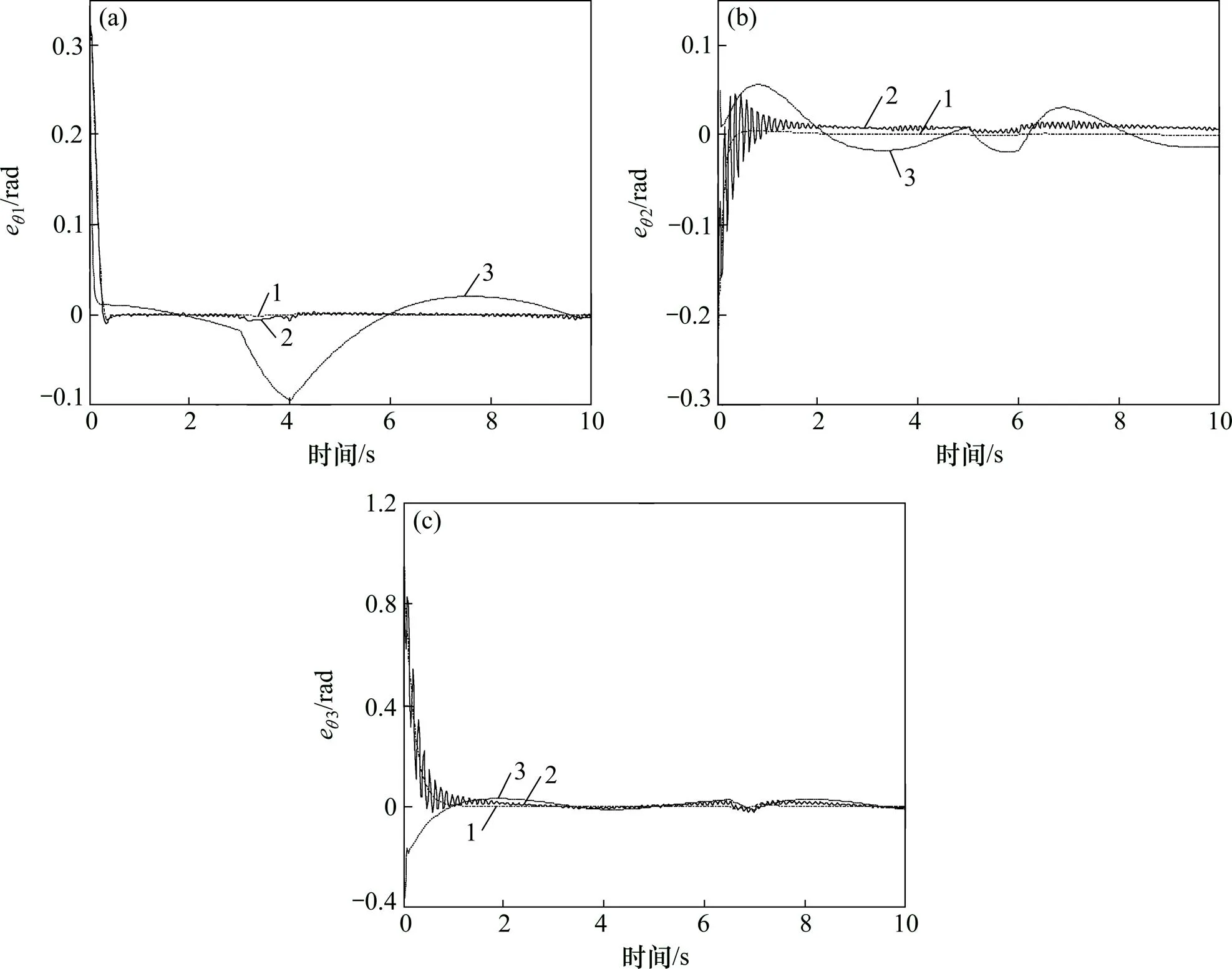
将3种控制方法分别应用于系统，所得关节角跟踪误差见图5。从图5可以看出：本文所设计控制器取得很好的跟踪效果。对于PID控制器，虽然每个关节可以实现无差跟踪，但是对干扰比较敏感、跟踪过程比较震荡。对于PD-SMC控制器，虽然关节实现了快速跟踪，但是不能保证无差跟踪。在加入干扰信号的情况下，外加扰动具有很强的鲁棒性。机械臂轨迹跟踪情况见PD-ESO-SMC控制器可以实现快速无差跟踪，并且对图6，PD-ESM和PD-ESO-SMC的控制力矩比较见 图7。

表1 机械臂参数

由图6可以看出，PD-ESO-SMC与PD-SMC和PID相比能到快速无超调地实现三维空间的轨迹跟踪。从图7可以看出：PD-ESO-SMC采用sal函数能够有效的抑制抖振现象，使得控制输入比PD-SMC控制输入波动较小，有利于保护执行机构。

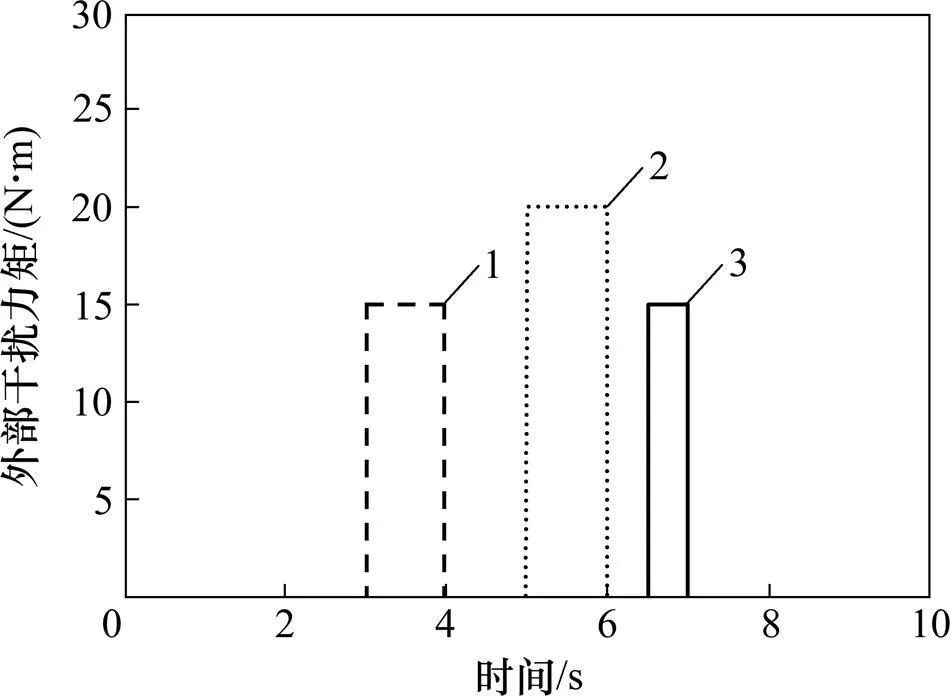
1—d1；2—d2；3—d3。

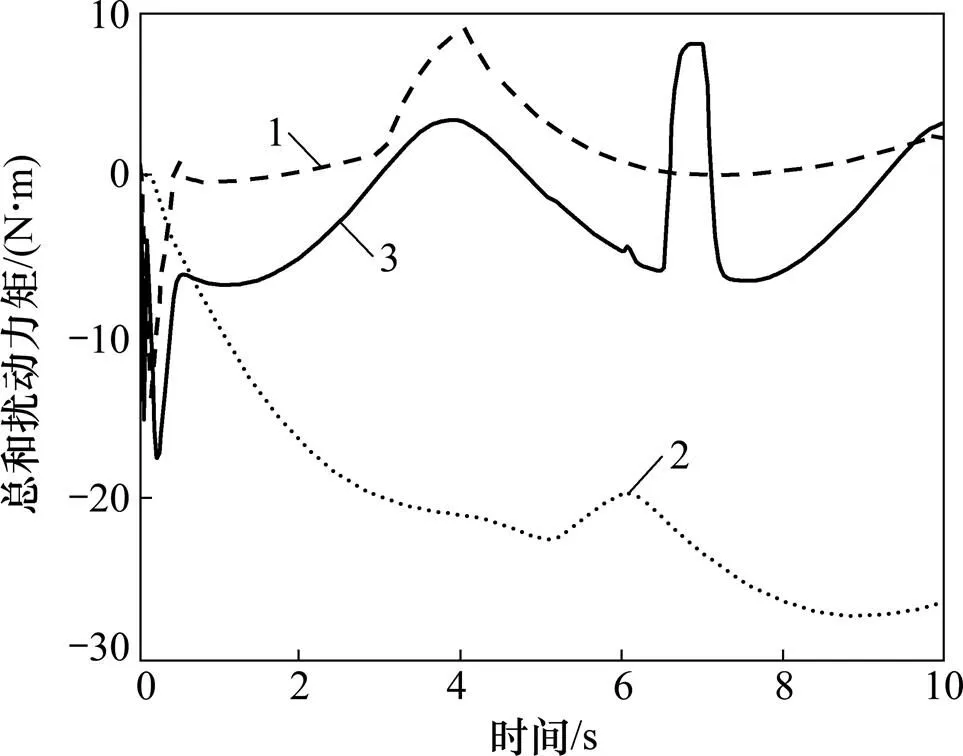
1—观测器1；2—观测器2；3—观测器3。

(a) 关节1；(b) 关节2；(c) 关节3

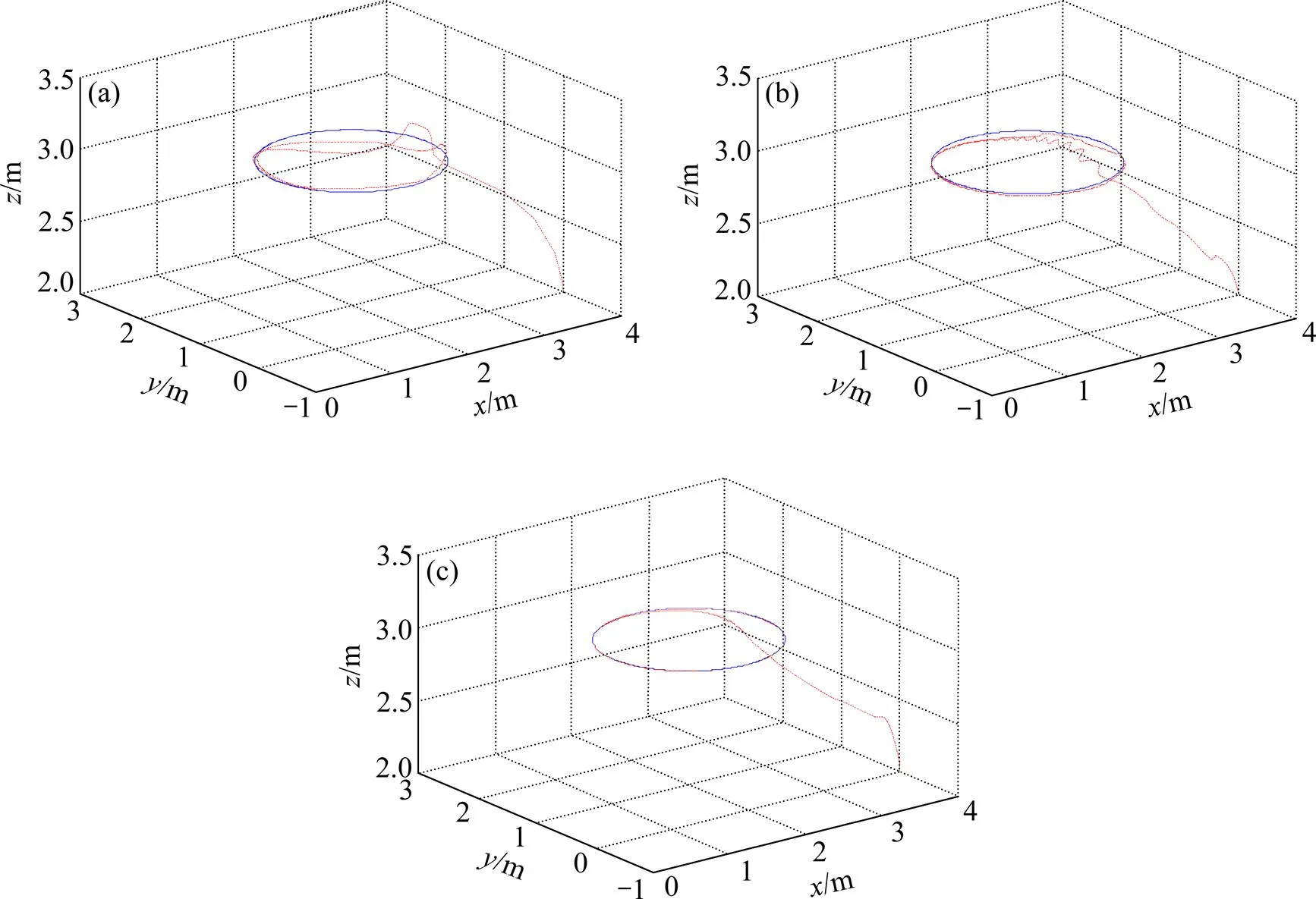
(a) PID控制器空间轨迹跟踪；(b) 滑模控制器空间轨迹跟踪；(c) PD-ESO-SMC空间轨迹跟踪

(a) 关节1；(b) 关节2；(c) 关节3 1—PD-SMC；2—PD-ESO-SMC。

5 结论

1) 建立了3-DOF空间机械臂的运动学和动力学模型，并基于扩展状态观测器和PD控制思想提出了PD-ESO-SMC。

2) 通过引入1个特殊的非线性函数sal来代替传统滑模控制里面的符号函数，能够有效地削弱抖振。

3) 通过对扩展状态观测器的稳定性分析，验证了该控制器的有效性。

4) 该控制器有很强的抗干扰性能。

[1] XU Guohua, XIAO Zhihu, GUO Ying, et al. Trajectory tracking for underwater manipulator using sliding mode control[C]// Robotics and Biomimetics. Sanya, China, 2007: 2127−2132.

[2] ESFAHANI H N, AZIMIRAD V, ESLAMI A, et al. An optimal sliding mode control based on immune-wavelet algorithm for underwater robotic manipulator[C]//2013 21st Iranian Conference on Electrical Engineering (ICEE). Mashhad, Iran, 2013: 1−6

[3] YAGIZ N. Robust control of a spatial robot using sliding modes[J]. Mathematical & Computational Applications, 2002, 7(4): 219−228.

[4] YAGIZ N, HACIOGLU Y. Robust control of a spatial robot using fuzzy sliding modes[J]. Mathematical and Computer Modelling, 2009, 49(1/2): 114−127.

[5] AMER AHMED F, SALLAM ELSAYED A, ELAWADY WAEL M. Adaptive fuzzy sliding mode control using supervisory fuzzy control for 3 DOF planar robot manipulators[J]. Applied Soft Computing, 2011, 11(8): 4943−4953.

[6] 张文辉, 齐乃明, 尹洪亮. 基于滑模变结构的空间机器人神经网络跟踪控制[J]. 控制理论与应用, 2011, 28(9): 1141−1144. ZHANG Wenhua, QI Naiming, YIN Hongliang. Neural network tracking control of space robot based on sliding mode variable structure[J]. Control Theory & Applications, 2011, 28(9): 1141−1144.

[7] KIM B K, CHUNG W K, YOUM Y. Robust learning control for robot manipulators based on disturbance observer[C]// Proceeding of IEEE Industrial Electronics Conference. Taipei, China, 1996: 1276−1282.

[8] CHEN Wenhua, BALANCE D J, GAWTHROP P J. A nonlinear disturbance observer for robotic manipulators[J]. IEEE Transactions Industrial Electronics, 2000, 47(4): 932−938.

[9] VENKATESAN V, MOHAN S, KIM J W. Disturbance observer based terminal sliding mode control of an underwater manipulator[C]//Control Automation Robotics & Vision (IC-ARCV). Singapore, 2014: 1566−1572.

[10] ZHENG Qing, CHEN Zhongzhou, GAO Zhiqiang. A practical approach to disturbance decoupling control[J]. Control Engineering Practice, 2009, 17(9): 1016−1025.

[11] 刘福才, 梁利环, 高娟娟, 等. 不同重力环境的空间机械臂自抗扰轨迹跟踪控制[J]. 控制理论与应用, 2014, 31(3): 352−360. LIU Fucai, LIANG Lihuan, GAO Juanjuan, et al. Trajectory tracking control with active disturbance rejection for space manipulator in different gravity environments[J]. Control Theory & Applications, 2014, 31(3): 352−360.

[12] 韩京清. 自抗扰控制技术[M]. 北京: 国防工业出版社, 2008. HAN Jingqing. Active disturbance rejection control technique[M]. Beijing: Defense Industry Press, 2008.

[13] 黄一, 张文革. 自抗扰控制器的发展 [J]. 控制理论与应用, 2002, 19(4): 485−492. HUANG Yi, ZHANG Wenge. Development of active disturbance rejection controller[J]. Control Theory & Applications, 2002, 19(4): 485−492.

[14] BOYD S, VANDENBERGHE L. Convex optimization[M]. New York: Cambridge University Press, 2004.

[15] OUYANG P R, ACOB J, PANO V. PD with sliding mode control for trajectory tracking of robotic system[J]. Robotics and Computer-Integrated Manufacturing, 2014, 30(2): 189−200.

(编辑 赵俊)

A novel sliding mode controller for trajectory tracking of 3 DOF spatial robot manipulators

WAN Kaige, WU Aiguo, DONG Na, FANG Xing

(School of Electrical Engineering and Automation, Tianjin University, Tianjin 300072, China)

In order to realize the high-precision trajectory tracking, a novel sliding mode controller was presented based on extended state observer (ESO). The controller with sliding mode surface was based on PD. The unknown external disturbance, parameter uncertainty, un-modeling and the coupling were observed and compensated by means of ESO. The chattering problem was attenuated significantly by introducing the function of sal. The effectiveness of the proposed control law was verified by the theoretical analysis of the system stability. The results show that this control algorithm not only realizes the high-precision trajectory tracking as shown in the simulation, but also improves the system robustness in comparison to the PID control and PD with sliding mode control.

robot manipulator; extended state observer; trajectory tracking; coupling; sliding mode control

10.11817/j.issn.1672−7207.2017.12.015

TP242;TP273

A

1672−7207(2017)12−3248−08

2016−12−19；

2017−03−11

国家自然科学基金资助项目(61403274)；天津市应用基础及前沿技术研究计划项目(13JCQNJC03600)(Projects(61403274) supported by the National Natural Science Foundation of China; Project(13JCQNJC03600) supported by the Application Base and Frontier Technology Research Plan of Tianjin of China)

吴爱国，教授，从事机械臂、空调和电机研究；E-mail：agwu@tju.edu.cn