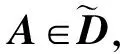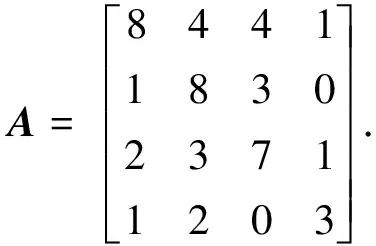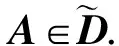非奇异H-矩阵判定的一类充要条件
张俊丽, 韩贵春
(内蒙古民族大学 数学学院, 内蒙古 通辽 028043)
0 引 言
非奇异H-矩阵在控制论、 神经网络系统以及线性时滞系统理论等领域有着广泛应用, 相应系统的稳定性研究经常被转化为判定所对应线性方程组的系数矩阵是否为H-矩阵的研究. 因此,H-矩阵的判定具有重要的意义, 但是在实际问题中判定一个矩阵是否为非奇异H-矩阵很困难. 近年来, 很多学者对该问题作了深入的研究, 得到了一些重要结果[1-10]. 黄廷祝[1]给出了非奇异H-矩阵的简洁判据, 而且很多学者推广了该判据[2,5,8-10]; 文献[8]定义了α对角占优矩阵和α-链对角占优矩阵, 并用其对非奇异H-矩阵进行判定, 之后很多学者在此基础上得到不同形式的非奇异H-矩阵判定准则[5,9], 上述文献给出的判定准则多为充分条件. 本文在文献[1-3]的基础上, 基于对数函数的单调性, 利用非奇异H-矩阵与α链对角占优矩阵关系, 得到非奇异H-矩阵判定的一类充要条件. 该充要条件表现形式简洁, 同时利用数值实验证实了该判定准则的有效性.
用Cn×n表示n×n阶复矩阵的集合.A=(aij)∈Cn×n, 记N={1,2,…,n},
1937年, Ostrowski A M首次给出了H-矩阵的定义.设矩阵A=sI-B,B为非负矩阵, 如果s>ρ(B), 称A为非奇异M矩阵, 其中ρ(B)为矩阵B的谱半径. 令A=(aij)∈Cn×n, 称M(A)=(mij)∈Cn×n为矩阵A的比较矩阵, 其中
如果M(A)为非奇异M矩阵, 称A为非奇异H-矩阵[1].

注1 广义严格对角占优矩阵与非奇异H-矩阵是等价的[4].
定义2[5]设A∈Cn×n, 若∃α∈(0,1], 使得∀i∈N, 有
|aii|≥[Ri(A)]α[Si(A)]1-α,
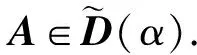
定义3 设A∈D0(α)不可约, 且至少有一个严格不等式成立, 称A为不可约α链对角占优; 若A∈D0(α)且对等式成立的i都存在非零元链αii1,ai1i2,…,aiij, 有
|ajj|>[Rj(A)]α[Sj(A)]1-α,
称A具有非零元链α链对角占优.

①A∈D(α); ② 不可约α链对角占优; ③ 具有非零元链α链对角占优.
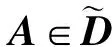
引入符号
N0={i∈N∶|aii|≤Ri(A),|aii|≤Si(A)},
N1={i∈N∶Ri(A)>Si(A)},
N2={i∈N∶Ri(A) N3={i∈N∶Ri(A)=Si(A)}. 易知,N1∪N2∪N3=N. 证明充分性.若∃i∈N1, 满足|aii|≤Si(A), 由Si(A) (2) 若∃j∈N2, 满足|ajj|≤Rj(A), 由Rj(A) (3) 故 (4) (5) 由式(4)和式(5)知, 存在0<α<1, 满足 由此可知, ∀i∈N1, ∀j∈N2, 必定存在0<α<1, 使得式(7)成立. 由式(7)得, ∀i∈N1, 有|aii|>[Ri(A)]α·[Si(A)]1-α; ∀j∈N2, 有|ajj|>[Rj(A)]α·[Sj(A)]1-α. 由N3={i∈N∶Ri(A)=Si(A)},N0=Ø知, ∀i∈N3, 有|aii|>Ri(A)=Si(A). 故∀i∈N3, 有|aii|>[Ri(A)]α[Si(A)]1-α. |aii|>[Ri(A)]α[Si(A)]1-α.(8) 若N0≠Ø, 则∃k∈N0, 有|akk|≤Rk(A), |akk|≤Sk(A), 从而∀α∈(0,1], 有 |akk|≤[Rk(A)]α[Sk(A)]1-α, 与式(8)矛盾, 故N0=Ø. ∀i∈N1, 由式(8)得ln|aii|>αlnRi(A)+(1-α)lnSi(A), 整理得 (9) ∀j∈N2, 由式(8)得 ln|ajj|>αlnRj(A)+(1-α)lnSj(A),(10) 又∀j∈N2, 有Sj(A)>Rj(A), 故lnSj(A)>lnRj(A). 于是 (11) 由式(9)~(11)得式(1)成立. 证明充分性. 若∃j∈N1, 满足|aii|≤Si(A), 则|aii| (13) 故 (14) 若∃j∈N2, 有|ajj|≤Rj(A), 所以|ajj| (15) 由此可知, ∀i∈N1, ∀j∈N2, 存在0<α<1, 使得式(17)成立. 即∀i∈N1, 有|aii|>[Ri(A)]α·[Si(A)]1-α; ∀j∈N2, 有|ajj|>[Rj(A)]α·[Sj(A)]1-α. 仿照定理1, 对∀i∈N3, 有|aii|>[Ri(A)]α·[Si(A)]1-α, 故∀i∈N, 有 |aii|>[Ri(A)]α[Si(A)]1-α. |aii|>[Ri(A)]1-α0[Si(A)]α0,(18) ∀i∈N1, 由式(13)得 (19) ∀j∈N2, 由式(13)得 (20) 由式(19), (20)得式(12)成立. 注2 定理1和定理2可以推广到不可约和具有非零元链的情形, 在此略去. 例 1, 考虑矩阵 计算可得N1={1},N2={2,3},N3=Ø,N0=Ø.利用本文定理 1, 有 例 2, 考虑矩阵 于是,N1={1,4},N2={2,3},N3=Ø,N0=Ø. 利用本文定理 2, 有 [1] 黄廷祝. 非奇异H-矩阵的简捷判据[J]. 计算数学, 1993, 15(3): 318-328. Huang Tingzhu. Some simple determinate conditions for nonsingularH-Matrix[J]. Mathematica Numerica Sinica, 1993, 15(3): 318-328. (in Chinese) [2] 王峰. 非奇异H-矩阵判定的迭代准则[J]. 安徽大学学报(自然科学版), 2011, 36(6): 16-20. Wang Feng. New iterative codes for nonsingularH-matrices[J]. Journal of Anhui University (Natural Science Edition), 2011, 36(6): 16-20. (in Chinese) [3] 邰志艳, 李庆春, 胡硕.α-对角占优矩阵的等价表征及应用[J]. 吉林大学学报(理学版), 2015, 53(5): 934-938. Tai Zhiyan, Li Qingchun, Hu Shuo. Equivalent representations ofα-diagonally dominant matrices and its applications[J]. Journal of Jilin University (Science Edition), 2015, 53(5): 934-938. (in Chinese) [4] Berman A, Plemmons R J. Nonnegative matrix in the mathematical sciences[M]. New York: Academic Press, 1979. [5] 周伟伟, 徐仲. 非奇H-矩阵细分迭代准则[J]. 数值计算与计算机应用, 2011, 32(4): 293-300. Zhou Weiwei, Xu Zhong. Subdivided and an iterative code for nonsingularH-matrices[J]. Journal on Numerical Methods and Computer, 2011, 32(4): 293-300. (in Chinese) [6] 孙玉祥. 广义对角占优矩阵的充分条件[J]. 高等学校计算数学学报, 1997, 9(3): 216-223. Sun Yuxiang. Sufficient conditions for generalized diagonally dominant matrices[J]. Numerical Mathematics A Journal of Chinese Universities, 1997, 9(3): 216-223. (in Chinese) [7] Sun Yuxiang. An improvement on a theorem by ostrowski and its applications[J]. Northeastern Mathematical Journal, 1991, 7(4): 497-520. [8] 李继承, 张文修. H矩阵的判定[J]. 高等学校计算数学学报, 1999, 21(3): 264-268. Li Jicheng, Zhang Wenxiu. Criteria forH-matrices[J]. Numerical Mathematics A Journal of Chinese Universities, 1999, 21(3): 264-268. (in Chinese) [9] 张俊丽, 韩贵春. 一类非奇H-矩阵的迭代判定准则[J]. 河南科技大学学报(自然科学版), 2016, 37(1): 88-91. Zhang Junli, Han Guichun. Iterative criteria for a kind of nonsingularH-matrices[J]. Henan University of Science and Technology (Natural Science Edition), 2016, 37(1): 88-91. (in Chinese) [10] 兰溪, 孙玉祥. 非奇异H矩阵的实用判定[J]. 大学数学, 2010, 26(5): 109-111. Lan Xi, Sun Yuxiang. Practical criterion for nonsingularH-matrices[J]. Colloge Mathematics, 2010, 26(5): 109-111. (in Chinese)1 主要结果
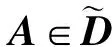
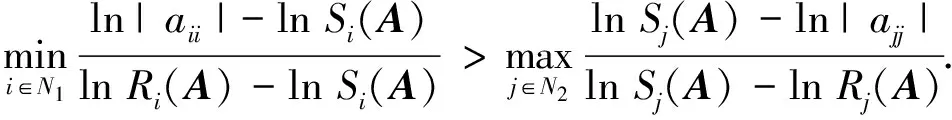
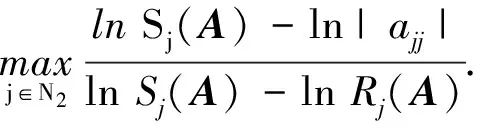
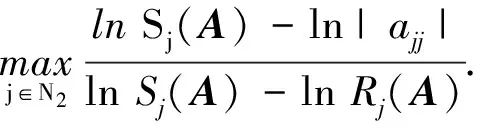

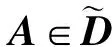
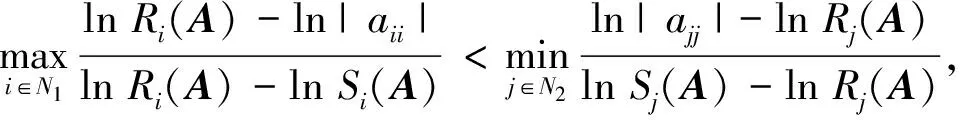
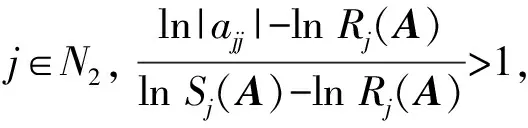
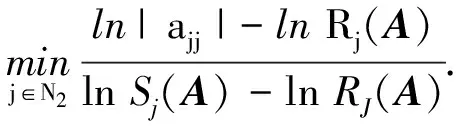

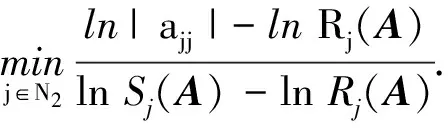
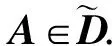
2 数值算例