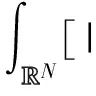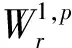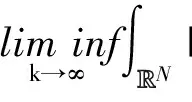一类临界拟线性椭圆型方程非平凡解的存在性

杨晓枫， 腾凯民

(太原理工大学 数学学院， 山西 太原 030024)

0 引 言

本文研究带临界Sobolev指数的拟线性椭圆型方程

-Δpu-(Δpu2)u+|u|p-2u=

k(|x|)|u|2p*-2u,x∈RN,(1)

κ△(h(|ψ|2))h′(|ψ|2)ψ-f(|ψ|2)ψ,(2)

式中：W(x)是给定的位势；κ是一个实数, 且f,h都是实函数. 当h不同时, 拟线性薛定谔方程(2) 对应不同的物理模型， 可被用于等离子物理超流体膜的研究中[1], 也常出现在量子力学[2]和凝聚态理论[3]中等.

当κ=0时, 方程(2)简化为经典的薛定谔方程, 也是量子力学的基本方程. 关于其驻波解的研究, 在对位势和非线性项给予不同的假设条件下, 20世纪70年代以来, 许多学者采用变分方法对此方程作了大量的研究工作.

当κ≠0且p=2时, Poppenberg和Schmitt采用约束极小方法证明了基态解的存在性[4]. 刘嘉荃和王志强引入对偶变换, 使拟线性问题转化成半线性问题, 同时， 在Orlicz空间的框架下采用山路定理证明了其正解的存在性[5]. 与此同时, Colin和Jeanjean也引入了变量代换的方法, 选取Sobolev空间H1(RN)为工作空间, 利用山路定理证明了正解的存在性[6]. 至此, 变量代换方法成为研究此类拟线性方程的基本工具. 杨敏波和丁彦恒采用极小极大方法, 证明了当ε≤ε0时方程正解的存在性以及当ε≤εm时方程解的多重性[7]. 刘祥清等运用Nehari Manifold建立了变号基态解的存在性[8]. 贺小明等利用Nehari Manifold以及Lyusternik-Schnirelmann畴数理论研究了临界增长的拟线性薛定谔方程基态解的存在性、 多重性及其集中性[9]. 另外, Medeiros等应用Ekeland变分原理、 山路定理和Trudinger-Moser不等式证明了两个正解的存在性[10]. 当p≥2时, Alves和Figueiredo采用极小极大的方法与Lyusternik-Schnirelmann畴数理论研究了次临界增长的拟线性方程解的多重性问题[11]. 对方程(1)的研究, 可参考一些文献[12-14].

本文的主要研究目的是建立临界问题的无穷远集中紧性原理, 并应用该原理结合约束极小化方法研究方程(1)非平凡解的存在性. 本文的结果推广了前人关于薛定谔方程研究的结果[15].

本文首先介绍了变分框架, 然后通过变量替换重述了这个问题， 最后利用无穷远集中紧性原理和极小化方法证明了主要结果.

1 预备知识和变分框架

本文对位势k(|x|)作假设(K)

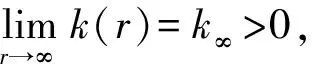
我们引入Sobolev空间

W1,p(RN)=u∈Lp(RN)|u∈Lp(RN),

其上赋予范数

形式上, 方程(1)具有如式(3)的能量泛函

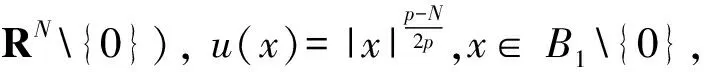
2) 当t∈(-∞,0]时,f(-t)=-f(t).

那么, 通过该变量代换, 泛函I(u)可以被重写为式(4)

J(v)∶=I(f(v))=

当位势k(x)满足假设(K)时, 泛函J(v)在整个Sobolev空间W1,p(RN)上是有定义的, 通过直接计算, 可知J∈C1(W1,p(RN),R)以及对任意的v,φ∈W1,p(RN)有

|f(v)|p-2f(v)f′(v)φ]dx-

因此, 泛函J的临界点对应方程(6)的弱解

-Δpv+|f(v)|p-2f(v)f′(v)=

k(|x|)|f(v)|2p*-2f(v)f′(v).(6)

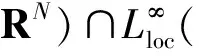
引理1 函数f及其导数具有的性质有：

1)f是定义在C∞上的函数且可逆.

3) 对于所有的t∈R， 都有|f(t)|≤|t|.

5) 存在一个正常数C， 有

6) 对于所有的t∈R, 存在a>0, 使f2(t)≤a|t|.

RN)=v∈W1,p(RN)|v是径向函数,

其上赋予范数

2 主要结果及其证明

我们首先陈述关于方程(6)的主要结果, 其次建立这类拟线性问题的无穷远的集中紧性原理, 并应用该集中紧性原理得到极小化序列的“紧性”.

本文的主要结果陈述如下.

即v是方程(7)的弱解.

-Δpv+|f(v)|p-2f(v)f′(v)=μk(|x|)|f(v)|2p*-2f(v)f′(v),x∈RN.(7)

注采用约束极小化方法找到极小元后, 应用拉格朗日乘子定理会产生一个参数μ∈R. 事实上, 方程(1)右端非线性项化为一个非齐次项k(|x|)|f(v)|2p*,导致不能采用尺度变换把该极小元转化为方程(1)的解,使拉格朗日常数不能消去.

定义

2) 对于每一个j∈N,j≥1, 当k→∞时, 下面序列的极限都是有限的,

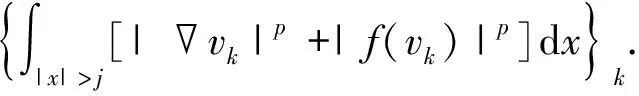
下面说明vk在Lp(RN)上有界. 由引理1(5)得,

2) 这一部分的证明过程可参考相关文献[15].

应用单调有界原理, 可推导出下面的引理.

引理3 下列极限存在且有限, 并有α0,α∞∈[0,1].

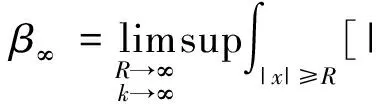
引理4 下列估计成立:

证明1) 对于每一个k∈N和R>1, 有

C3RN.(8)

结合有界控制收敛定理, 得

令k→∞, 得

对于每一个k和每一个j有

(9)

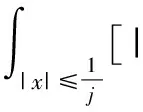
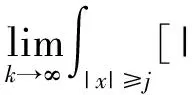
对任意f(vk)∈Lp(RN), 由引理1(3)得φRvk∈Lp(RN),f(φRvk)∈Lp(RN). 另外, 我们知道

由φR有界,vk∈Lp(RN), 很明显有φRvk∈Lp(RN), 再由Hölder不等式容易推得|vkφR|∈Lp(RN), 则(φRvk)∈Lp(RN), 那么RN).

首先考察不等式左边, 有

再考察不等式右边, 有

|(φRvk)|p=|vkφR+φRvk|p.

由式(8)及有界控制收敛定理， 得

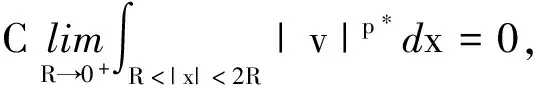
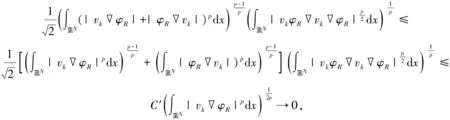
另外,

那么, 结合式(11)和(12)可得,

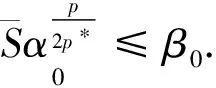
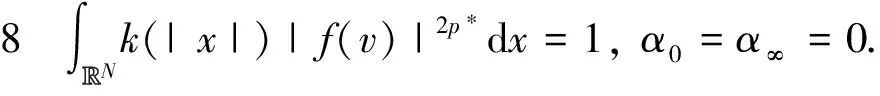
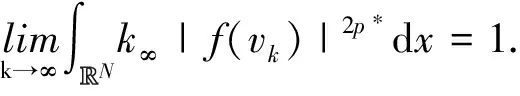
结合式(8)可得, 在有界开集Aε=x∈RN|x|

⟹

由ε的任意性， 得

⟹

再由Sb的定义, 得

与引理6矛盾. 因此, 结论得证.

下证参数μ>0. 事实上, 由方程(7)得

[1] Kurihura S. Large-amplitude quasi-solitons in superfiuids films[J]. Journal of the Physical Society of Japan, 1981, 50(50)： 3262-3267.

[2] Hasse R W. A general method for the solution of nonlinear soliton and kink Schrödinger equation[J]. Zeitschrift Für Physik B Condensed Matter, 1980, 37(1)： 83-87.

[3] Makhankov V G, Fedyanin V K. Non-linear effects in quasi-one-dimensional models of condensed matter theory[J]. Physics Reports, 1984, 104(1)： 1-86.

[4] Poppenberg M, Schmitt K, Wang Z Q. On the existence of soliton solutions to quasilinear Schrödinger equations[J]. Calculus of Variations Partial Differential Equations, 2002, 14(3)： 329-344.

[5] Liu J Q, Wang Y Q, Wang Z Q. Soliton solutions for quasilinear Schrödinger equations II[J]. Journal of Differential Equations, 2003, 187(2)： 473-493.

[6] Colin M, Jeanjean L. Solutions for a quasilinear Schrödinger equation： a dual approach[J]. Nonlinear Analysis, 2004, 56(2)： 213-226.

[7] Yang M B, Ding Y H. Existence of semiclassical states for a quasilinear Schrödinger equation with critical exponent inRN[J]. Annali Di Matematica Pura Applicata, 2013, 192(5)： 783-804.

[8] Liu X Q, Liu J Q, Wang Z Q. Ground states for quasilinear Schrödinger equations with critical growth[J]. Calculus of Variations Partial Differrential Equations, 2013, 46(3-4)： 641-669.

[9] He X M, Qian A X, Zou W M. Existence and concentration of positive solutions for quasilinear Schrödinger equations with critical growth[J]. Nonlinearity, 2013, 26(12)： 3137-3168.

[11] Alves C O, Figueiredo G M, Severo U B. Multiplicity of positive solutions for a class of quasilinear problems[J]. Advances in Differetial Equations, 2009, 10： 911-942.

[12] Wu K, Zhou F. Existence of ground state solutions for a quasilinear Schrödinger equation with criticial growth[J]. Computers and Mathematics with Applications, 2015, 69(2)： 81-88.

[13] Pei R, Zhang J. Nontrivial solutions for a class of quasilinear elliptic equations[J]. Journal of Mathematical Research with Applications, 2016, 36(1): 87-96.

[14] Alves C O, Figueirdeo G M. Multiple solutions for a quasilinear schrödinger equation onRN[J]. Acta Applicandae Mathematicae, 2015, 136: 91-117.

[15] Badiale M, Serra E. Semilinear Elliptic Equations for Beginners[M]. London： Springer-Verlag, 2011.

[16] Zhu X P, Yang J F. Regularity for quasilinear elliptic equations involving critical Sobolev exponent[J]. Journal of System Science and Mathematical Science, 1989, 9(1)： 47-52.