“矩阵与变换”高考复习课堂在线

王小青

一、聚焦考纲

1.了解二階矩阵的概念，了解线性变换与二阶矩阵之间的关系.

2.了解旋转变换、反射变换、伸缩变换、投影变换、切变变换这五种变换的概念与矩阵表示.

3.理解变换的复合与矩阵的乘法；理解二阶矩阵的乘法和简单性质.

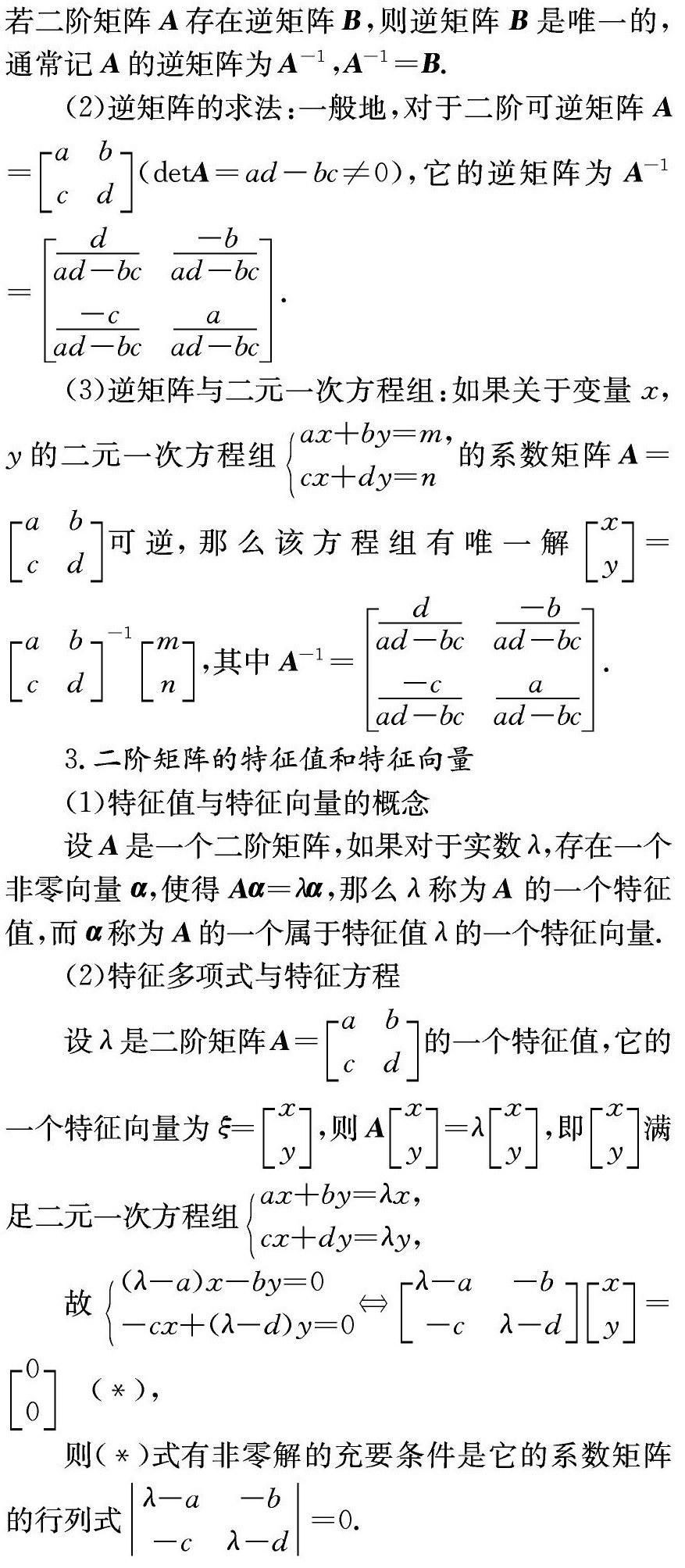
4.理解逆矩阵的意义，会求出简单二阶逆矩阵.

5.理解矩阵的特征值与特征向量，会求二阶矩阵的特征值与特征向量.

二、知识梳理

1.矩阵的乘法规则

评注：（1）设A是一个二阶矩阵，α是矩阵A的属于特征值λ的任意一个特征向量，则Anα=λnα（n∈N*）.（2）设λ1，λ2是二阶矩阵的两个不同特征值，ξ1，ξ2是矩阵的分别属于特征值λ1，λ2的特征向量，对于任意的非零平面向量α，设α=t1ξ1+t2ξ2（其中t1，t2为实数），则对任意的正整数n，有Anα=t1λn1ξ1+t2λn2ξ2.（3）对于求解Anα的问题，一般可利用矩阵的特征值求特征向量来解决，对n较小的情况，也可直接采用矩阵乘法来解决.

四、规律总结

1.矩阵相等实质上是矩阵对应元素相等，体现了方程思想，要注意矩阵对应元素相等.

2.矩阵的乘法只满足结合律，不满足交换律和消去律.

3.对于平面图形的变换要分清是伸缩、反射、还是切变变换.

4.伸缩、反射、切变变换这三种几何变换称为初等变换，对应的变换矩阵为初等变换矩阵，由矩阵的乘法可以看出，矩阵的乘法对应于变换的复合，一一对应的平面变换都可以看作这三种初等变换的一次或多次的复合.

5.逆矩阵的求法常用待定系数法.

6.若A，B两个矩阵均存在可逆矩阵，则有（AB）-1=B-1A-1，若A，B，C为二阶矩阵且A可逆，则当AB=AC时，有B=C，即此时矩阵乘法的消去律成立.

7.求Mnα，一般都是先求出矩阵M的特征值与特征向量，将α写成t1α1+t2α2.利用性质，Mnα=t1λn1α1+t2λn2α2求解.