让人琢磨不透的“无穷”

竹林风

“无穷”的本意是很多很多的意思，它有着神奇的魔力。一旦牵扯到它，就会出现各种不可思议的事情。走，一起去瞧瞧吧！对了，记得唤醒你的脑细胞并托好你的下巴！奇妙有趣的事就要发生了……

奇怪的旅店

相传有这样一家旅店，它设有无穷多个房间，房间号从1开始，无限制地排下去。也正因如此，它被称为“无穷旅店”。

一天深夜，约翰走进了这家旅店，想要一间房。

“真不好意思，约翰先生！所有房间都住满了客人。”旅馆老板微笑地回应，“不过，如果您愿意给我一点儿时间，或许我可以为您腾出一间房来。”

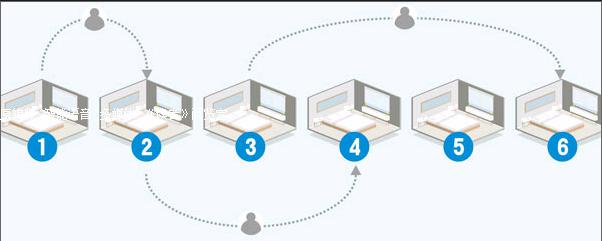
说完，旅馆老板便离开自己的办公台，很不好意思地叫醒了已睡下的客人，并请他们换房间：1号房间的客人搬到2号房间，2号房间的客人搬到3号房间……n号房间的客人搬到（n+1）号房间。就这样，1号房间被腾空了出来，约翰顺利入住。

或许因为正值旅行旺季，周末来了一个“无穷旅行团”，成员人数与正整数一样多。这时，刚才的应急措施行不通了，旅店老板还有办法安顿他们吗？

当然！这回他请1号房间的客人住到2号房间，2号房间的客人住到4号房间，3号房间的客人住到6号房间。这样，所有奇数号的房间都空出来了，正好可以安排给 “无穷旅行团”的成员住下。

客人们都没退房，可紧接着又来了无穷多个“无穷旅行团”。大家应该会想：这次旅店老板应该没辙了吧！不，他想出了一条妙计，照样把无穷多个“无穷旅行团”的成员安排住下了。

原来他是这么安排的：

先假设（m，n）（其中m=1，2，3…）表示第m个旅行团的第n个成员，则

第1个旅行团中的成员为：（1，1）（1，2）（1，3）（1，4）…

第2个旅行团中的成员为：（2，1）（2，2）（2，3）（2，4）…

……

第m个旅行团中的成员为：（m，1）（m，2）（m，3）（m，4）…

然后按下图中箭头的顺序，每人住进安排的1号、2号、3号、4号……房间，这样便可让所有旅行团的成员都有房间住。

偶数VS自然数

问：偶数有多少个？

答：无穷个。

问：自然数有多少个？

答：无穷个。

问：偶数与自然数，哪一种数多？

答：这个……

对于这个问题，恐怕有不少同学会说：“当然是自然数比偶数多了，因为偶数的个数等于自然数个数的一半。”大家为什么会这么说呢？因为奇数与偶数合起来就是自然数，而奇数与偶数是相间排列的，所以奇数和偶数一样多，都是自然数的一半。

自然数包括偶数，偶数是自然数的一部分，自然数的个数比偶数多这不是显而易见、再明白不過的事吗？听起来好像确实是这么一回事，可事实是不是这样的呢？

16世纪，意大利著名科学家伽利略给出了正确的答案：偶数和自然数一样多。这似乎违背常识，因为在1～10中，你只要数一下，就可以知道自然数有10个，偶数有5个，很显然，自然数的个数比偶数的个数多5个。但大家可别忘了，这是在有限的情况下，毕竟自然数和偶数可远不止那几个，而是无穷个。于是，对于两个无限的数量，数数的办法是行不通了，因为无穷个是永远数不完的。

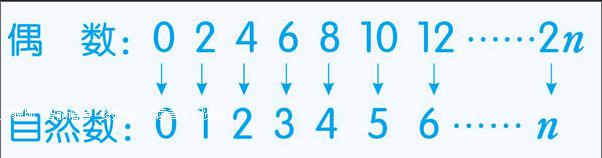
有什么办法可以比较它们的数量呢？经过一番苦思冥想，有了！我们可以用配对的办法来比较。对，这种方法同样可以用在无限上，关键要看比较的两部分之间能否建立起一一对应的关系。如果能建立，那么我们就可以认为两者的数量相等。伽利略在自然数与偶数之间建立了如下的对应关系——

看，给出一个偶数，我们可以找出一个自然数与之对应，给出的偶数不同，与之相对应的自然数也不同；反过来，对于每一个自然数，我们都可以找到一个偶数与其对应，自然数不同，所对应的偶数也不同。由此可见，偶数与自然数之间建立了一一对应的关系，所以，偶数与自然数一样多。

有没有很意外？这就是“伽利略悖论”。在无限中，“部分”可以等于“整体”。如果一个量等于它的一部分量，那么这个量必是无限量；反之，无限量必然可以等于它的某一部分量。

奇妙有趣的事是一件接一件的，继续往下看吧！endprint