船载卫星通信天线伺服跟踪环路设计

杨 丽，李 莉，孙宏强，卢智嘉

(石家庄学院 机电学院，河北 石家庄 050035)

0 引言

船载卫星通信天线在舰船航行过程中能够实现实时跟踪同步卫星，同时连续传递文字、图像、语音、数据等多媒体信息，用于满足各种军民通信需要。在舰船航行过程中，由于船体姿态数据和地理位置数据发生变化，会使天线指向偏离卫星理论位置，使天线跟踪丢失，因此天线必须实时跟踪指向目标来隔离船体姿态数据和地理位置数据的变化[1]。船载天线的跟踪方式有很多种，常用的有单脉冲差信号跟踪、程序引导跟踪、极大值跟踪、幅面圆锥扫描跟踪等。本文以A-E两轴座架天线单脉冲差信号跟踪为例说明天线伺服跟踪环路设计，为后续工程实践提供参考依据。

1 伺服控制设备组成

伺服控制的设备配置如图1所示，由北斗(GPS)、姿态仪(惯导)、计算机、方位、俯仰、极化三个独立控制支路等组成[2]。

图1 系统组成

2 自动捕星

根据GPS(或北斗)提供的舰船地理位置(经度、纬度)和星位(经度)信息，计算出天线指向卫星的地理方位角A、俯仰角E；根据舰船姿态测量装置提供的舰船姿态信息，将地理方位、俯仰角转化成舰船坐标方位轴角Aj、俯仰轴角Ej，以Aj、Ej作为指令角控制天线指向卫星，使卫星进入天线3dB波束宽度内，实现捕星，在捕获卫星后使跟踪接收机锁定，伺服系统自动转入自跟踪状态[3]。

(1)地理方位角A、俯仰角E和极化角P的计算

式中：λ0：星经度；λ1：车经度；φ：车纬度；r：地球半径；R：同步轨道半径；r/R：0.1503。

(2) 将地理角转换为车体坐标角

Ej=sin-1(cosRcosPsinE-cos(A-H)cosEsinPcosR+sin(A-H)cosEsinR)

其中：Aj、Ej为天线对星的舰船坐标角；A、E为天线对星的地理坐标角；R、P、H为舰船姿态的横滚角、纵倾角、航向角。

3 跟踪精度分析

(1)天线方位、俯仰轴跟踪精度指标

对于A-E两轴座架天线，跟踪误差是A、E轴误差的合成，如下式所示：

其中：Δθ为天线指向误差，ΔθA、ΔθE为天线方位轴误差、俯仰轴误差。

如果按天线指向误差在A、E轴上等概率分布考虑，则分配到A、E轴的误差为：

ΔθA=ΔθE=Δθ

由此可确定：要满足天线跟踪精度的要求，只要A轴误差ΔθA、E轴误差ΔθE不超过Δθ即可满足天线跟踪精度要求，这就是分配到A、E轴的指标要求。

天线的3dB波束宽度：

其中：θ0.5：天线的3dB波束宽度，单位-°;D：天线口径，单位-m;f：天线工作频率，单位-GHz

对于Ku频段0.8m天线，天线的3dB波束宽度约为：2.1°，如果跟踪精度要求1/10波束宽度，即0.21°。跟踪误差在A、E轴等概率分布，则有：

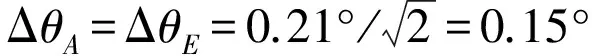
(2)舰船姿态变化对A、E轴的影响

如果舰船姿态近似按正余弦规律变化，按横、纵倾变化角度5°、周期1s考虑，则舰船在横倾、纵倾姿态变化的最大角速度和最大角加速度分别为：

最大角速度为：

横倾最大角速度(ΩR)max=31.4°/s

纵倾最大角速度(ΩP)max=31.4°/s

最大角加速度为：

横倾最大角加速度(αR)max=197.2°/s2

纵倾最大角加速度(αP)max=197.2°/s2

(3)姿态变化角速度对A、E轴影响

角速度影响：

投影到E轴的最大角速度：(ΩE)max=44.4°/s

投影到A轴的最大角速度：(ΩA)max=(ΩE)max tgE=77°/s

角加速度影响

姿态变化角加速度对A、E轴影响的最大角加速度有同样的关系：

投影到E轴的最大角加速度：(αE)max=278°/s2

投影到A轴的最大角加速度：(αA)max=(αE)maxtgE=483°/s2

(4)姿态变化在A、E轴上带来的最大指向角变化

方位轴、俯仰轴运动角频率分别为：

ωA=(αA)max/(ΩA)max=483/77=6.28

ωE=(αE)max/(ΩE)max=278/44.4=6.28

当天线工作在俯仰60°时，根据投影关系可推算出舰船姿态变化在A、E轴上带来的最大指向变化分别为：

(θA)max=(ΩA)max/ωA=77/6.28=12.3°

(θE)max=(ΩE)max/ωA=44.4/6.28=7°

图2 幅频特性波特图

(5)环路隔离度要求

要求的隔离度为：

也就是说，要求方位轴伺服环路幅频特性波特图在角频率小于6.28时，不能进入39dB这个区域，如图2所示。

同理，俯仰轴伺服环路幅频特性波特图在角频率小于6.28时，不能进入34dB的区域，这就是伺服环路设计的依据。

4 隔离度分配

伺服环路的隔离度包含自跟踪环隔离度和陀螺环隔离度的贡献。由于受到天线接收信号信噪比的限制，自跟踪环的带宽相对来说较窄，其隔离度贡献较小，所以伺服环路的隔离度主要来自于陀螺环，隔离度分配如下：

方位轴：陀螺环33 dB，自跟踪环6 dB

俯仰轴：陀螺环28 dB，自跟踪环6 dB

控制环路如图3所示。

图3 控制环路图

W1(S) ：陀螺环校正电路 W2(S)：速度环校正

H：陀螺反馈系数 β：速度反馈

1/i：减速器速比 f ：姿态扰动

速度环作为陀螺环的内环，其闭环传递函数可近似为一阶惯性环节如下式，其幅频特性波特图如图4中曲线1所示：

陀螺环固有传递函数为：

KT0= Kn*(1/i)*H

20lgKT0= 20lg(6×0.2) = 1.5dB

其幅频特性波特图如图4中曲线2所示。

引入串联校正电路后，陀螺环传递函数为：

WT(S) = W1(S)*WT0(S)

WT(S)：陀螺环传递函数

W1(S)：串联校正电路传递函数

WT0(S)：陀螺环故有传递函数

陀螺环如图5所示，串联校正电路其传递函数为：

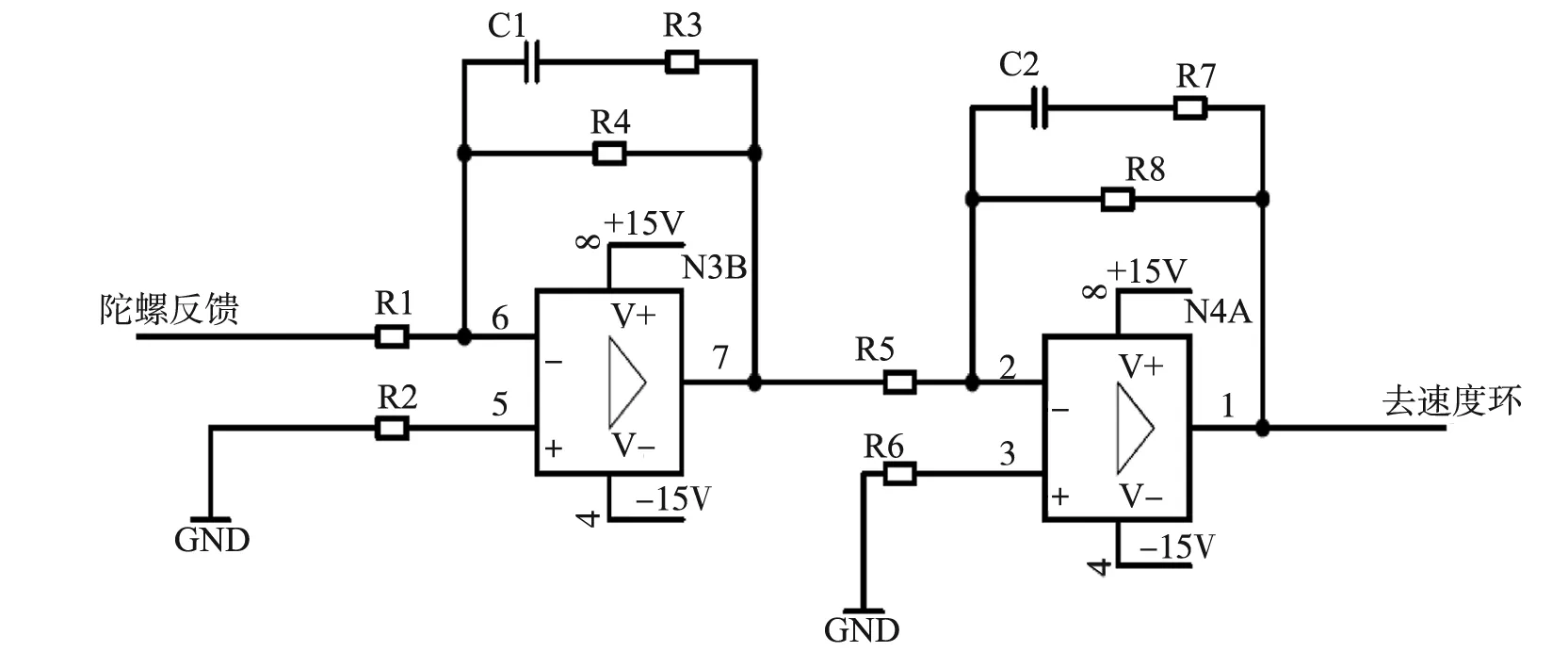
图5 陀螺环

K1=R4/R1 K2=R8/R5

=R3·C1 =R7·C2

=(R3+R4)·C1 =(R7+R8)·C2

陀螺环开环传递函数为：

KT=K1*K2*KT0

L(KT)=20lg(K1*K2*KT0)

陀螺环特性：通过选择校正电路的电阻电容，使陀螺环开环频率特性波特图在角频率小于6.28时保持大于33dB(方位轴)，如图6中曲线1所示，这就是陀螺环预期开环频率特性。

图6 幅频特性波特图

跟踪环特性：自跟踪环是陀螺环的外环，在陀螺稳定的基础上对姿态变化进一步隔离，它是一个空间位置闭环控制环路，能够修正陀螺漂移及地理位置变化带来的指向慢速变化。由于受到接收信号信噪比的限制，自跟踪环带宽相对较窄，即要求在角频率6.28处其环路增益要大于6dB；同时，为了减小陀螺漂移的影响，在低频段增益要尽量提高，跟踪环曲线如图6中曲线2所示。

5 结束语

本文以船载A-E两轴座架天线为例，详细论述了天线伺服控制的环路设计，并在实践中得到很好的验证，为工程实践提供了理论设计依据。

[1] 万冰.船载“动中通”通信地球站天线及其跟踪系统研究与设计[C].南京:南京邮电大学,2015.

[2] 章百宝,陈涛.某卫星通信天线伺服系统的设计与实现[J].现代电子技术,2015,38(1):59-61.

[3] 岳翔宇,云帆.高精度卫星天线自控系统的设计与实现[J].电视工程,2014,(1):41-43.