旋涡泵压力脉动特性的研究
俞 健,秦子明,方 超,蔡标华,张 露,吴大转
(1.武汉第二船舶设计研究所,湖北武汉 430064;2.浙江大学,浙江杭州 310027)
1 前言
旋涡泵,又可称为再生泵、涡轮泵、圆周泵和摩擦泵。旋涡泵一方面具有离心泵达不到的低比转速,另一方面比容积式泵具有更好的压力脉动性能和可维护性,其逐渐代替容积式泵被广泛应用为高压小流量系统的流体输送泵。
旋涡泵因其小流量、高扬程的特点得到国内外学者越来越多的关注。A Engeda等对旋涡泵的内部复杂流动提出了理论数学模型和算法[1,2]。Francis J Quail等对轴向流动的旋涡泵进行了研究,提出了旋涡泵内流体动量交换的一维模型,并通过试验验证[3],后又结合一维模型和三维数值模拟,提出了旋涡泵的设计方案[4],同时提出了旋涡泵复杂叶轮的成型方法[5]。王洋等通过数值模拟的方法讨论了闭式叶轮的叶片位置对旋涡泵性能的影响[6]。沙溢等通过试验验证了相似理论对于旋涡泵性能判断的适用性[7]。张菲茜等通过数值模拟的方法计算了用于燃油系统的微型旋涡泵的水力性能并分析了叶轮的承载机理[8]。因此,旋涡泵的理论分析和性能研究在国内外得到了广泛关注,并且在燃油系统上也得到了大量应用,然而对于旋涡泵的压力脉动特性研究则相对较少。研究表明,旋涡泵产生的尖锐的噪声大部分来源于内部流体与进出口分隔区即阻隔面的动静干涉[9]。压力脉动频谱图与流动噪声是一致的,因而流动噪声可以通过研究压力脉动来预测[10]。因此,通过旋涡泵的压力脉动特性的研究和控制,可为旋涡泵由流体脉动诱发的振动噪声控制提供解决方案。
将动静干涉诱导压力脉动与减振降噪结合的研究极为广泛,其主要研究对象是离心泵和风机。其中,非等距叶片分布也得到了越来越多学者的关注,如河合勇太等对随机分布法则进行了统计分析,归纳出适用于汽车供油泵的叶片分布规律[11]。武鹏等通过数值模拟研究在非等距叶片分布下微型旋涡泵压力脉动特性[12]。非等距分布方法,是指通过打乱叶片的周期分布方式,使相邻的叶片夹角产生差值,从而削弱动部件与静部件干涉作用的方法。本文通过随机分布法则对旋涡泵均布叶轮进行重新分布,通过数值模拟对随机分布叶轮旋涡泵和均匀分布叶片旋涡泵的压力脉动特性进行分析和对比,并进行试验测试。
2 计算模型
2.1 模型建立与网格划分
本文研究对象为一台轴向旋涡泵,其结构包括叶轮及泵壳,其中泵壳又分为泵室和泵盖两部分,其三维造型如图1所示。叶轮外围由叶片分割为若干叶片槽,在泵室和泵盖内分别加工圆周沟槽作为流道,并均留阻隔面阻隔流体从泵的出口向进口泄漏。旋涡泵的主要几何参数如表1所示。

图1 旋涡泵三维造型

表1 参考旋涡泵的主要几何参数
对上述旋涡泵的三维流道模型进行造型,由于叶轮在运行时是轴向浮动的,假设叶轮处于泵腔的中间位置,即叶轮与泵室泵盖的轴向距离均为0.01mm。将泵内流体流道分为7部分,即进口流道、进口油膜、叶轮流道、平衡孔、出口油膜、径向间隙及出口流道,流道模型如图2所示。
流道模型的网格划分通过网格划分软件GAMBIT完成,由于旋涡泵内部流道复杂,对进口流道、出口流道及叶轮流道采用适应性强的四面体网格划分,对进、出口油膜、径向油膜及平衡孔采用扫略的网格划分六面体网格,划分网格如图3所示。
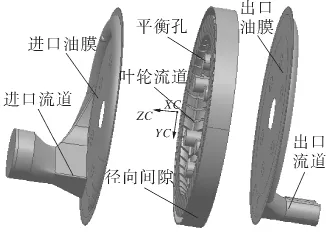
图2 旋涡泵内部流道模型

图3 旋涡泵计算流道及网格
2.2 计算模型与边界条件
旋涡泵内部流动较复杂,存在自由剪切湍流、附着边界层湍流及回流等流动形式,采用realizable k-ε模型进行湍流模拟;求解器的速度耦合方式采用SIMPLEC算法;在差分格式中,压力向采用标准格式,而速度项、湍动能项及湍动能耗散项采用二阶迎风格式。叶轮流道内的流体为转速5300 r/min的旋转体,其余为非旋转体。计算介质为gasoil-liquid。
非定常计算时,以定常模拟计算的计算结果作为非定常计算的初始条件,进口边界条件为给定质量流量,出口边界条件给定静压。取叶轮旋转2°所经过的时间6.28×10-5s作为时间步长进行计算。
考虑到泵内不同位置的压力脉动情况不同,在泵进出口油膜的轴向中间位置沿周向分别设置15个监测点,监测点分布如图4所示。除了在流体进入点及离开点各设置1个监测点外,从离开点开始每隔45°设置1个监测点,阻隔面的角度约为27°,则每隔9°设置一个监测点。
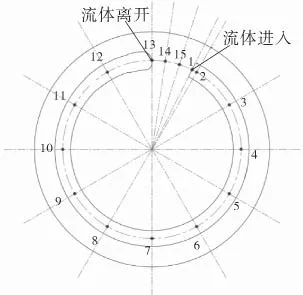
图4 监测点分布示意
3 压力脉动分析
3.1 均布叶片旋涡泵压力脉动特性分析
针对均布叶片旋涡泵的额定工况,对泵内部不同点的压力脉动情况进行分析和比较。从泵进口位置至泵出口位置依次取in2,in5,in7,in8,in10及in15点进行频谱分析和对比,傅里叶变换后的结果如图5所示。根据图5的计算结果可以看到,阻隔面内的监测点脉动幅值是最大的。整体来看,泵从进口到出口,各监测点的叶频脉动情况相当,而in2点由于其靠近进口,受流体运动影响较小,频率成分较为单一。随着监测点由进口向出口移动,由于受旋涡泵内部流体的湍流运动和旋涡的影响,除叶频外的附加的频率成分逐渐明显。在动静干涉与旋涡泵内部的旋涡运动共同作用下,阻隔面内的监测点in15的叶频幅值最大,且频谱图中的频率成分最为复杂。
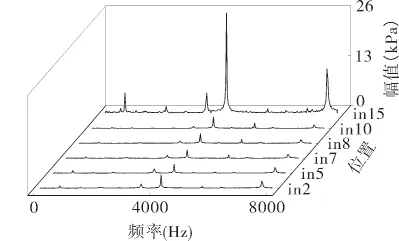
图5 不同位置监测点的频谱
由于叶轮与泵室泵盖阻隔面的动静干涉作用,在叶频处将产生较大的幅值,对各监测点在叶频处的幅值进行对比,如图6,7所示。
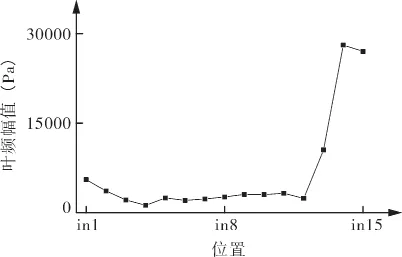
图6 进口侧各监测点叶频下幅值
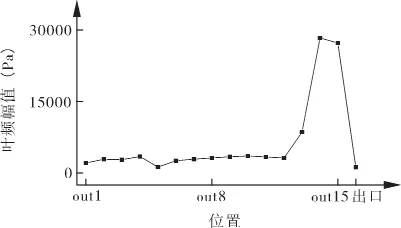
图7 出口侧各监测点叶频下幅值
根据图6,从in1点至in4点,叶频幅值逐渐下降。考虑到in1点至in4点区域为进口段的过渡区,该区域泵体流道截面积较大,对流体起到缓冲的作用,从而使该区域的叶频幅值有所下降。in4点后,直至动静干涉区前,各点的叶频幅值基本一致,当流体进入动静干涉区后,叶频幅值显著增大。
而出口流道侧各监测点的幅值变化情况与进口侧相近但略有不同。根据图7,流体同样在进入阻隔面区域后叶频幅值显著增大,且其幅值与进口侧叶频幅值相近,但在泵体出口侧流道区域内的out1点至out4点,该处流通截面较小,叶频幅值并没有入口侧叶频幅值的下降规律。
3.2 随机分布叶片旋涡泵性能和压力脉动特性分析
根据随机分布法则,对均布叶片进行了重新分布,设计了2种叶片分布方案,分布方案如表2和3所示。
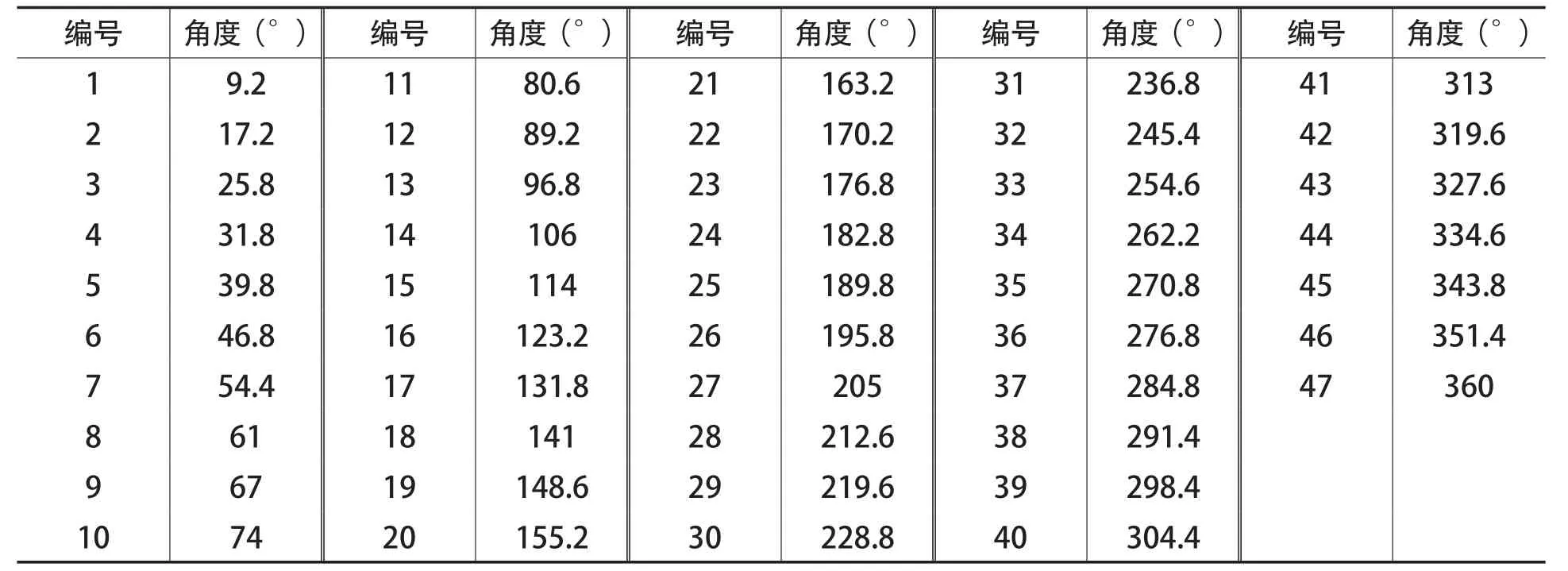
表2 随机分布方案一
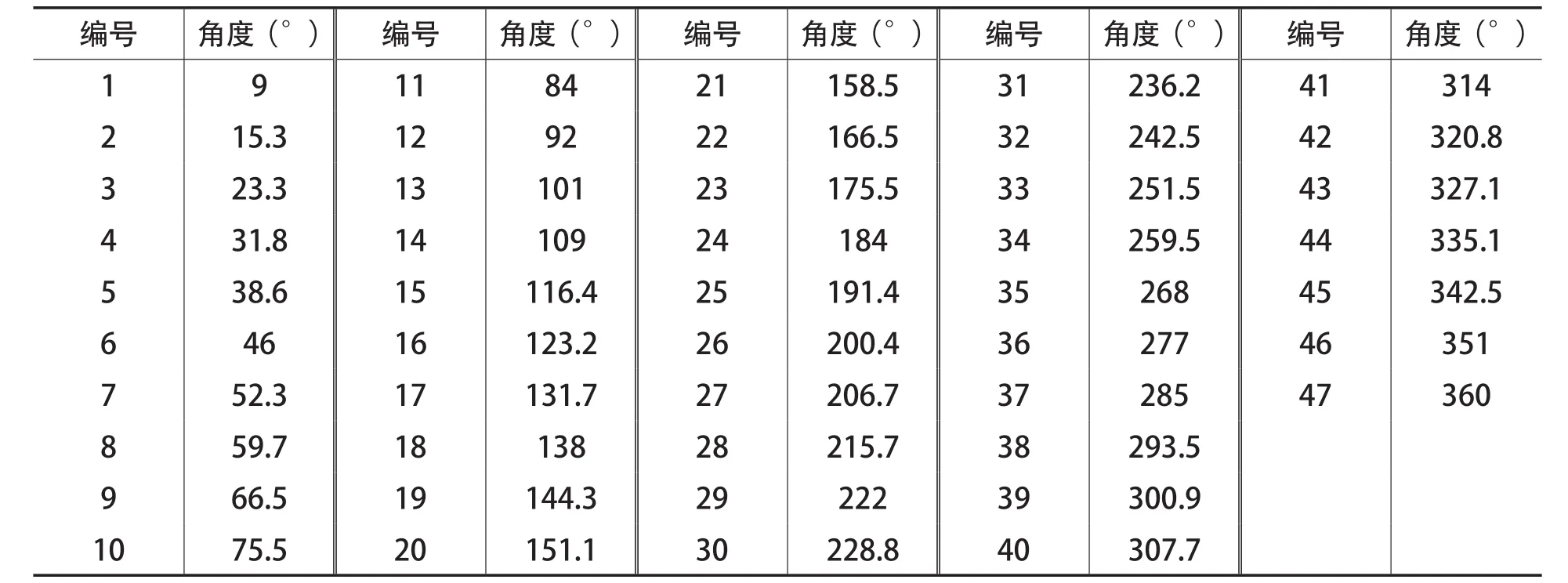
表3 随机分布方案二
对2个随机分布叶片旋涡泵模型的定常性能进行计算,并与均布叶片旋涡泵的性能进行对比,结果如图8和9所示。根据图8及图9的对比结果看出,3个模型泵的流量-扬程曲线相近;而3个模型的流量-效率曲线有一定的差别,随机分布方案二模型的效率要整体高于均匀分布模型和随机分布方案一,而其对应的性能曲线较为陡峭,而随机分布方案一的性能曲线最为平缓。由此,与均布叶片旋涡泵相比,非等距叶片分布法则并不显著影响旋涡泵的性能。
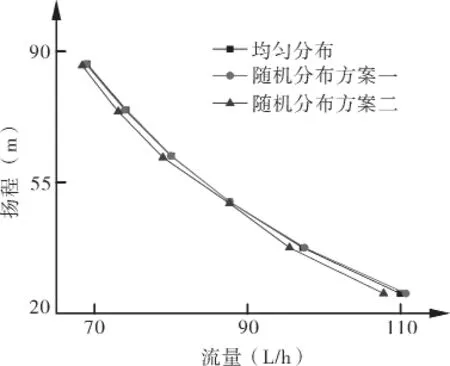
图8 3个模型的流量—扬程曲线
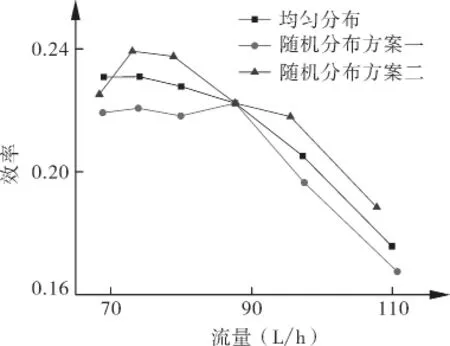
图9 3个模型的流量—效率曲线
对3个旋涡泵模型在工作工况点下的非定常性能进行计算、对比和分析。图10,11分别为随机分布方案一旋涡泵与随机分布方案二旋涡泵内部相同位置监测点下的频谱变化。将图10及11所示的in15点的频谱与均布叶片旋涡泵的监测点in15的频谱对比,可以看到经过叶片非等距分布后的旋涡泵最大幅值较均布叶片旋涡泵有显著降低,同时由于非等距分布,在叶频两侧产生了附加的频率成分,分散了叶频峰值强度,从而使旋涡泵的振动噪声总级明显降低。另外,从进口in2至出口in15,附加的频率成分呈增强的趋势。非均布分布使旋涡泵的内部流动更加复杂,从进口至出口,流体脉动受复杂流动的影响越来越大,导致附加的频率成分对应的幅值越来越大,叶频附近的频谱发生了叠加。
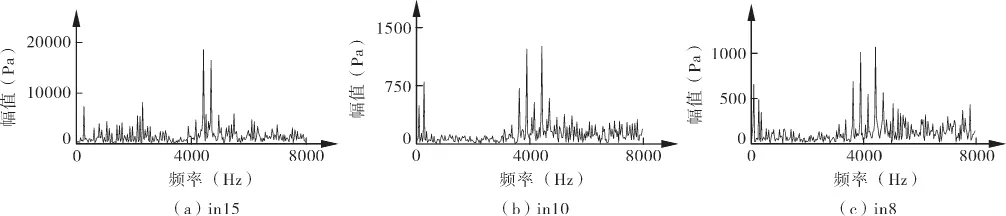
图10 随机分布方案一不同监测点的脉动频谱
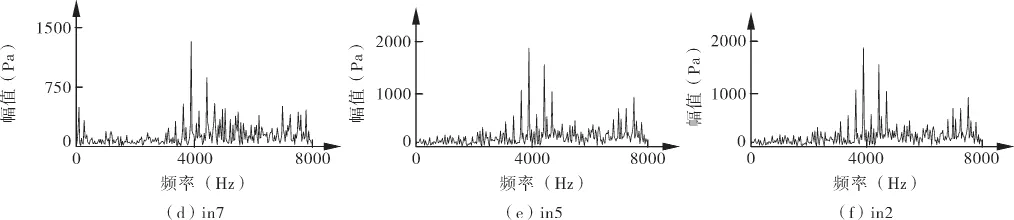
图11 随机分布方案二不同监测点的脉动频谱
3.3 压力脉动振动试验测试
由于所研究泵的尺寸小,结构紧凑,泵的叶片通过频率超过4000 Hz,该频率衰减很快,难以直接测量流体脉动。考虑到泵内部流体的压力脉动将通过流体诱导泵体振动的方式传输到外部装置上,并引发振动,故通过泵体振动测试的方法进一步分析旋涡泵的压力脉动特性。
泵振动测试的的具体过程为:将振动加速度传感器贴于泵芯外壁,传感器位置位于旋涡泵吸入口附近。等距分布旋涡泵测试结果和CFD计算结果如图12,13所示。由图12和13的试验与数值模拟的对比结果可以看到,CFD模拟得到的压力脉动频谱特性与旋涡泵振动频谱在趋势上具有一致性。整体上看,叶频仍是振动的主要频率,叶频处的振动幅值最大。
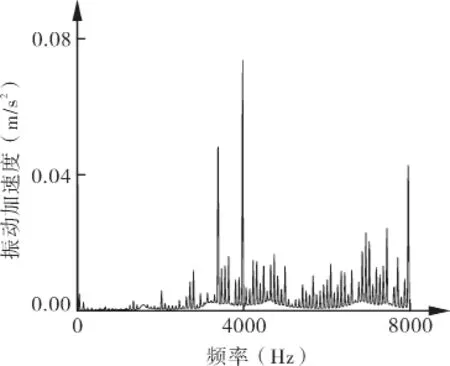
图12 等距分布旋涡泵振动测试频谱分析
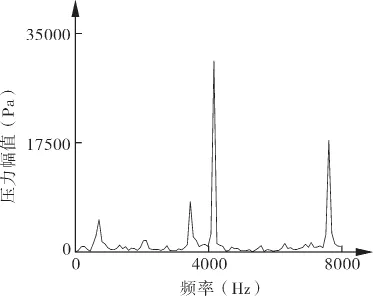
图13 等距分布旋涡泵模拟计算频谱分析
更进一步,按照随机分布方案一加工非均布叶片叶轮并进行振动测试,分析结果如图14所示。
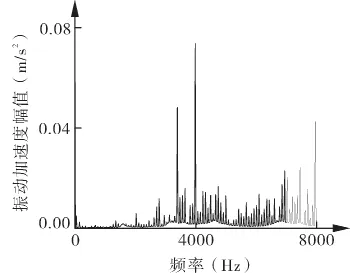
图14 随机分布方案一的泵芯外壁振动频谱
对比图12和14的振动测试频谱图可以得到,对于均布叶片旋涡泵,叶频位置有明显的尖峰,对于非均布叶片旋涡泵,叶频处的峰值显著降低,叶频两侧有明显的附加频谱。试验结果与数值模拟结果一致,同样表现出非均布叶片分布旋涡泵较均布叶片分布旋涡泵的叶频峰值低,且产生附加频率,频谱更均匀,说明泵内压力脉动是旋涡泵的主要振动源。
4 结论
(1)由旋涡泵的叶轮与静止部件动静干涉引起的叶频是旋涡泵压力脉动的主要组成频率,且在阻隔面附近叶频的幅值最大。旋涡泵内部流体的湍流运动和旋涡还会引起其他频率成分的压力脉动,但幅值较小。
(2)随机分布叶片旋涡泵能显著降低在叶频处的脉动峰值,但由于其内部流场更为复杂,在叶频两侧产生了附加的频率成分,而振动噪声总级上有明显下降。
(3)对于叶片等距和非等距分布的旋涡泵,CFD模拟得到的压力脉动频谱特性与旋涡泵振动频谱在趋势上具有一致性,说明泵内压力脉动是旋涡泵的主要振动源。
[1] Engeda A,Raheel M M. Systematic design approach for radial blade regenerative turbomachines[J].Journal of propulsion and power,2005,21(5):884-892.
[2] Song J W,Engeda A,Chung M K. A modified theory for the flow mechanism in a regenerative flow pump[J]. Proceedings of the Institution of Mechanical Engineers,Part A:Journal of Power and Energy,2003,217(3):311-321.
[3] Quail F J,Stickland M,Baumgartner A. A onedimensional numerical model for the momentum exchange in regenerative pumps[J]. Journal of Engineering for Gas Turbines and Power,2011,133(9):093001.
[4] Quail F J,Scanlon T,Baumgartner A. Design study of a regenerative pump using one-dimensional and threedimensional numerical techniques[J]. European Journal of Mechanics-B/Fluids,2012,31:181-187.
[5] Francis J Quail,Thomas Scanlon,Matthew Strickland.Development of regenerative pump impeller using rapid manufacturing techniques[J]. Rapid Prototyping Journal,2010,5(16):337-344.
[6] 王洋,傅剑辉,蒋其松. 闭式叶轮叶片位置对旋涡泵性能的影响[J]. 农机化研究,2010,32(9):150-154.
[7] 沙毅,李金磊,刘祥松,等. 自吸旋涡泵变转速性能与内部流场试验[J]. 农业机械学报,2009 (12):119-124.
[8] 张菲茜,武鹏,吴大转,等. 微型旋涡泵水力特性计算与轴向力研究[J]. 排灌机械工程学报,2014,32(8):658-662.
[9] Yanagihara N,Murakami T,Shiraishi H,et al,Noise reduction of a regenerative pump[J]. Transactions of the Japan Society of Mechanical Engineers Series B,1993,59(565):2863-2867.
[10] 表寿其,薛菲,袁建平,等.离心泵压力脉动对流动噪声影响的试验研究[J].排灌机械,2009,27(5):287-290.
[11] 河合勇太,本田义彦 . 流体泵:CN 102062104[P].2011-05-18.
[12] 武鹏,张菲茜,吴大转,等. 非等距叶片微型旋涡泵压力脉动特性研究[J]. 工程热物理学报,2015(4):775-779.

