基于圆渐开线涡旋膨胀机几何模型的研究

彭 斌，李要红，赵生显，朱永军，张朋成

（兰州理工大学，甘肃兰州 730050）

1 前言

对于涡旋机械原理的研究，最早是由法国工程师Leon Creux提出［1］，并在1905年于美国取得专利。但由于当时其优势并未被发掘以及技术的限制，涡旋机械没有得到深入发展。直到20世纪80年代涡旋压缩机才得以广泛研究，而涡旋膨胀机则是由涡旋压缩机改装而来。经相关资料显示，涡旋膨胀机最早是由日本某汽车生产公司用于rankine中，作为回收余热装置，以提高发动机的效率，得出回收的能量约占机车输出总能量的3%［2］。近年来，由于资源的短缺、环境问题的日益加重，涡旋机械的研究已得到国内外各研究机构的重视。作为回收余热装置关键部件的涡旋式膨胀机，因其结构紧凑、体积较小、可靠性好、振动小和容积效率高等优点得到广泛的使用。涡旋膨胀机性能的研究更是成为国内外研究的热点。为了分析涡旋膨胀机整机的性能，其几何模型的研究是基础。关于涡旋膨胀机的研究，主要集中在对其热力学、动力学和泄漏方面的分析，实际上，对其几何模型的研究也是较为重要的。

由于涡旋膨胀机是由涡旋压缩机改装而来，因此，涡旋膨胀机的几何模型与涡旋压缩机几何模型极其相似。Morishita第一次对涡旋压缩机几何和动力学模型进行了详细的论述［3］。型线的构成结构对涡旋压缩机的性能影响较大，型线主要有圆渐开线、线段渐开线和正多边形渐开线等，目前常用的渐开线为圆渐开线。由于加工型线时干涉的存在，使得齿头形成尖角，这会产生很大的应力，在高温高压下容易损坏；涡旋线始端刚性降低，使变形增大，磨损加快，而且加工时难以保证加工精度，因此对型线始端的修正也是必不可少的。对于型线始端的修正，也做了大量的研究。王君等通过双圆弧修正的方式，得出圆渐开线型线双圆弧修正的生成方法［4］。文献［5～7］通过双圆弧修正以及对称双圆弧加直线修正，得出压缩腔面积直接影响压缩过程中气体的压力、温度变化和最终的压缩比，中心腔的面积影响排气口的速度和压力变化。

本文以圆渐开线为型线对涡旋膨胀机的几何模型展开研究。以双圆弧修正为基础，得出双圆弧加直线修正后膨胀机的吸气容积，为膨胀机动力学、热力学模型做好基础。

2 圆渐开线以及型线的生成

一条直线与半径为rb的圆相切，直线绕圆转动，直线上某一点的轨迹即为圆的渐开线，该圆则称为基圆。如图1所示，以φ为参数建立坐标系，由几何关系可求得渐开线上一点的坐标M（x，y），φ为与M点相对应的渐开角，于是渐开线的方程可写为：

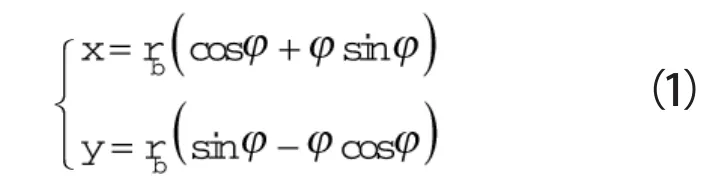
式中 rb——基圆半径

为计算方便，假设内外壁型线的渐开线起始角相等，取为α。进而可求得涡旋膨胀机内外壁型线的方程：

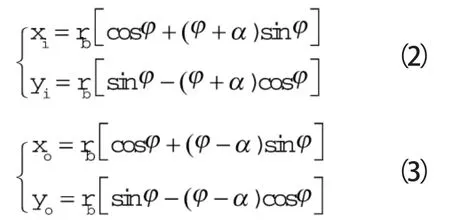
式中 α——内外壁渐开线起始角i，o——下标，内、外壁线

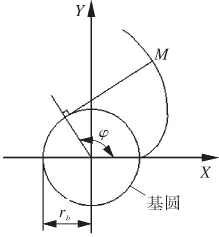
图1 圆渐开线生成

图2所示为壁厚为t的静涡旋盘型线。动涡盘由静涡盘旋转180°得来，因此动静涡盘型线相同。

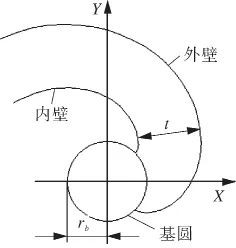
图2 静涡盘示意

3 涡旋型线修正

常见的涡旋修正型线有双圆弧修正、圆弧加直线修正、多对圆弧修正、三角函数修正和二次曲线修正等。为了满足涡旋膨胀机涡旋齿齿头的刚度，一般采用双圆弧加直线修正。

3.1 双圆弧加直线修正

为了避免由刀具干涉导致齿头形成尖角，修正是必不可少的。强建国等人采用等角双圆弧加直线的修正方法，推导出修正之后齿头增加的面积计算方法［8］，但过于复杂。如图 3（a）所示为双圆弧加直线修正示意。图中，φ为修正角，Oo、Of分别为动静涡盘基圆中心，O2和O1为修正圆弧的圆心，l为修正直线的长度，θ＊为开始膨胀角。首先给出修正角φ，可得点C和点D的坐标，通过C、D两点做基圆切线，交于内外壁线A和B，过基圆圆心与X轴成γ角的直线分别与直线AD、CB交于点O2和O1，O2、O1即为两修正圆弧的圆心。分别以AO2和O1B为半径做圆，最后做出两圆的内切线（即修正直线EF），由涡旋齿的啮合得到图 3（b）。

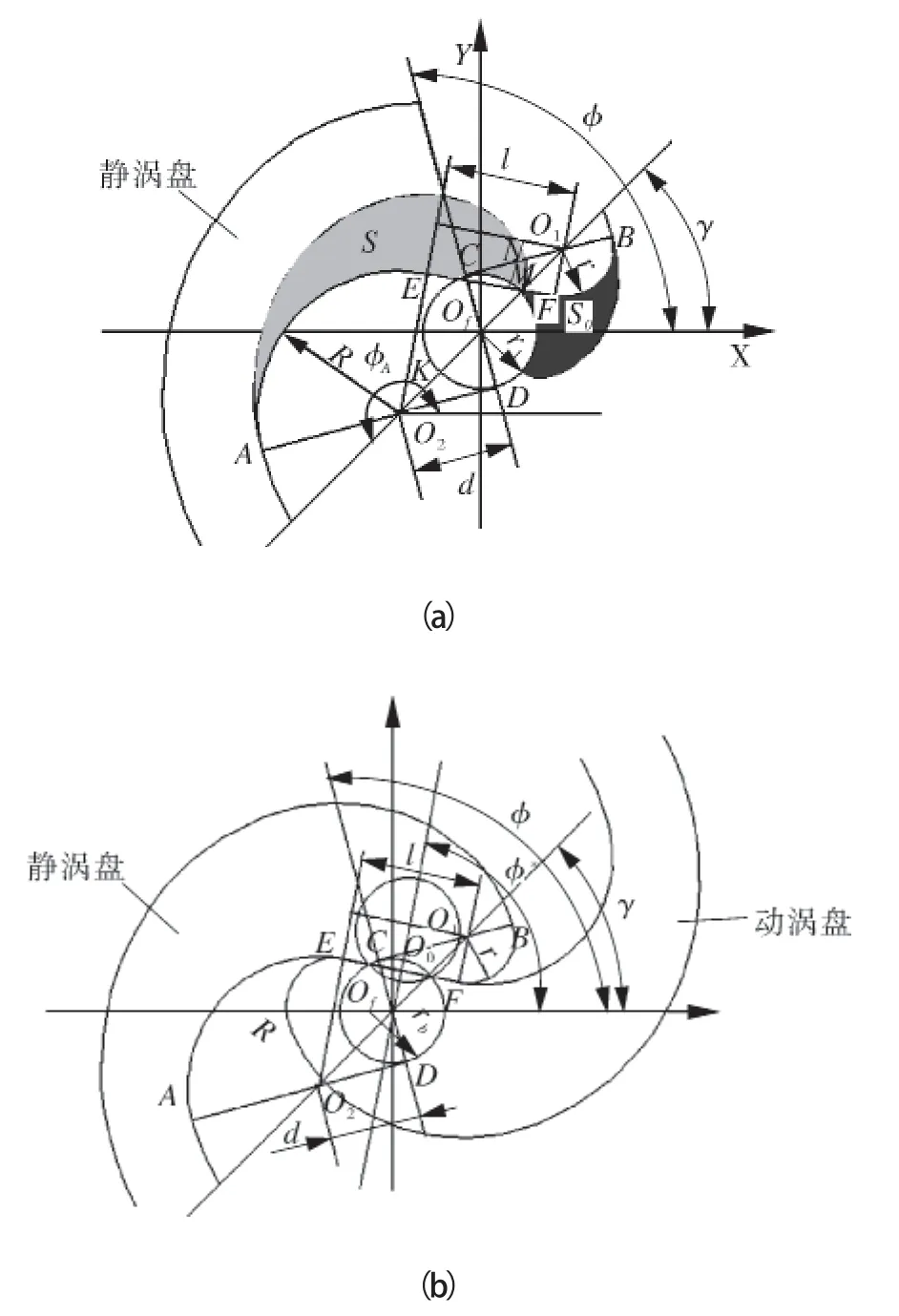
图3 双圆弧加直线修正

图中几何关系由下式表示：

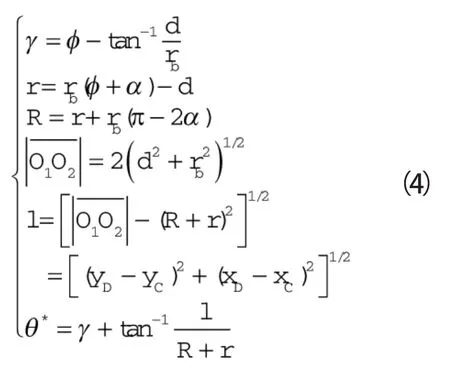
根据文献［8］，可求得E、F的坐标为：

3.2 修正后增加的壁厚面积

修正后涡旋壁厚所增加的面积，即为如图3（a）所示阴影部分的面积。其具体求解方法为：

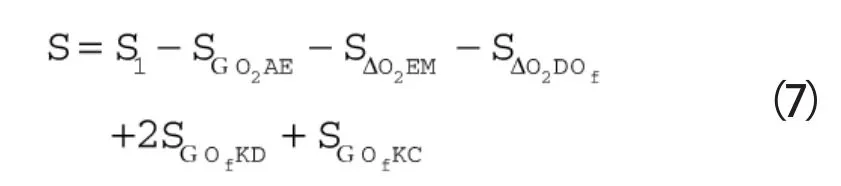
其中，S1为内壁型线从发生角α到A点时的发生角φA所形成的面积，由圆渐开线的展开特性可知该部分面积的计算方法为：

式（7）中各扇形和三角形的面积可由几何关系得到，文中不做详细的推导。

3.3 修正参数对吸气容积的影响

涡旋膨胀机吸气容积的大小，主要和涡旋齿始端型线的修正有关，而双圆弧加直线修正型线主要是由起始修正角γ和修正角φ决定。在假定起始修正角 γ 不变的情况下（本文取γ=110°），通过改变修正角φ的大小，并结合式（4）～（6）计算出修正所用其他的参数，从而计算出修正之后涡旋齿始端的投影面积，最后计算出涡旋膨胀机吸气容积的大小变化。

图4所示为起始修正角γ=110°时修正型线随修正角φ的变化，表1为主轴转角 θ=90°时修正参数的变化及吸气容积的变化参数，从图4和表1中可以看出，在起始修正角一定的情况下，随着修正角的增大，涡旋膨胀机吸气容积增大，增大修正角能增加涡旋膨胀机的吸气容积，进而增大膨胀比。当φ=41.5°时，齿头始端形成尖角，容易造成应力集中，应当避免；当φ=52°时，修正变为双圆弧修正。因此修正角的取值范围为41°≤φ≤52°。

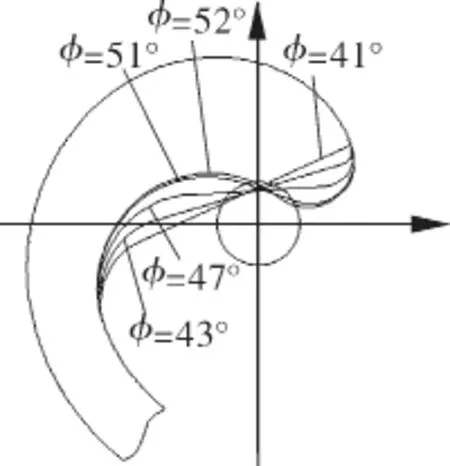
图4 修正型线随φ的变化

表1 修正参数及各吸气容积

4 涡旋膨胀机几何模型

4.1 涡旋膨胀机工作原理

涡旋膨胀机经吸气、膨胀、排气3个工作过程，由高温高压的有机工质带动动涡盘做功，将气体的内能转化为机械能输出。其涡旋齿啮合过程如图5所示。

图5 膨胀机工作过程

此处规定涡旋膨胀机主轴转角θ=θ＊时膨胀机开始吸气，主轴转角θ=2π+θ＊时吸气结束，θ＊为开始膨胀角，动涡盘齿头与静涡盘内壁面啮合，开始膨胀。直到主轴转角θ=θd时，进入排气阶段，开始排气。即进入的一团气从吸气、膨胀、排气完成一次工作过程。θd为开始排气角，也叫膨胀结束角。

4.2 未修正工作腔容积计算

对于圆渐开线作为型线的涡旋膨胀机工作腔容积的计算，目前有2种计算方法，一种是根据圆渐开线的展开特性，通过积分直接计算出工作腔容积的解析计算公式［11］，从而得出其月牙形腔轴向投影面积；另一种是根据法向等距法，将封闭月牙形工作腔的轴向投影面积等价为相互啮合的两型线组成的等宽度环槽面积，通过计算等宽度环槽中心型线的长度与公转半径的乘积，得到工作腔容积［12，13］。

本文采用Morishita在假定内外壁线渐开角相等的情况下，推导出的压缩过程和排气过程工作腔容积表达式［3］。未修正时涡旋齿的啮合如图6所示，从图中可以看出，各腔体V1～V3、Vd的划分以及各啮合点1～4，图中 θ 为主轴转角。当θ=θ＊时，吸气腔开始吸气，随着主轴转角的增大，吸气容积增大，至θ=2π+θ＊时即吸气结束，开始膨胀。当主轴转角θ=θd时，膨胀结束由于在开始排气时继续膨胀，因此体积继续增大，随着主轴转角的继续增大，进入排气过程，气体体积减小。

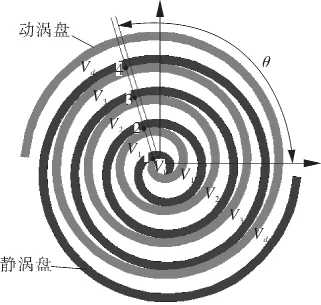
图6 未修正型线啮合

吸气腔容积V0的计算与涡旋压缩机排气腔体积的计算类似，其计算方法为：

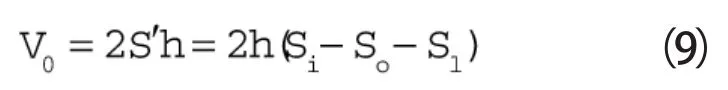
h——涡旋体高度

Si——涡旋盘内壁面型线形成的面积

So——涡旋体壁厚部分投影面积

Sl——两基圆之间围成的面积

各面积计算方法如下：

以第一膨胀腔V1为例，计算由啮合点1和啮合点2所形成月牙腔容积：

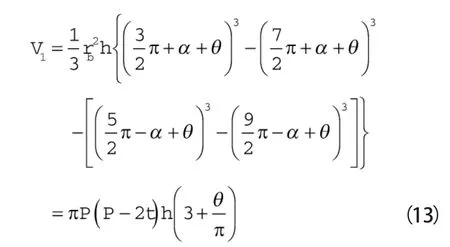
式中 P——涡旋体节距

t——涡旋体壁厚

则第i（i≥1）个膨胀腔的容积为：

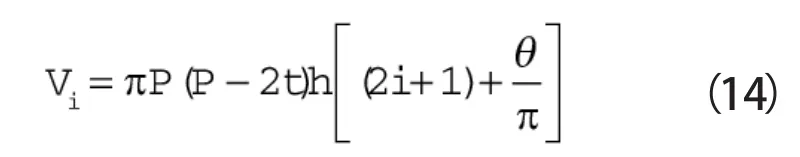
排气腔的容积为：

式中 r0——回转半径

4.3 修正后工作腔容积计算

如图3（a）所示，阴影部分S的面积为修正之后涡旋体壁厚所增加的面积。So为修正涡旋体壁厚所减少的面积。文献［9］对修正后的工作腔容积计算做了详细的推导。实际上，从图3可以看出，齿端的修正只对膨胀机的开始膨胀角θ＊有影响，其吸气的过程与未修正之前一样，忽略修正对壁厚中心线的影响，则对于修正后工作腔容积的计算方法可近似与未修正之前一样，只是在吸气过程中，吸气容积总体减小2（S-So）h。其中S由式（7）求得，So的求解方法为：

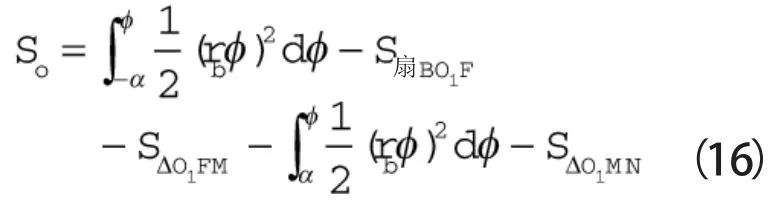
5 泄漏

对涡旋膨胀机热力学的研究，泄漏线的长度以及泄漏面积的计算是必不可少的。涡旋压缩机的泄漏有切向泄漏和径向泄漏2种。Halm给出了2种泄漏的计算方法，但是没有考虑泄漏线是控制容积的哪一侧［13］。Chen分别对控制容积两侧的泄漏线给出了不同的计算方法［14］。

5.1 切向泄漏

由于存在径向间隙，会产生切向泄漏，其途径包括吸气腔与膨胀腔、膨胀腔与膨胀腔、膨胀腔与排气腔之间的泄漏。切向泄漏线的长度为涡旋型线的高度，其泄漏面积的计算方式为：

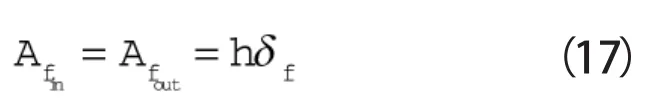
5.2 径向泄漏

动静涡盘在装配时存在轴向间隙，产生径向泄漏。涡旋膨胀机的径向泄漏是高压腔体中的工质气体通过轴向间隙流向低压腔体。本文假设每一对月牙腔内气体的压强分布均匀，即不考虑一对腔体之间存在的泄漏。则径向泄漏由两部分组成，即由上一腔体的泄入和向下一腔体的泄出。如图7所示为涡旋膨胀机径向泄漏示意。

图7 径向泄漏示意

如图所示，由上一腔体泄入的泄漏线长度是动涡旋齿外壁型线的长度，由圆渐开线的几何关系可知，膨胀机工作腔径向泄漏由上一腔体泄漏进来。泄漏线长度及泄漏面积计算公式为：

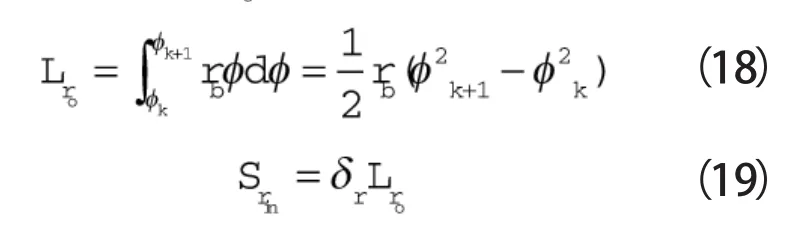
φk，φm—— 动静涡盘啮合点处涡旋齿型线的渐开角

向下一腔体泄出的泄漏线长度是静涡旋盘内壁型线的长度。月牙腔向下一腔体的泄漏线长度及泄漏面积为：

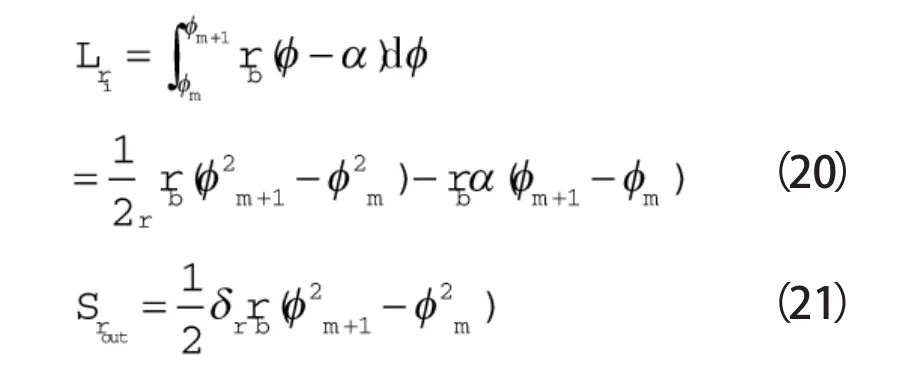
δf，δr—— 切向间隙和径向间隙，一般与吸气压力和排气压力的比值有关δf和δr由以下两式求得［15］：

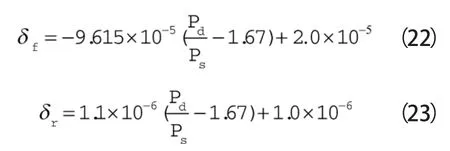
当对圆的渐开线最初一段进行修正时，会影响到单位宽度渐开线的中心线长度（涡旋体壁厚中心线），即处于吸气腔内的径向泄漏线长度的计算。但为了便与计算，以及从工程应用的角度出发，可以忽略型线齿端修正所造成的径向泄漏线长度变化量。

6 算例与分析

本文采用MATLAB软件，对涡旋膨胀机的容积变化进行编程计算，涡旋膨胀机的具体参数见表2。图8，9分别为涡旋齿未修正时，涡旋膨胀机容积变化曲线以及容积变化率。

表2 涡旋膨胀机几何参数

图8 容积变化曲线

图8中，随着主轴转角的增大，膨胀机各工作腔容积逐渐增大。吸气结束后进入膨胀过程，主轴转角继续增大，到膨胀结束开始排气。由于排气口的节流作用，使得排气腔容积继续增大，达到最大值后容积逐渐减小，完成吸气、膨胀和排气过程。图9为各腔容积变化率曲线，吸气腔容积变化率增大，膨胀腔增速不变，排气腔总体呈负增长趋势。

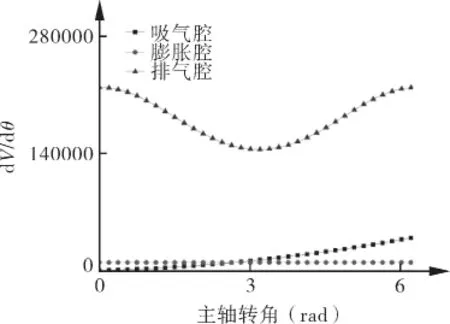
图9 容积变化率

图10（a）所示为未修正和双圆弧加直线修正的吸气腔容积变化对比，图10（b）为主轴转角θ=90°时膨胀机吸气容积随修正角的变化规律。从图中可以看出，膨胀机吸气容积随着修正角的增大而增大，因此，通过增大修正角，可以增大膨胀机的吸气容积，从而改变膨胀比，提高膨胀机的效率。

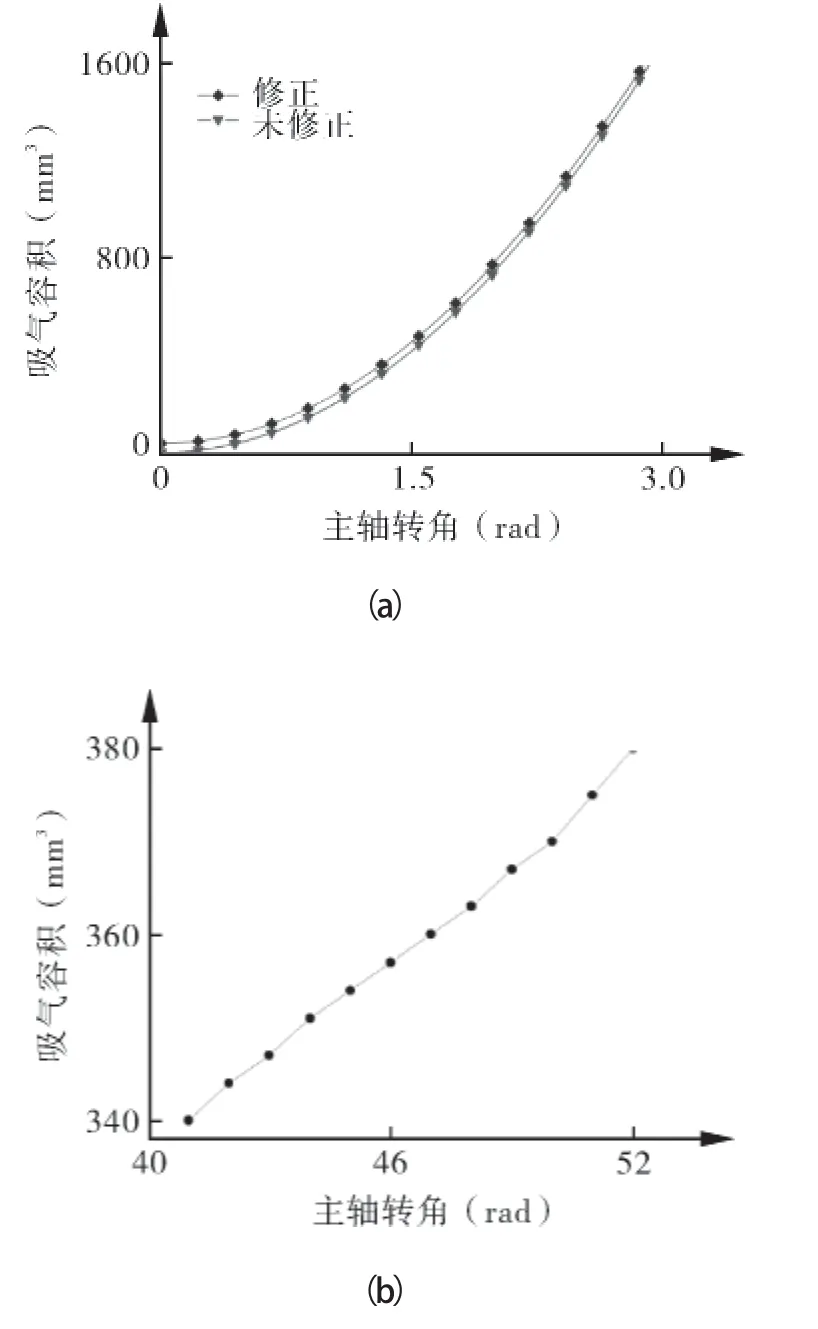
图10 修正吸气腔容积

图11所示为涡旋膨胀机月牙腔径向泄漏线长度随主轴转角的变化曲线。随着主轴转角的增大，径向泄漏线长度不断增加。从图7可以看出，在计算吸气腔与第一膨胀腔之间的泄漏线时，动涡盘的外壁型线和静涡盘内壁型线之间存在一定的角度差，所以曲线最初一段会出现一微小突变。当膨胀机开始排气时，第四膨胀腔与排气腔接通，不再有泄漏线，因此曲线末端则变为零。

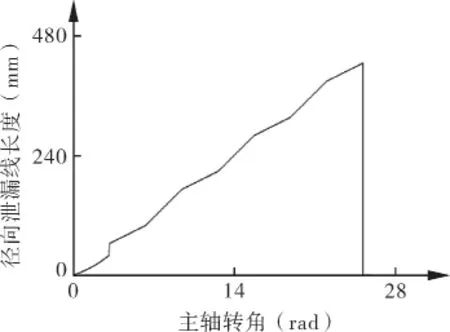
图11 径向泄漏线长度变化

7 结论

（1）本文以圆渐开线为涡旋型线为基础，对涡旋齿齿端的修正展开讨论，并对双圆弧加直线修正做了详细论述，给出其所增加壁厚的计算方法。

（2）对膨胀机工作过程和工作原理，以及各腔体的划分做出分析。

（3）用积分法，对未修正以及双圆弧加直线修正后涡旋膨胀机容积进行计算，使用MATLAB编程得出容积变化和变化率曲线，并对两者进行简单的对比分析，得出修正对膨胀机容积的变化比较小，通过增大修正角，可以增大膨胀机的吸气容积。

（4）对膨胀机工作腔的泄漏做简单的分析与探讨，给出泄漏线长度和泄漏面积的计算方法，并做出膨胀机月牙腔径向泄漏线长度变化曲线，得出径向泄漏线的长度随主轴转角的增大而增加。

［1］ Creux L.Rotary engine［P］. US Patent No 801182，1905.

［2］ Society of Automotive Engineers.New engine design and engine component technolygy［M］. Society of Automotive Engineers（SAE），1993.

［3］ Morishita，Sugihara E M. Scroll compressor analytical model［C］. 1984 International Compressor Engineering Conference at Purdue University，1984：487-495.

［5］ 高秀峰，冯诗愚，顾兆林，等. 对称圆弧修正齿型涡旋压缩机排气孔的开设分析［J］. 西安交通大学学报，2000，34（6）：89-92.

［6］ 李连生，束鹏程. 涡旋型线对排气口侵入及排气流速的分析计算［J］. 西安交通大学学报，2000，32（7）：56-59.

［7］ 高秀峰，郁永章.对称修正齿涡旋压缩机排气研究［J］.压缩机技术，1999，157（5）：3-7.

［8］ 强建国，刘振全. EA-SAL修正涡旋齿端面积计算［J］. 兰州理工大学学报，2006，32（5）：36-39.

［9］ Wang，Li B，Shi X，et al. A general ge- ometrical model of scroll compressors based on discretional initial angles of involute［J］.Int. J. Refrig.，2005（28）：958-966.［10］ 刘涛，邬再新，刘振全. 法向等距线法生成涡旋压缩机型线的研究［J］. 机械工程学报，2004，40（6）：55-58.

［11］ 王君，李雪琴. 多齿涡旋机械啮合型线的构建理论［J］. 机械工程学报，2008，44（4）：74-79.

［12］ 顾兆琳，郁永章，冯诗愚. 涡旋压缩机及其它涡旋机械［M］. 西安：陕西科学技术出版社，1998.

［13］ Halm N P. Mathematical model of scroll compressor［D］. MasterThesis，Purdue University，1997.

［14］ Chen Yu. Mathematical modeling of scroll compressors［D］. MasterThesis，Purdue University，2004.