基于社会计算的大数据集关联规则的研究

马宪敏

(黑龙江外国语学院 信息工程系， 哈尔滨 150025)

0 引言

在社会计算方面，需要提供认为最适合用户当前场景的某种服务[1]。本文研究从大量用户数据中提取出规则。近年来，社会计算受到广泛应用，包括医疗保健系统和智能车辆系统均是这方面的应用典范。实施过程中，关键一点在于从大数据中准确、快速地提取有用规则，并高效地处理用户所处环境以便为用户提供最好的服务[2]。

实践中，社会计算系统往往需要满足实时性。因此，重要的是通过应用可简化关联规则数目的方案减少运算数据量；从而缩短数据处理时间。规则简化方案保证数据完整性和较高的时间效率，为现实环境中部署社会计算提供了关键因素[3]。

规格简化方案所适用的数据很特别地存在二进制属性。先后有人提出了利用数据二进制属性来挖掘关联规则的各种算法，如直接散列，修剪，划分法和动态项目集计数法。这些方法普遍用来增强挖掘效果，减少数据库扫描次数及降低候选数据集数目。此外，有人提出了利用属性分类或用户属性约束来挖掘广义关联规则的方法；通过借助于直方图和样本，找到不相关项目来挖掘负关联规则的技术。对目标数据的关联性进行分析所采用的基础方法，其目的在于找出交易中频繁出现的次数高于下限值的项目。由于所采用的数据结构较简单，且结果存在确定性，故基于频率的方法已得到广泛应用。但是，随着项目数不断增多，计算时间急速增加，提取不频繁出现的数据规则方面的信息就变得困难[4-5]。

为克服已有算法对大数据关联规则挖掘存在的弊端，本文提出以二进制数字形式来表示数据集，对每个项目分配一个权重的WTabular算法。而且，利用奎因-麦克拉斯基算法[6]将逻辑函数简化成一个算法。本文算法可减少不必要的规则，改善关联规则的挖掘效率。实验表明，无论是实用性和有效性还是规则简化率和处理时间，本文算法较APRIORI算法[7]和FP增长算法[8]这两种代表性算法均表现更佳。本文算法更适用于要求对大数据及时处理的社会计算领域。

1 相关研究工作

关联规则是许多交易进行累积后交易与数据库之间关联性挖掘过程的结果；通过统计方法可以找到存在关联的项目之间的规则性。例如，它们之间存在关联：“如果发生了事故，其他事故也会发生”。

通过搜集大量交易，一个项目集与另一个项目集之间的关联可以提取到，表明它们之间存在相似性或一个模式。关联规则的基本特性是：对于一组交易表示为I，如果非空集合X和Y满足XI和YI，表明当事故X发生后，事故Y也会发生。

规则的关联等级由支持度和置信度来衡量。给定两个数据集A和B，支持度S决定一条规则如何频繁应用到给定的数据集；置信度C决定隶属于B的项目在A中出现的次数。这两个指标分别定义，如式(1)、(2)。

支持度：

(1)

置信度：

(2)

其中，σ(A)表示A含有的项目个数；支持度用来衡量关联规则的有用性。一个非常低的“支持”的规则可以被判断为偶尔发生，因此很难说这条规则是有用的。置信度衡量一个规则推理的有效性，

可以说给定规则A→B的可靠性越高，B在A中出现的概率就越大。因此，置信度界定B对A的条件概率。

从数据库找到关联规则分两步：(1)寻找频繁项；(2)生成关联规则。

步骤1: 寻找频繁项

频繁项的最大数即项目集的幂集的大小。如果用户感兴趣的项目个数增加，项目集也呈几何级数增长。扫描数据库，计算每个项目的支持度，从而找到频繁项。

步骤2: 生成关联规则

1.1 APRIORI算法

APRIORI算法应用于候选项目。首先计算每个候选项目的频率[8]；再根据数据集的最小支持度确定频繁项；算法过程如下：

APRIORI算法

L1={Large-itemsets};

For(k=2;Lk-1=0;k++) do begin;

Ck=Apriori-gen(Lk-1);

For all transactionst∈Ddo begin;

Ct=subset(Ck,t);

For all candidatesc∈Ctdo

c.count++;

End

Lk={c∈Ct|c.count≥minsup};

End;

首先，生成包含了候选频繁项C1；然后，对属于C1的每个候选频繁项的数据库进行扫描；计算每个元素的支持度值；接下来，选出支持度值满足置信度要求的项目，作为一个集合L1；对两个元素的各子集进行上述操作；因为每个子集的元素个数会逐个增加，该过程需重复下去，直至不再有满足要求的元素出现。

APRIORI算法生成由支持度大于最小置信度的项目构成的候选项目集；从而缩小搜索空间。但是，随着满足最小支持度的项目数量增多，会有大量要求重复扫描数据库的候选集产生。要生成候选集，所有项目集的幂集生成为候选集且候选集的每个元素的频率通过扫描数据库可得到。这么做会导致产生并不存在的项目，充当交易数据里的候选集，浪费时间和空间。

1.2 FP树算法

另一个将与本文算法对比的FP增长算法将含有频繁项的数据库压缩成FP树，生成条件模式树，采用分而治之方法对与每个项目关联的树进行挖掘，同时挖掘关联规则。

给定一个FP树R，按照支持度升序方式对R里的每个频繁项构建随后的FP树。[9]找出树里频繁项的所有出现次数；对每次出现，确定到达根部的路径。记录下每条路径上项目的支持度值；将该路径插入新构建的树Rx，其中X是对项目加以前缀P后获取到的项目集。插入路径时，Rx上每个节点的权重随着项目-i的路径支持度pathsup(i)而增长；之后，递归调用FP增长函数，Rx与X作为参数。当输入FP树是单路径时，存在一个基本情况：穷举路径子集的所有项目集来处理单路径FP树，以这样的项目集的支持度值作为其中的最小频繁项。

由于FP增长算法不生成候选集，也不共享频繁集，所以比APRIORI算法浪费空间较小。它在速度方面也很出色，因为数据库扫描只进行两次。不过，FP增长算法要求对树结构进行压缩以对关联规则进行快速挖掘，导致新数据添加困难。

1.3 奎因-麦克拉斯基算法

奎因-麦克拉斯基算法使布尔函数最小化。功能上它与卡诺映射大同小异，只是其制表形式效率高，所以经常作为作计算机算法。该算法采用一种确定性方式来检查布尔函数是否达到极小形式。有时可称为制表法。此法分两步：

1. 寻找函数的所有主蕴含项

2. 从主蕴含项图表里，找到函数的必要主蕴含项

例如，假设减少方程的功能如式(3)。

f(A,B,C,D)=∑(4,8,9,10,11,12,14,15)

(3)

通过对最小项求和，可以形成式(4)乘积和正准表现式。

fA,B,C,D=A′BC′D′+AB′C′D′+AB′C′D+AB′CD′+AB′CD+ABC′D′+ABCD′+ABCD

(4)

式(4)不是最小的。为了使函数最小化，将所有评估成1的最小项首先以最小项形式按表格排列，然后与其他最小项合并。如果两个项目相差只有一个单位数，用连接符“-”取代它，表明它无足轻重。

继续操作直至不再有项目可以合并，至此创建主要的主蕴含项表格。

2 本文研究方法

本文提出一种新的挖掘方法，它有效减少大数据的关联规则数目，同时具有较高的置信度和支持度。从大规模数据库的数据里找到置信度高的规则，是包括社会化计算在内诸多领域里的一项非常重要的工作，其中主要涉及对大数据的高效处理问题。因此，本文提出WTabular算法，它以二进制数字形式来表现交易数据集；通过与奎因-麦克拉斯基法和权重分配法结合，提高了关联规则的挖掘效率。

2.1 基本运算

本文提出的WTabular算法以二进制数字形式表达数据集以及将权重与奎因-麦克拉斯基法相结合来简化挖掘过程，有效改善了数据挖掘的效率。该过程由两部分构成：(1)预处理：分3步；(2)后处理：分4步。前3步预处理环节去除叠加或不必要的数据并将数据转化为适合分析的格式；具体步骤如下：

步骤1：先行部分的规则由小到大依次按1进行排列；

步骤2：从数据库的规则里，找出先行部分之后部分的值为1的规则；

步骤3：计算步骤2找到的规则的权重；剔除权重值小于预设值的那些规则；

步骤4：通过预处理方式生成的数据相互比较，然后再进行简化；

步骤5：通过比较数目1为i及i+1的项目将其进行简化；

步骤6：重复步骤4和5步对初次简化的结果进一步简化； 如果没有更多的减少是可能的，就停止工作；

步骤7：删除重叠的规则。

2.2 分配权重到关联规则

随机生成的数据集用来解释文中算法，如表1所示。

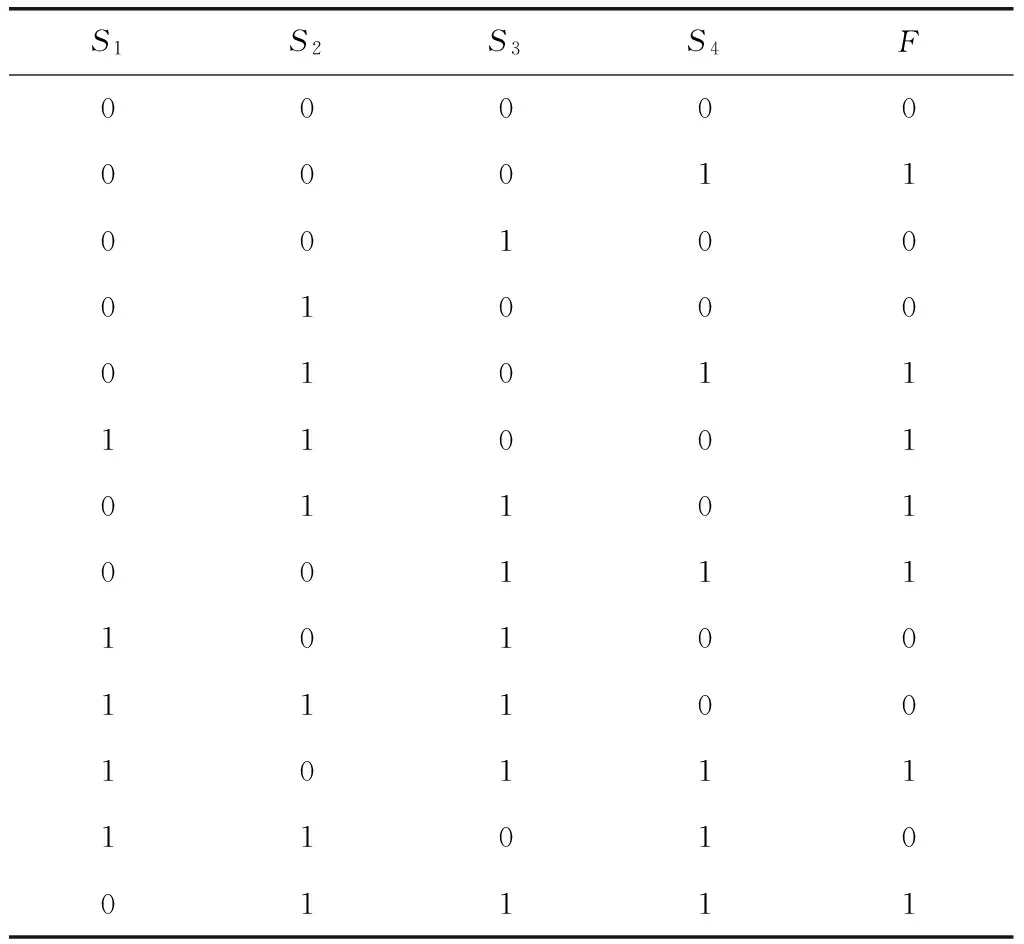
表1 输入数据集

S1-S4表示传感器；根据给定规则，将它所获取到的数据转化为二进制数据；F事件在二进制数据里出现情况(1：出现；0：未出现)，取决于S的值。

本文算法进行预处理后对表2数据进行挖掘得到的结果，如表2所示。

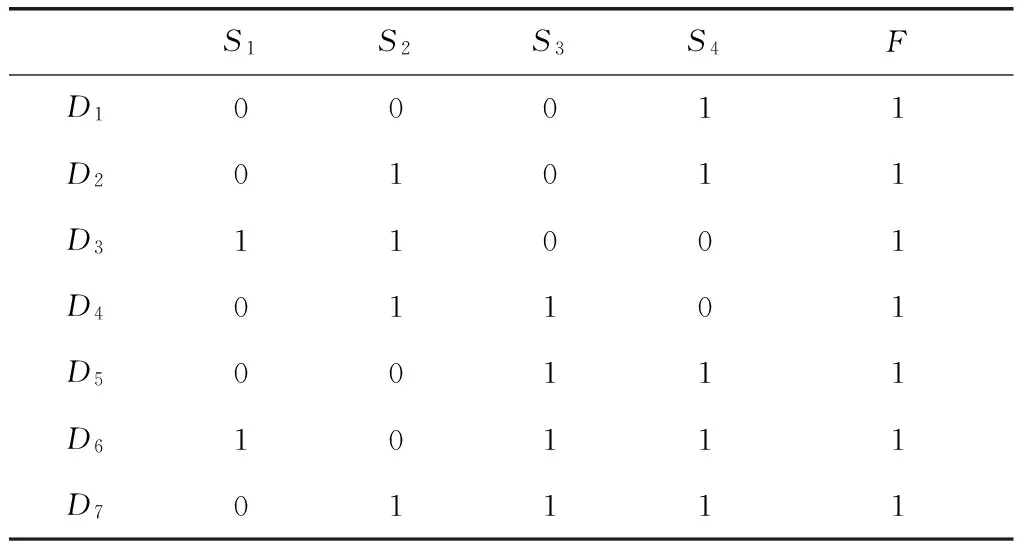
表2 预处理的数据值为1

利用表2里F值为1的行而形成的数据集；APRIORI概率PPij，PPij由表2的数据得到如表3所示。

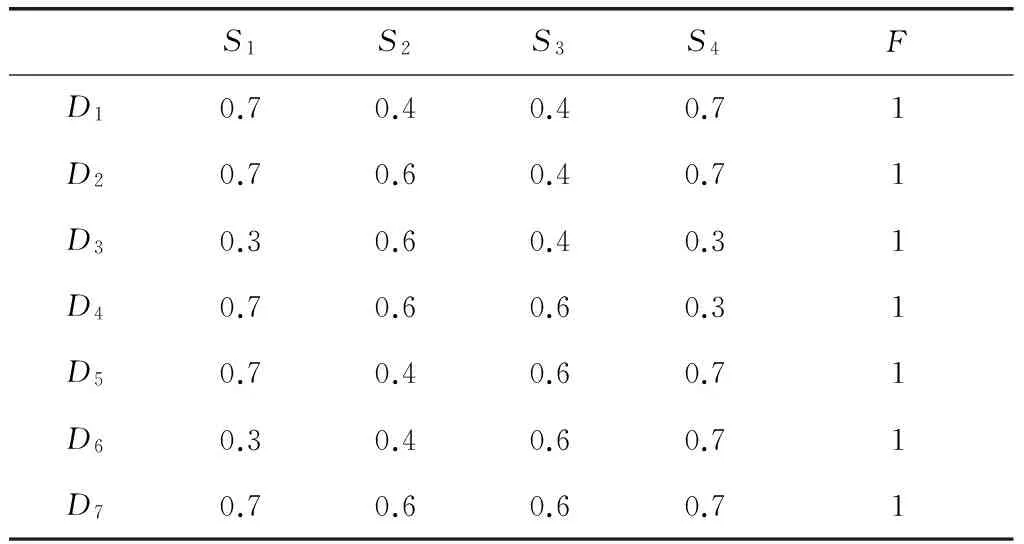
表3 表2数据的先验概率

PPij表示Sj的APRIORI概率Di。APRIORI概率是传感器值的百分比。例如，表2有7行，每一行都存在0值；所以S1的0值百分比计算为5/7=0.7；0.3是1值的百分比。同样，S2的0值是3/7=0.4。

根据贝叶斯理论，将后验权重分配给表3的数据。由式(5)可得到Di的后验权重Wi。

(5)

在式(5)，n表示传感器的数目；Wi是Di的平均后验概率。由式(5)得到的权重，如表4所示。

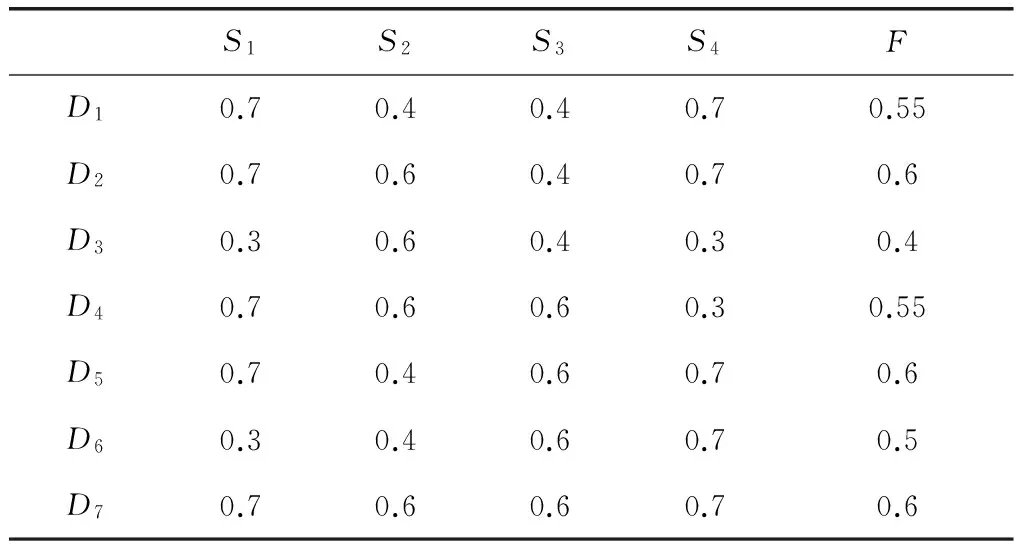
表4 表3数据的权重

因为其权重小于最小权重0.5，所以要删除D3，才能保证关联规则简化所需的置信度和支持度。

2.3 规则的简化

采用本文的WTabular算法对规则进行简化。在移除权重低于最小权重的规则后得到的规则，如表5所示。

表5 简化后的规则

当表5中，数据f=1时，应用后处理环节步骤4的初次简化；初次简化后得到的结果，如表6所示。

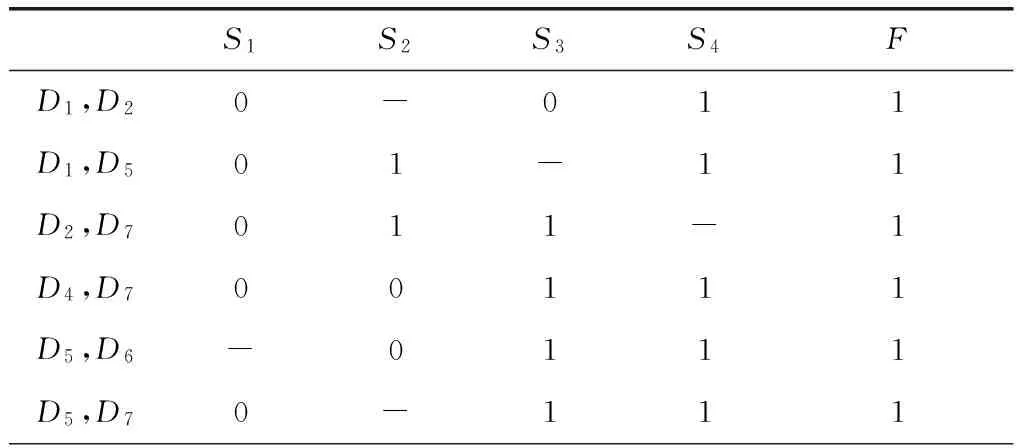
表6 初次简化的结果

在初次简化之后，反复采用后处理环节的步骤5和步骤6直至不能简化。表7给出二次简化后的结果，如表7所示。

表7 二次简化后的结果

最后得到的关联规则，如表8所示。

表8 最后关联规则

2.4 关联规则的评价

根据式(1)和式(2)定义的方程，假设存在规则，表7的{S4}→f，其支持度和置信度均为100%。利用APRIORI算法，可计算{S4}→f满足表1最小支持度20%的支持度和置信度，分别是38%和87%。APRIORI算法和WTabular算法的简化率分别大约是69%和92%。由上述例子可知，本文提出的WTabular算法无论在支持度和置信度还是规则的简化率方面都要优于APRIORI算法。

3 实验结果与讨论

本文采取计算机模拟实验来评估本文算法的性能。实验采用的系统是INTER2.8Ghz酷睿2四核CPU，8GB RAM，32位Windows7；模拟代码是Visual studio 2010的C++语言。

同时对APRIORI算法和FP增长算法进行评估；将它们与文中WTabular算法在数据规模不断变化情况下对置信度、支持度、规则简化率和数据处理速度的表现进行比较。

实验数据库取自人体感知的数据，随机创建而成，具有7个预处理和两个后处理属性。每个数据项以二进制来表示，如果比阈值大,值就是1；否则为0。例如，如果权重正常，是0；否则是1。实验用到的数据集大小从10万逐渐扩大到100万。

选择规则{S5}→f1时，数据规模不同情况下三种算法的支持度和置信度比较结果，如图2、图3所示。

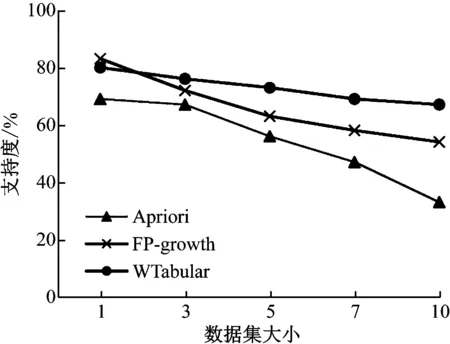
图2 三种算法的支持度比较结果

图3 三种算法的置信度比较结果

由图2可知文中算法的支持度和置信度均优于另两种算法；而且，本文算法的规则简化率最高，如图4所示。

图4 规则简化率比较

所以，本文算法适合于通过快速对比最小数据，并且又保持较高置信度来提供准确服务社会化计算领域。

不同数据规模情况下规则挖掘次数的对比结果，如图5所示。

当数据相对较小在50万以下时，文中算法用时比FP增长算法稍长；但对更大规模的数据运算更快。所以我们认为

文中算法更适合用来处理大数据。

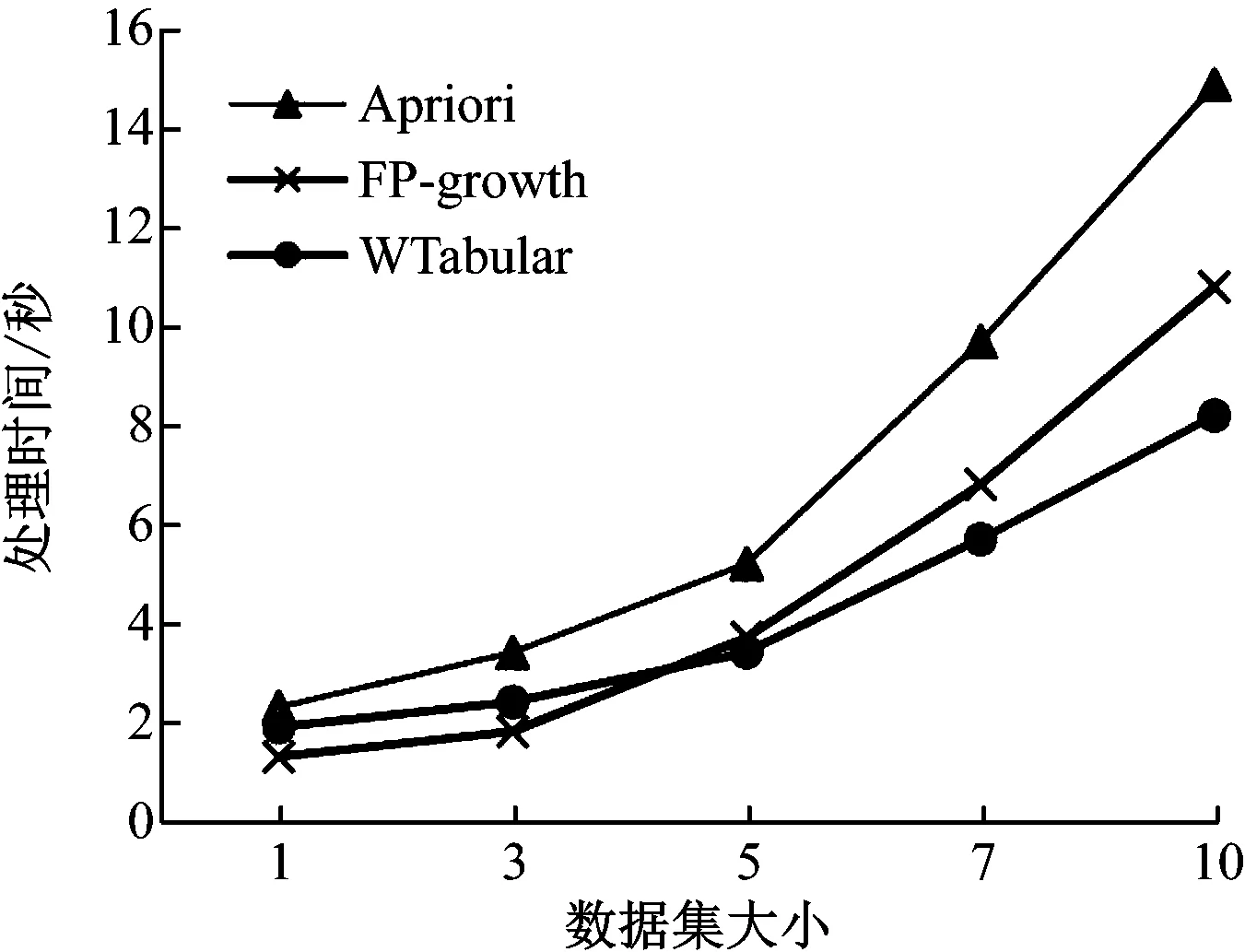
图5 数据处理时间比较

4 总结

对给定数据集的关联规则进行简化是处理大规模数据的社会化计算领域一个非常重要的问题。目前，已有许多研究提出利用属性分类学和负关联规则的做法来有效简化数据并找出关联规则。本文提出WTabular算法是通过去除不满足最小权重的数据并利用奎因-麦克拉斯基简化方法来达到对关联规则的数目进行删减的目的。通过计算机模拟实验，发现本文算法的支持度、置信度、规则简化率和数据处理时间都较现有方法有所改善。

今后研究的重心在于该算法对流动数据的实时处理方面。关注传感器实时收集无格式的流数据。因此，有必要对关联规则简化方面的方法论进行研究，以便不需要将无格式数据转化为二进制数据而直接进行处理。而且，还要考虑通过语义传感器网提前建立传感器之间的关联来提高关联规则简化的效果；并在多种领域和不同规模数据集方面对其进行验证。

[1] 程学旗,靳小龙,王元卓,等. 大数据系统和分析技术综述[J]. 软件学报,2014,09:1889-1908.

[2] 张峰. 基于网络化数据分析的社会计算关键问题研究[D].北京：北京邮电大学,2014.

[3] 陈翔,徐佳,吴敏,等. 基于社会行为分析的群智感知数据收集研究[J].计算机应用研究,2015,12:3534-3541.

[4] 陈爱东,刘国华,费凡,等. 满足均匀分布的不确定数据关联规则挖掘算法[J]. 计算机研究与发展,2013,S1:186-195.

[5] 张玺. 数据挖掘中关联规则算法的研究与改进[D].北京邮电大学,2015.

[6] Chiu H P, Tang Y T, Hsieh K L. Applying clusterbased fuzzy association rules mining framework into EC environment[J]. Applied Soft Computing, 2012,12(8): 2114-2122.

[7] Sun D, Teng S, Wei Zhang, Haibin Zhu. An Algorithm to Improve the Effectiveness of Apriori[C]∥International Conference on Cognitive Informatics, 2007:385-390.

[8] Zhang W, Liao H, Zhao N. Research on the FP Growth Algorithm about Association Rule Mining[J].International Seminar Business and Information Management, 2008:315-318.

[9] Nelson V P, Nagle H T. Digital Logic Circuit Analysis and Design[M]. Prentice Hall, 1995.