关于水产科学研究中II型错误的引申思考

王迎宾，孙 洁

(浙江海洋大学水产学院,浙江舟山 316022)

统计学中的I型错误和II型错误(即弃真和纳伪),是显著性检验内容中的两个基本概念。在假设检验中,这两类错误难免会出现,主要是由假设检验所使用的理论基础—“小概率事件不可能性原理”导致的。这一问题在很多的统计学或生物统计学教材中均有详细的阐述[1-2]。两类错误中,II型错误受到的重视程度不及I型错误,其直到上世纪30年代才逐渐得到学者们的关注[3]。较早是在医药学研究中被提及[4-5],主要应用在药效分析当中。在水产学研究中,国外最早是在上世纪80年代才对II型错误给予关注,而我国在这方面的研究几乎是空白,仅王迎宾等[6]在2016年发表文章,对此问题进行了专门讨论。在这篇文章中,作者举例阐述了II型错误产生的原因、影响因素和检验效能(1-β)的计算方法。该方法是教科书中提供的经典方法[1,2,7],使用该方法计算出来的检验效能被称为观测效能(observed power)[8]。

在王迎宾等[6]的文章中指出,不管是显著性水平α、样本容量、标准差σ等因子,都是与显著性检验的P值相关的,即P值的大小会影响到检验效能的大小。这一点在BROSI,et al[7]以及HOENIG,et al[8]的研究中均有提及。经典方法计算得到的检验效能与P值大小的关系,主要表现为随着P值的增大检验效能逐渐降低。当P值大于显著性水平α时,表明接受检验的两者差异不显著,此时拒绝原假设,接受备择假设,从而有犯II型错误的可能。但与此同时,使用经典方法计算得到的观测效能也通常小于50%[7-8]。也就是说,当检验得到的P＞α时,可能犯II型错误,但此时如果使用经典方法计算β的话,其结果会一直大于50%,即检验效能不会超过50%。相反,当P＜α时,接受检验的两者差异显著,此时可能犯I型错误,而非II型错误。虽然此情况下能够计算得到较高的观测效能值,但意义已经不明显了。而当P=α时,β=50%。因此,有学者提出,在计算检验效能时,应尽量避免使用经典方法[7-8]。

在α值较大或者样本容量较大时,经典方法尚能够发挥其作用[6]。但当检验水平较高,即α值较小,或者为小样本时,经典方法所能提供的信息就十分有限了。水产科学研究充满了不确定性,对检验结果的要求与某些学科相比要低(如医学等)。但α值一般也要设定在5%左右,最多放宽到10%。此外,水产科学所用的科研样本相对其资源总体而言,只能视为小样本。这样,在水产科学研究中,使用经典方法计算检验效能时,通常不会得到较大的值[6]。因此,若有更为完善的计算方法,将能够提高检验效能计算的可靠性。

1 等效性检验

传统的差异性检验方法往往无法对实际差异的大小进行评价,也不能说明差异是否具有实际意义。因为,很多检验假设并不是一个点,而是一个区间,这一点在医疗、医药行业尤其明显。此时需要使用等效性检验(equivalence testing)来判断两者的等效性。此外,等效性检验在计算检验效能方面也比经典方法具有优势。

安胜利[9]在讨论传统的差异性检验与等效性检验的关系时,曾提出等效性检验的检验效能计算公式。BROSI,et al[7]以及HOENIG,et al[8]也提出使用等效性检验的方法,即通过颠倒传统差异性检验中的无效假设和备择假设的方式,来计算检验效能的大小。

在等效性检验中,同样有I型和II型两类错误,这与传统差异性检验相同。但原假设H0与备择假设H1的定义与传统检验有所不同。在等效性检验中,I型错误也用α表示,指当事实上两者为不等效时,却误认为等效(拒绝H0,接受H1);II型错误同样用β表示,指当事实上两者为等效时,却没能下等效性结论(接受H0)。使用等效性检验就将传统差异性检验中的纳伪错误控制在了α水平内,而此时传统上的弃真错误则为β,检验效能计算的是当事实上两者等效时判断正确的概率。

2 检验效能的计算

等效性检验首先需要设定1个无效假设,即假定两者不等效,然后检验无效假设是否成立[8,10-11]。该方法的主要难点之一是研究者必须事先针对要检验的两者设定一个最小差异,称为等效界值(effect size,△),依据该值对两者之间是否存在显著差异进行判断。研究者事先设定的△要求十分明确,不能含糊。

下面以两独立样本平均数差异性检验为例,来展示等效性检验计算检验效能的方法。根据JONES,et al[12]的描述,开展等效性检验需要以下几个步骤：

(1)基于对研究对象特征的了解,设定等效区间[-△,+△],(区间并不一定对称)[10]。

(2)计算置信区间：置信限=估计值±关键值×标准误,即

(3)绘出置信区间和等效区间(具体可参考JONES,et al[12]文章中的图5),通过判断两者之间的包含关系,来评估差异的显著性情况。

安胜利[9]提出了基于等效性检验的检验效能计算公式。以两样本均数等效性检验为例,其检验效能计算公式为：

式中n为每组的样本量(假定两组样本量相等),Φ(x)表示标准正态分布下x左侧的面积。

下面采用王迎宾等[6]文章中的例子,使用等效性检验方法对两样本等效性进行判断,计算检验效能大小。假设几年前某资源群体渔获物平均体长为220 mm,如今想要检验经过几年捕捞后,该资源群体是否处于过度捕捞状态？使用t检验,在α=0.05水平下,检验该资源群体渔获物平均体长是否显著小于220 mm？采集该资源群体渔获样本50尾,测量得到样本平均体长为218 mm(标准差σ=20)。

根据差异性检验方法,显著性检验结果表明捕捞前后两者平均体长差异不显著,即没有发生过度捕捞。此时,经典方法计算得到犯II型错误的概率为82.36%,检验效能等于17.64%[6]。

使用等效性检验判断显著性水平情况,首先根据该种类的捕捞情况和生物学特征,等效界值△设定为5 mm,这样等效区间就等于[-5,+5]。置信区间根据公式(1)求算,得到置信下限CL-=-3.684,置信上限CL+=7.684。可以看出,置信区间左侧部分包含在等效区间之内。据JONES,et al[12]提供的判断标准,此时两样本平均数既差异不显著,也不等效,这与t检验结果一致。使用公式(2)计算检验效能,结果为

3 影响检验效能的因素

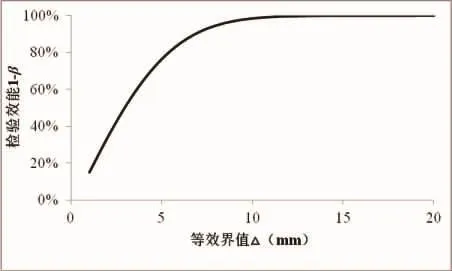
图1 不同等效界值条件下等效性检验的检验效能值（显著性水平α=0.05，样本数量n=50，标准差 σ=20）Fig.1 Statistical power calculated using equivalence testing under different effect sizes(significant level α=0.05,sample size n=50,standard deviation σ=20)

根据公式(2)可知,检验效能值会受到等效界值△、样本数量n、标准差σ和显著性水平α大小的影响。

3.1 等效界值（区间）大小对检验效能的影响

研究者事先所设定的等效界值(区间)的大小,对检验效能的影响十分明显(图1)。从图1可见,当△在8 mm以内时,检验效能随着△增加而迅速增大;当△大于8 mm以后,检验效能增加幅度就非常小了。当△较小时,表明研究者所能允许的捕捞前后鱼类体长的变化较小,即在捕捞影响下,即使鱼类体长稍有减小,也将认为体长变化显著。此时,原假设更容易被接受,从而II型错误概率较大。相反,当△设定的较大时,表明研究者能够接受较大的体长变化,即使捕捞前后体长减小较多,也认为体长没有显著变化。此时,原假设不易被接受,两者更容易被认为等效,从而I型错误概率较大。

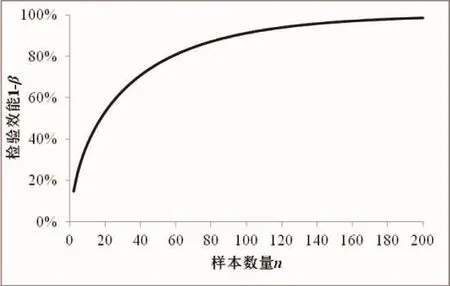
图2 不同样本数量条件下等效性检验的检验效能值（显著性水平α=0.05，等效界值△=5，标准差σ=20）Fig.2 Statistical power calculated using equivalence testing under different sample size(significant level α=0.05,effect size △=5,standard deviation σ=20)

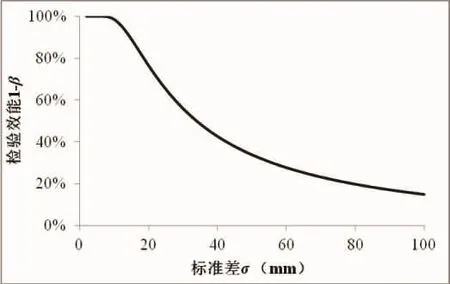
图3 不同标准差条件下等效性检验的检验效能值（显著性水平α=0.05，等效界值△=5，样本数量n=50）Fig.3 Statistical power calculated using equivalence testing under different standard deviation(significant level α=0.05,effect size △=5,sample size n=50)

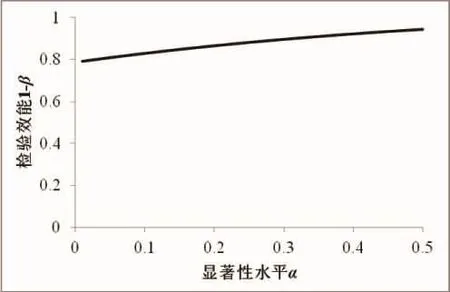
图4 不同显著性水平条件下等效性检验的检验效能值（等效界值△=5，样本数量n=50，标准差σ=20）Fig.4 Statistical power calculated using equivalence testing under different significant level(effect size△=5,sample size n=50,standard deviation σ=20)

3.2 样本数量对检验效能的影响

图2 显示,随着样本数量增加,检验效能增大,特别是在样本数量小于50时,检验效能增加十分明显,样本数量大于50以后增长速度就放缓了。根据求算置信区间的公式(1)可以看出,样本数量增加会使置信区间变小。根据BROSI,et al[7]的理论,在△不变情况下,置信区间减小,相对而言可视为等效区间变大。根据3.1节的分析,△增加会使检验效能随之增大。

3.3 标准差对检验效能的影响

标准差σ对检验效能的影响同样明显(图3),随着σ的增大,检验效能显著下降,并且下降速度逐渐变缓。标准差大,意味着数据更加分散,从而置信区间也就更大。这样就和3.2节所讨论的情况相反,置信区间大,等效区间2△就相对变小,因此,检验效能便出现随着σ的增大而降低的趋势。

3.4 显著性水平对检验效能的影响

显著性水平α与犯II型错误的概率β两者是呈负相关关系的,即在其他条件不变情况下,α增大同时β就会减小,因此1-β就会增加(图4)。这也与王迎宾等[6]的研究结果一致。从图4可以看出,与其他影响因素相比,显著性水平对检验效能的影响并不显著。当等效界值、标准差、样本数量等确定以后,随着显著性水平变化,检验效能增加十分平缓。由此可见,要增加检验效能,合理的等效界值以及样本的性质是更为重要的因子。

4 讨论

检验效能用来表示避免II型错误的大小,II型错误往往不如I型错误受重视,因此其危害也可能会被低估。这一点在水产科学研究中十分明显,除了上文介绍的例子以外,还有很多。例如,捕捞学选择性研究中,为了达到保护渔业资源,释放小个体鱼类的目的,需要放大渔具的网目尺寸。为了检验放大网目尺寸后,所捕获鱼类个体尺寸是否有显著增加,需对放大网目尺寸前后渔获样本的平均体长进行显著性检验。(2捕捞前后渔获样本平均体长差异不明显),HA：μ1≠μ2。如果检验结果导致II型错误,则会错误地接受原假设,即事实上放大网目尺寸后,捕获个体显著增大,但却未能接受该结论,而是认为前后尺寸差异不显著。此时,渔业管理者可能会采取两种措施：一是管理人员觉得放大网目尺寸意义不大,从而保持网目尺寸不变,这样资源遭受的捕捞强度没有降低,资源将进一步衰退;另一种是继续放大网目尺寸,直到检验结果差异显著为止,此时渔获物尺寸虽然显著增大,但是产量势必会大幅降低,导致渔民不必要的减产减收。水产养殖工作中也有同样问题,例如为了降低养殖种类患病比例,需要使用新的药物,新药物使用后检验患病率是否比以前有显著下降。同样,H0：p1=p2(使用新药后患病比率没有显著下降),HA：p1≠p2。此时,若犯II型错误,表明事实上使用新药后患病个体明显减少,但却认为新药效不明显。此时,管理者或养殖者同样有两种选择：一是不使用新药,结果是患病率无法得到有效降低;二是选用药效更好的新药,直到检验结果药效显著,但此时新药的成本也必然会大幅提高,造成不必要的收益降低,甚至亏损。在水产科学研究中,类似的例子还有很多,这些例子的特征之一就是II型错误导致了严重的后果,甚至比I型错误更加严重。因此,在水产学研究中,II型错误必须得到重视,同时还要进一步探索更多计算检验效能的方法,来提高检验结果的准确性。

本研究结果显示,检验效能的变化受到α、样本数量等因素的影响特征与王迎宾等[6]的研究结果基本一致,即随着α和样本容量的增加,检验效能均呈现出增大趋势。但是,差异检验的结果受到α的影响更加显著,当α从0.01增加到0.05时,差异检验得到的检验效能变化幅度达到12.06%[6],而等效性检验的变化却只有1%左右。此外,当样本较小时,随着样本数量增加,等效性检验的结果影响更加明显,当样本数量继续增加,其影响对差异性检验的结果则更为明显[6]。已经有学者指出,基于差异性检验的经典方法计算检验效能存在局限性,即检验效能与P值呈负相关[7-8]。当P值大于显著性水平α时,检验效能不会超过50%,这样经典方法能提供的有效信息就十分有限,特别是在α值较小,或者为小样本的时候尤其明显。王迎宾等[6]的文章重点讨论了不同因素对差异性检验的经典方法计算检验效能的影响情况,对上述检验效能与P值存在相关性的问题并未做深入探讨。本文则重点讨论了该问题,并建议使用等效性检验方法来计算检验效能,以得到更为科学的结果[7-8]。

等效性检验与差异性检验是两类不同的检验方法。人们对差异性检验中的原假设和备择假设是很熟悉的,通常原假设为“两者差异不显著”,备择假设与其相反,“两者差异显著”。但是,有人不禁要问：为何原假设不能是“两者差异显著”呢？此时,得到的回答往往是诸如“简单原则”或者“对于科研工作而言,犯弃真错误更加严重”等等,这样的回答是不充分的[8]。正如上文所列举的例子一样,在水产学研究中,纳伪错误可能导致更为严重的后果[6]。在实际应用当中,原假设和备择假设颠倒选择并非不可以。等效性检验关于原假设和备择假设的描述,与其在差异性检验中就有所不同,原假设为两者不等效,而备择假设则为两者等效。此外,差异性检验的目的是推断两个总体是否达到了统计学上的显著水平,其检验假设是针对一个点;而等效性检验的目的是推断两个总体的差异是否在某个范围之内,其检验假设是针对一个区间[13]。因此,等效性检验通常结合置信区间和研究者设定的最小差异,即等效界值,对检验结果进行判断[10,14-15],并且检验效能的计算同样依赖于界值的大小。

差异性检验和等效性检验两种方法计算的检验效能所表达的含义是不同的,这主要是由两种检验方法的假设条件不同造成的。差异性检验中,II型错误指当事实上两者差异显著,却不能下两者差异显著结论的概率,这样检验效能即为事实上两者差异显著,并能下两者差异显著结论的概率。而在等效性检验中,II型错误指当事实上为两者等效时,却不能下等效性结论的概率,此时检验效能指当事实上为等效时,能够获得该结论的概率[9]。在等效性检验中的I型错误,即事实上为两者不等效时,却未能下不等效性结论的概率不会超过α。由于α值是由研究者事先设定好的,因此,等效性检验中的I型错误(类似差异性检验中的II型错误)的概率就是直观受控的了。同时,等效性检验中的II型错误(类似差异性检验中的I型错误)的概率可以使用公式(2)直接计算。差异性检验和等效性检验的假设、计算和两类错误的表述均有差异,使用时需要格外注意。

等效界值的确定,并非随意和盲目的,必须有一定的意义。对于水产科学而言,界值的确定就须有实际的生物学意义。比如,要判断捕捞作用下,某种鱼类平均体长是否减小了,此时等效性检验就需要设定一个能够反应平均体长发生变化的最小界值,而这个界值的确定须是通过实验研究,或者由专家基于经验提出,以保证其生物学意义。尽管有以上要求,但是在界值确定过程中也难免会有主观成分[16],这也就提醒研究者应尽可能多渠道地搜集相关信息,来提高界值的准确性和科学性。同时,我们也应意识到,等效界值与检验效能是有相关性的(图1),并不是等效界值越小就越好,其值越小检验效能就越小,这样反而增加了II型错误的可能性。等效界值的确定应本着客观、科学的原则,既不能追求越小越好,也不能随意放大。

除了等效界值以外,还有其他因子同样会影响检验效能,比如样本数量、标准差、显著性水平等等(图2-图4)。样本数量越大越有利于降低II型错误,但与此同时成本也会增加。标准差反映着样本的性质,也与样本大小有关。而显著性水平是研究者根据研究需求而事先定好的。这些因子都将对检验效能产生影响,因此,对其选择也应视具体情况而定,基于现有条件和研究要求,选择合适的因子水平,得到理想的计算结果。

虽然在一些统计学教材中介绍了检验效能的计算方法,但计算过程并不简单,特别是对于统计学基础薄弱者而言,很难将这些方法直接应用到实际的研究和工作中。因此,在今后在的研究中,我们将开展检验效能计算程序(VBA和R语言)的开发的工作,使检验效能计算模块化,方便科研工作者和管理者使用。

[1]杜荣骞.生物统计学[M].第3版.北京：高等教育出版社,2009：80-85.

[2]GLOVER T,MITCHELL K.生物统计学导论[M].北京：清华大学出版社,2001：120-125.

[3]TANG P C.The power function of the analysis of variance tests with tables and illustrations of their use[J].Statistical Research Memoirs,1938,2：126-149.

[4]ANDRSON S,HANCK W W.A new procedure for testing equivalence in comparative bioavailability and other clinical trials[J].Communication in Statistics-Theory and Methods,1983,12(23)：2 663-2 692.

[5]SCHUIRMANN D J.A Scomparison of the two one-sided tests procedure and the power approach for assessing the equivalence of average bioavailability[J].Journal of Pharmacokinetics and Biopharmaceutics,1987,15(6)：657-680.

[6]王迎宾,俞存根,陈 勇.水产科学研究中被忽视的II型错误[J].水产学报,2016,40(1)：135-143.

[7]BROSI B J,BIBER E G.Statistical inference,Type II error,and decision making under the US Endangered Species Act[J].Frontiers in Ecology and the Environment,2009,7(9)：487-494.

[8]HOENIG J M,HEISEY D M.The abuse of power：The pervasive fallacy of power calculations for data analysis[J].The American Statistician,2001,55(1)：19-24.

[9]安胜利.传统假设检验与等效性检验关系的模拟研究[D].广州：第一军医大学,2007：3-9.

[10]WELLEK S.Testing statistical hypotheses of equivalence[M].Boca Raton,FL：CRC Press,2002：1-431.

[11]MCGARVEY D J.Merging precaution with sound science under the Endangered Species Act[J].BioScience,2007,57(1)：65-70.

[12]JONES B,JARVIS P,LEWIS J A,et al.Trials to assess equivalence：the importance of rigorous methods[J].British Medical Journal,1996,313：36-45.

[13]安胜利,陈平雁.等效性检验与差异性检验的区别及其模拟验证[J].中国卫生统计,2007,24(3)：226-228.

[14]SOKAL R R,ROHLF F J.Biometry：the principles and practice of statistics in biological research[M].3rd edn.New York,WH Freeman and Company,1995.

[15]ADELMAN D E.Scientific activism and restraint：the interplay of statistics,judgment,and procedure in environmental law[J].Notre Dame Law Review,2004,79：497-583.

[16]WAPLES R S,GAGGIOTTI O.What is a population An empirical evaluation of some genetic methods for identifying the number of gene pools and their degree of connectivity[J].Molecular Ecology,2006,15(6)：1 419-1 439.