基于改进蚁群算法的水产品运输车路径优化策略

李鹏飞，沈最意

(1.浙江海洋大学港航与交通运输工程学院,浙江舟山 316022;2.浙江海洋大学经济与管理学院,浙江舟山 316022)

我国东部海洋资源分布广,东南方沿海城市是我国水产品企业聚集区域。目前,国内市场上鲜活水产品的需求量增长迅速,加之水产养殖业的发展进程加快,与水产品息息相关的冷链物流建设逐渐表现出高速发展的趋势。但中国幅员辽阔,在水产养殖业较不发达的内地地区,人们对于鲜活水产品的需求更加难以得到实现,加之我国目前冷链布局分散,易腐产品在流通过程中得不到有效的质量保障,导致了水产品不同地域价格的巨大差异[1]。

而水产品的运输质量由冷链物流中3T原则(time、temperature、tolerance)的实现程度所决定。其中第一项就是指运输实时性,由于水产品冷链配送环节衔接的不紧密,容易出现断链现象,会对水产品质量产生不利的影响,则需要在配送过程中给各个需求点加上运达时间窗,而元启发式算法中的蚁群算法对解决具有时间窗的大型多回路路径规划问题(VRP问题)具有良好的天然适应性,虽然蚁群算法本身也存在着搜索时间长,过早收敛等问题。但通过公式的改进和参数的选取,这些不足都可以得到很好的改善。为此,国内外学者也提出各种改进方法。

1991年,在欧洲人工生命会议上,意大利学者COLORNI,et al[2]第一次提出了蚁群算法。随后为了国内外专家学者提出大量的改进方法,STTITZLE,et al[3]提出了MMAS算法,将信息素限制在一定范围内,防止出现信息素过度集中,提高了算法解的多样性。BULLNHEIMER,et al[4]发表了基于路径长度排序的蚁群算法,关键点是将每次迭代后,按照每只蚂蚁路径长度排列,只允许排名较前以及最优蚂蚁释放信息素;国内学者王颖等[5]提出了参数的自适应变化,提高了解的多样性,从而针对算法易得出局部最优解的弊端;闵克学等[6]利用蚁群算法易与其它算法相结合的优点,提出了一种将粒子群与蚁群优化相结合的算法,从而提高了全局迭代求解效果。

1 数学模型

1.1 水产品保鲜时间窗

每一种水产品都会有不同的耐藏性,假设某一种水产品的保质时间窗为(ready time,due time),service time表示完成服务所需要的时间,即service time(st)=due time(dt)-ready time(rt),主要依据客户接收货物的效率以及货物的量来设定。rt主要依据客户方便接受货物的时间决定,dt则是依据水产品的保质期限以及客户对该货物下一步的处理方式来确定,而st主要根据该客户点需求量的大小以及该点的服务。运输车辆须在时间窗[rt,dt]满足客户服务要求,如果运输车辆提前或者延期到达客户点,则必须承担一定的惩罚费用,并且客户有权拒绝所配送的水产品[7]。

1.2 不确定性路况描述

在水产品的运输配送中,可能会发生一些常发性交通拥堵例如上下班高峰期、假期等,从而导致配送效率的降低。此时,不应该认为各个客户点之间运输时间固定不变,而是具有相应的分布函数以及分布规律的随机变量。可将服从相应分布函数的不确定性路况条件转变为确定性条件,再加入到路径规划数学模型中求解。同时在大部分的实际状况下,配送过程中,准确的两点之间运输时间分布函数难以得知,但在不同时间内某一路段的运输时间长短(tij)的概率(pij)可以通过某些参考因素的定量分析和估算或者按照之前的运输经验得知。则可以通过经验分布得到该路段新的通过时间,即：

1.3 VRP问题运输模型描述

假设有一个水产品物流配送中心,各个需求点的坐标矩阵为C,其每辆水产品运输车的最大货物载重量为D,客户i的需求量为为di(i∈V),V客户集合,S为V的任一子集合。rti表示客户i允许卸载货物的最早时刻,dti表示客户i允许完成卸载的最迟时刻,sti表示完成卸货所需的时间,tij为运输车从客户i到客户j的运输时间,wi表示开始为i点供货所需的等待时间,a0是出车的单位成本,a1表示水产品不能在规定服务时间送达而增加的单位成本,ti表示货物到达点的时间,ei为客户i所容许卸货最早开始时刻,li为客户i容许卸货最晚开始的时刻[8]。基本假设条件为：(a)所有需求点和水产品物流配送中心的坐标位置已知;(b)各个需求点的供货量和水产品保鲜时间窗已知;(c)每个需求点只由一辆车经过一次;(d)运输车从水产品物流配送中心开始,通过几个需求点后返回配送中心,期间行驶方向是一直连续的,不能发生折返;(e)假定不确定性的道路通行状况服从相应统计分布,即某两点之间运输时间的概率分布在车辆运输之前是已知的。配送的目标函数为：

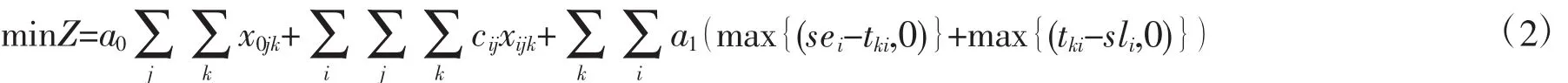
其中,包含四项：第一项为水产品运输车辆的出车成本。第二项为水产品运输车辆在路程上消耗的总运输费用。第三项为水产品运输车辆的时间惩罚成本,即运输车辆在时间窗之外到达所造成的违约金。其约束条件为：设

约束(5)为水产品运输车辆负载限制;约束(6)保证每个水产品运输车辆对每个客户只访问过一次;约束(7)～(9)保证了可行回路;约束(10)是某条道路上相邻任务并存的前提;约束(11)表示时间窗约束。

2 改进的蚁群算法

2.1 路径构造

设tik为第k辆车到达i点的时刻,为了在选择下一个客户点时,使等待时间较短的客户被选择作为下一运输点的可能性更大,在状态转移规则中加入等待因素

因此对状态转移概率公式进行如下修改：

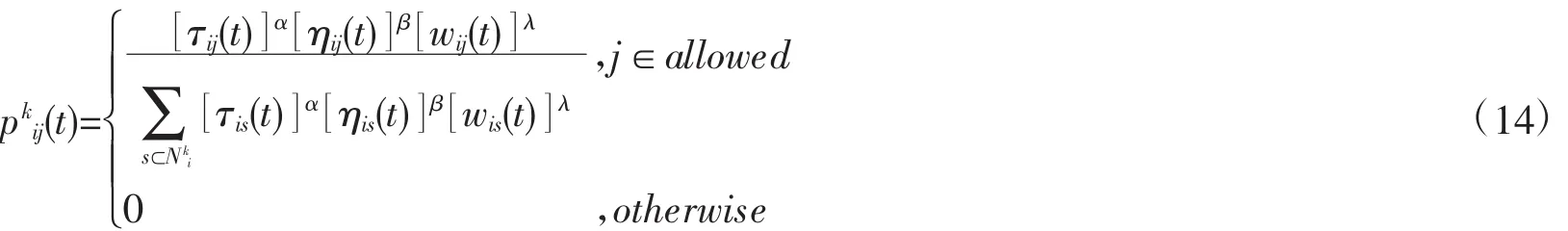
使用了伪随机比例规则,在解的快速收敛以及解的多样性之间取得较好的平衡。其中n0∈ [0.1]为一

2.2 信息素改进

2.2.1 信息素全局更新步骤

当m只蚂蚁都完成一次循环后,即所有蚂蚁构造完可行路径R时,将它与全局最优路径R*进行比较,其中

为了使每只蚂蚁的迭代运输方案对信息素增减产生正负反馈,依据图1规则使每一次迭代所有蚂蚁R上的信息素实行全局更新[9]：

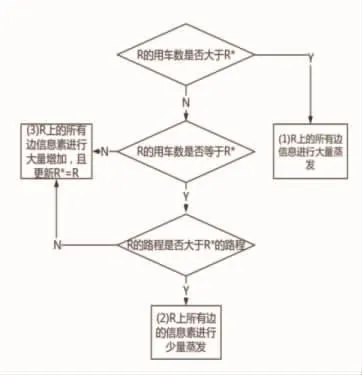
图1 全局信息素更新步骤Fig.1 Global pheromone updating steps

Q是一个常量,表示蚂蚁完成一次搜索所释放的信息素总量;L*为蚂蚁探索到的最优路径长度。ρ为信息素保留程度,在算法初期为了解的多样性可以取相对较大值,而在中后期为了最优解的快速收敛,使信息素较为集中,可以取较小值。

2.2.2 MMAS思想的引入

为了避免在初期陷入局部最优解,可以借鉴MMAS,对信息素在一定范围内进行限制,避免丧失摸索新路径的可能[11]。即

2.3 算法步骤

Step1：定义各参数,C,Q,α,β,λ,ρ,任意两点间路段上的信息素值初始为τmax,设定NC max为最大迭代次数。

Step2：将m只蚂蚁置于水产品配送中心点,并使该点置于当前解,采用依序构建解的方法。

Step3：对m只蚂蚁,根据式(13)计算转移概率,同时要求满足保鲜时间窗以及载重约束,选择除当前解集外的另一需求点,然后将其置于当前解中;若找不到满足运输车辆载重约束或时间约束的下一个节点时,则返回水产品配送中心[10]。

Step4：循环步骤(3),直至m只蚂蚁都到访了所有点,得到了相应条以水产品配送中心为起点并且满足约束条件的回路,每只蚂蚁的若干个回路相当于由配送中心所发出的若干个运输车辆所形成的配送路径,计算并保存最短路径R*。

Step5：根据2.2节所述方法实行全局更新以及对ρ进行调整,调整规则为：

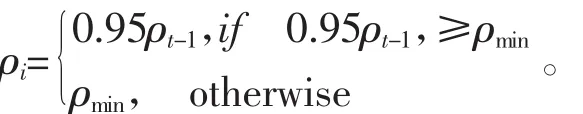
Step6：判断迭代数是否达到最大值,如果是,终止运输,不然则清空禁忌表,转到步骤2。

3 算例仿真

为了检验算法的性能,以舟山市地图为基础,通过MATLAB进行实例仿真实验。

在浙江省舟山市的百度地图上截取一部分平面交通图(图2),将水产品生产加工公司或者单位作为需求点,以舟山国际水产城物流配送中心为始发点。共有25个节点,其中1号节点为配送点(表1)。为了使得到的解更科学有效,进行了10次随机测试,10次测试中取得的最优试验结果并且与基本蚁群算法最优结果进行比较。

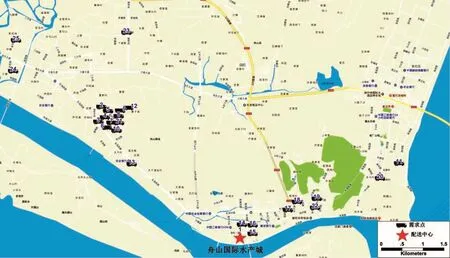
图2 平面交通图Fig.2 Flat road map

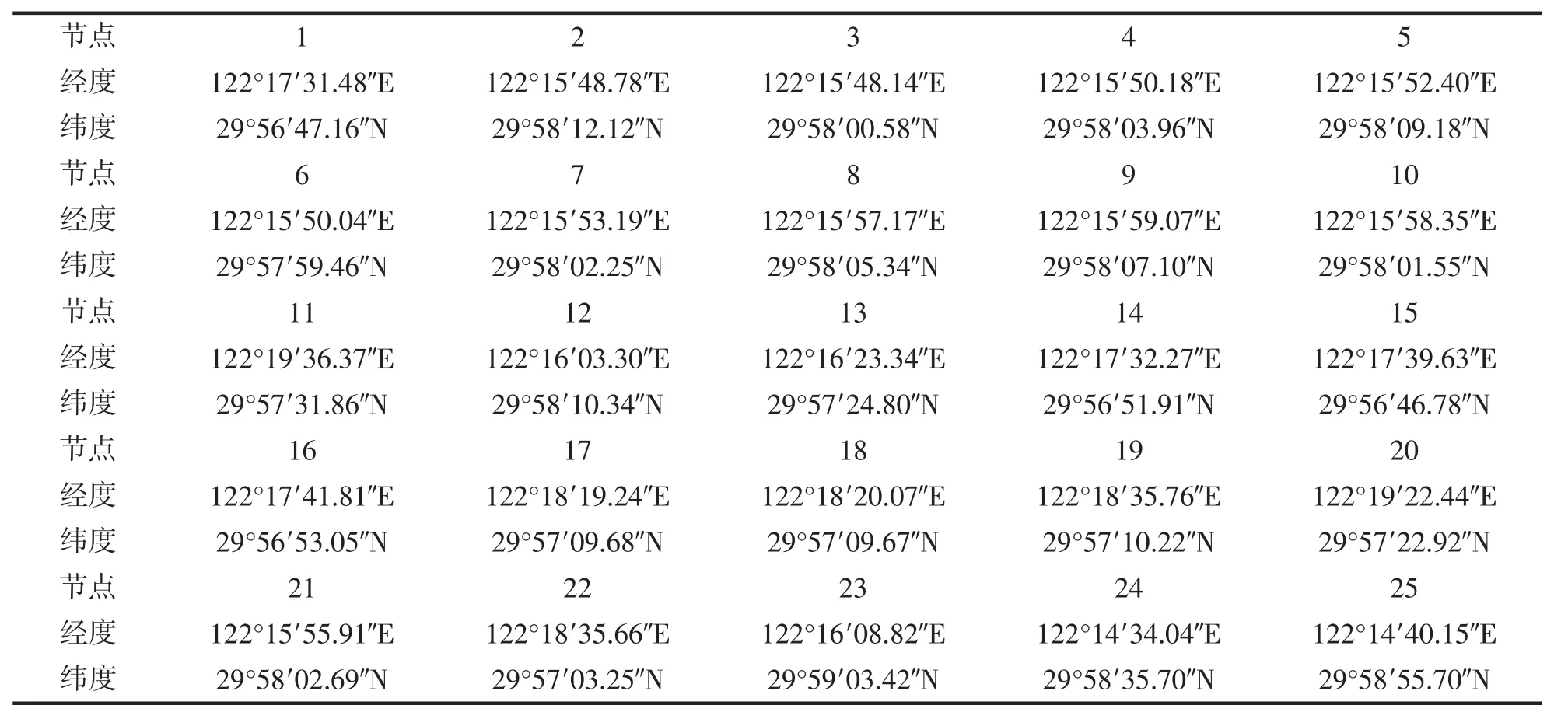
表1 节点经纬度Tab.1 Node latitude and longitude

m=30,Q=100,α=1,β=3,λ=1,ρ=0.9,τmax=1,τmin=0.3,迭代次数限制为 50 次,运输车速率为 40 km/h,水产品物流中心出车费用为100,单位公里车费为1,单位时间超前或延期惩罚费用为0.4,客户数量为24,目标函数曲线为运输总费用[12]。通过基本蚁群算法仿真的最优结果如图3～4所示。

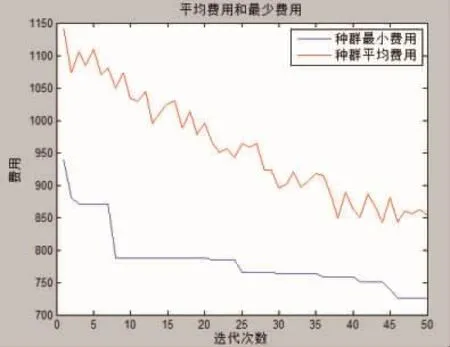
图3 基本蚁群算法迭代过程Fig.3 Iterative process of basic ant colony algorithm

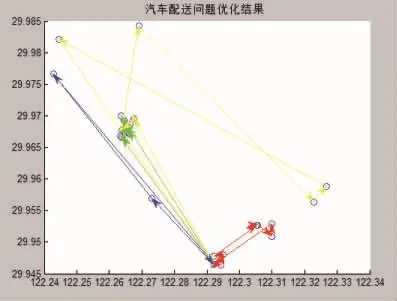
图4 基本蚁群算法最优路径Fig.4 The optimal path of basic ant colony algorithm

基本蚁群算法路径方案为：

(1)1-＞15-＞16-＞14-＞17-＞18-＞22-＞19-＞1

(2)1-＞6-＞3-＞8-＞10-＞21-＞7-＞5-＞2-＞1

(3)1-＞12-＞9-＞4-＞23-＞20-＞11-＞25-＞1

(4)1-＞13-＞24-＞1

Least_Cost=725.309 7

通过同样的参数,使用改进蚁群算法对舟山市部分地图上的水产品生产加工公司或者单位进行仿真实验,得出以下结果(图5、图6)。

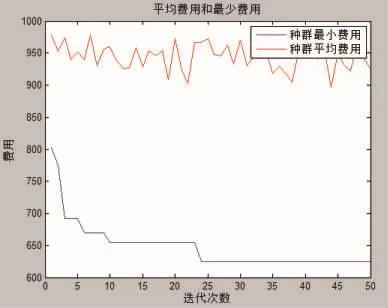
图5 改进蚁群算法迭代过程Fig.5 The iterative process of improved ant colony algorithm

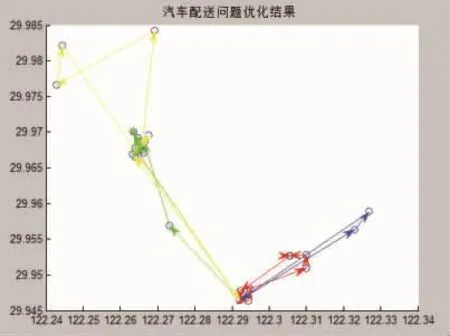
图6 改进蚁群算法最优规划路径Fig.6 The optimal planning path of the Improved ant colony algorithm

改进蚁群算法路径方案为：

(1)1-＞15-＞16-＞22-＞19-＞17-＞18-＞14-＞1

(2)1-＞13-＞9-＞7-＞21-＞10-＞2-＞5-＞4-＞1

(3)1-＞6-＞3-＞12-＞8-＞23-＞24-＞25-＞1

(4)1-＞20-＞11-＞1

Least_Cost=625.1464

从图3～6的对比可知,改进蚁群算法相对于基本蚁群算法得到全局最优解的迭代次数更少。求解效果方面,改进蚁群算法得到的最少总费用是625.146 4,基本蚁群算法得到最少总费用是725.309 7,并且种群平均费用两者也相差较大,可见路径规划方案的质量明显上升。表明改进的蚁群算法相对于一般的蚁群算法,可以通过相对较少的迭代得到全局最优解,并且收敛效果好,全局收敛效率高。

4 结论

运输配送是水产品冷链物流中至关重要的节点之一。选择合理、高效的运输路径有利于保证水产品的鲜活性,不仅节省了运输成本,并且加强了配送的准确性以及速率。针对水产品耐藏性较差的特点,提出了水产品的保质时间窗以及道路状况的不确定性,降低了可能由断链现象以及拥堵所造成的成本损耗,更加符合了配送作业实际情况。并且使用改进的蚁群算法求解该运输模型,包括信息素全局更新方法的改进、状态转移规则中等待因素引入以及信息素的限制等,最后利用MATLAB进行仿真模拟。仿真测试结果说明改进蚁群算法优于基本蚁群算法,是可靠有效的。

[1]李 利,江 敏,马 允,等.水产品保活运输方法综述[J].安徽农业科学,2009,37(15)：7 303-7 305.

[2]COLORNI A,DORIGO M,MANIEZZO V.Distributed Optimization by Ant Colonies[C].Ecal91-European Conference on Artificial Life,1992：134-142.

[3]STUTZLE T,HOOS H.MAX-MIN Ant System and local search for the traveling salesman problem[C].IEEE International Conference on Evolutionary Computation.IEEE,2002：309-314.

[4]BULLNHEIMER B,HARTL R F,STRAUSS C.A New Rank Based Version of the Ant System-A Computational Study[J].Central European Journal of Operations Research,1999,7(1)：25-38.

[5]王 颖,谢剑英.一种自适应蚁群算法及其仿真研究[J].系统仿真学报,2002,14(1)：31-33.

[6]闵克学,葛宏伟,张 毅,等.基于蚁群和粒子群优化的混合算法求解TSP问题[J].吉林大学学报：信息科学版,2006,24(4)：402-405.

[7]黄华芳,门建婷,陈绍慧,等.基于改进蚁群算法的果蔬运输车辆路径优化的研究[J].保鲜与加工,2011,11(3)：24-25.

[8]蒋 波.基于遗传算法的带时间窗车辆路径优化问题研究[D].北京：北京交通大学,2010：8-17.

[9]李 琳,刘士新,唐加福.改进的蚁群算法求解带时间窗的车辆路径问题[J].控制与决策,2010,25(9)：1 381-1 382.

[10]杨仁法,龚延成.带时间窗车辆调度问题的蚁群算法[J].交通运输工程学报,2009,9(4)：71-74.

[11]费瑞玉,马文华.基于邻域搜索的改进最大最小蚁群算法[J].计算机仿真,2014,34(12)：261-262.

[12]樊世清,娄 丹,孙 莹.生鲜农产品冷链物流车辆配送路径优化研究[J].保鲜与加工,2017,17(6)：106-111.