射流参数对风力机叶片气动性能的影响
王 龙,李 亮,孙伦业,王传礼
(安徽理工大学,安徽淮南 232001)
1 前言
风力机叶片作为风电设备的重要工作部件之一,其气动性能高低直接关系到发电功率输出。在来流大攻角条件下,风力机叶片会存在明显的流动分离现象,对水平轴风力机而言,其升力系数下降较为严重。因此大攻角来流条件下,风力机叶片的空气动力学问题应是研究重点之一[1,2]。
计算流体力学方法可用于模拟风力机运行过程中的流场结构,处理风力机叶片分离流动问题[3~5]。在叶片流动分离机理研究方面,国内外均进行相对深入的研究。Seifert 等对NACA0015翼型进行射流试验,研究表明在低马赫数条件下,射流可以提高升力系数,改善流动状况[6]。
Johansen等利用3D涡发生器对旋翼叶片进行计算分析,结果表明3D涡发生器有利于叶片流动分离控制,其控制效果与来流攻角密切相关[7]。高翔等采用CFD方法研究叶尖射流对叶片流场的影响,转速达到1200 r/min以上时,有利于风力机功率增加,尾缘后的叶尖涡耗散较快,可以有效改善风力机下游流场[8]。金琰等采用流固耦合方法研究风力机叶片颤振问题,在加入射流以后,叶片受激振动会得到明显抑制[9]。叶建等对低雷诺数下机翼翼型的前缘流动分离机进行研究[10],发现前缘椭圆弧靠近叶身位置存在吸力峰,并在强逆压梯度作用下发生流动分离;翼型上表面涡系结构包含驻留涡、脱落涡和二次涡,具有强烈的非定常性。
图1为分析射流参数对风力机翼型气动性能影响而采用的风力机叶片表面开缝示意,通过修改开缝位置及喷射角度,本文采用计算流体力学方法研究开缝位置及射流喷射角度改变对风力机叶片性能的影响。获取不同攻角下的叶片流场及升力系数,分析了流动分离机理,讨论了射流参数对流场及气动性能的影响。可为恶劣工况下风力机叶片设计研究提供参考依据。
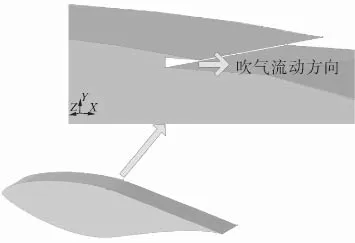
图1 风力机叶片表面开缝示意
2 控制方程及湍流模型
自然界所存在的流体满足质量守恒、动量守恒和能量守恒三大规律,在忽略源项的条件下,其数学积分的表现形式为:
ρ——密度矢量
v——速度矢量
π——应力张量
其牛顿流体的本构方程为:
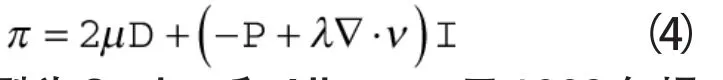
S-A模型为Spalart和Allmaras于1992年提出的一方程湍流模型[11],该方程在压声速和跨声速流动领域中的翼型及机翼应用广泛,但由于其只含一个湍流变量,因此相对于二方程模型来说计算量和耗时均较小。不引入转捩项的守恒型输运方程可改写为:
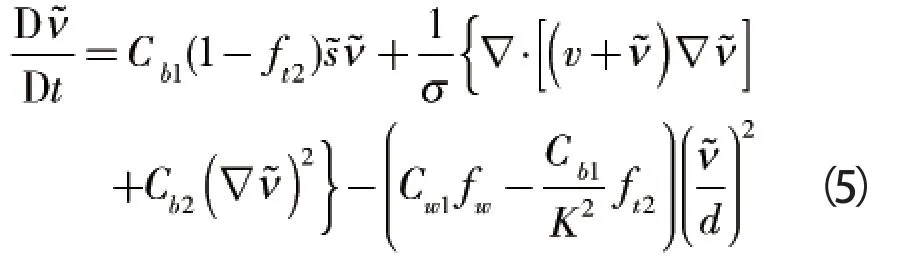
式中常数取值如下:Cb1=0.1355,σ=2/3,Cb2=0.622,其余表达式可参见文献[11]。
3 模型及网格
一般而言,大攻角下流动分离现象会出现在尾缘处,为提高射流效果,开缝位置位于x=0.5 m以后,喷射角度选择为2°,4°。同时根据开缝位置不同(分别为0.5,0.6,0.7,0.8 m处),依次命名为模型_1_A2、模型_1_A4、模型_2_A2、模型_2_A4、模型_3_A2、模型_3_A4、模型_4_A2、模型_4_A4,A2表示喷射角度为2°,A4表示喷射角度为4°。“模型_0”表示原型模型,即未开缝。
图2为风力机叶片模型及开缝模型示意,分别给出了本文计算所采用模型,为简单起见,仅给出了原始模型“模型_0”及开缝位置x=0.6 m的喷射角度为2°的模型_2_A2和喷射角度为4°的模型_2_A4对比。表1为射流开缝位置参数表,给出了开缝具体的坐标参数。
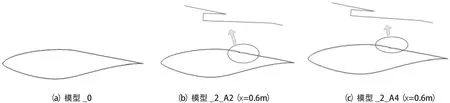
图2 风力机叶片模型及开缝模型
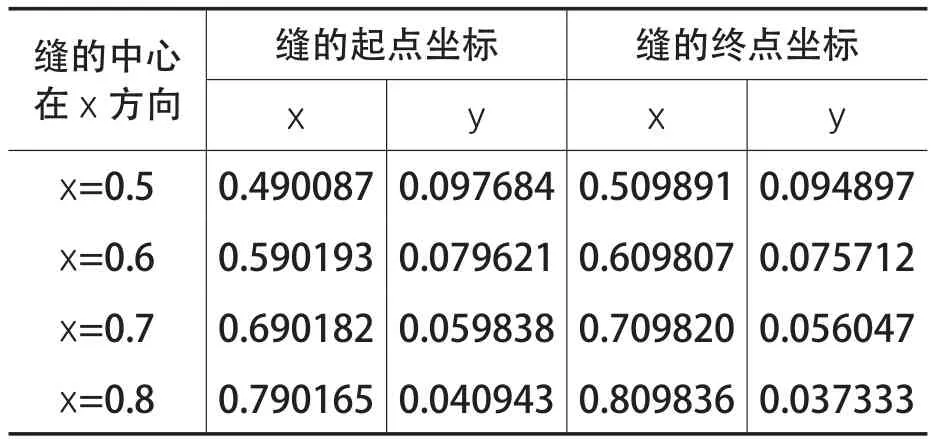
表1 射流开缝位置坐标 m
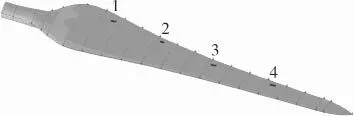
图3 三维叶片开缝位置
在三维叶片设计中,还需考虑开缝对叶片强度和刚度的影响。如对工程风力机三维叶片开缝,仅能采用离散型的方式,并且开缝的宽度不能过大,缝沿径向的尺度也应较小,才不会对叶片的强度和刚度产生影响,否则要考虑开缝对三维风力机叶片的强度和刚度影响。
图4为风力机翼型数值模拟所采用的计算域划分,计算域的上下边界为15C(C为弦长),为保证网格的正交性,计算域前部采用“C”结构,流体出口边界距离原点的距离为30C。边界条件由远场及壁面组成。
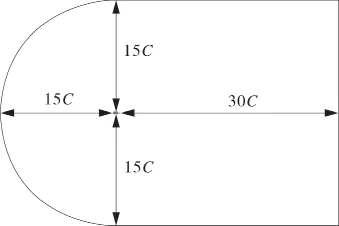
图4 计算区域
图5为风力机翼型数值模拟所生成的网格示意,包括整体网格及风力机叶片前后缘局部网格,近壁面第一层网格距离壁面约为1.0×10-5,总的网格数约为9万。
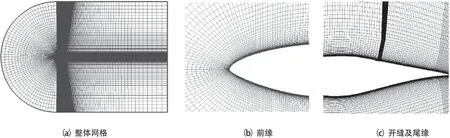
图5 网格示意
4 计算结果
所采用的计算条件如下:(1)计算攻角范围为12°~20°,计算间隔角度为2°;(2)对4个位置(即x=0.5 m、0.6 m、0.7 m、0.8 m)的开缝及原型模型计算,且缝宽均为2cm、喷射角度为2°和4°;(3)风速约为40 m/s,远场压力为72465 Pa,缝进口压力为74000 Pa。计算软件采用课题组自行开发的三维黏性NS方程求解器[12~14]。本文主要研究射流控制的效果,故选取极端天气下的风速40 m/s。远场压力为72465 Pa,缝进口压力为74000Pa,这里是为了研究射流效果而给定的一个计算参数,并不是风力机实际工作的压力参数。在此有意义的数据是远场压力与缝进口压力的差值,即差值Δp具有实际工程意义。
开缝的宽度选择有2个参考因素:(1)对三维风力机叶片而言,开缝只能沿径向位置以离散型分布存在,否则会对叶片带来强度等稳定性结构问题。因此开缝宽度不能过大。(2)Gilarranz等学者采用试验方法研究射流对航空飞机机翼的影响,节段翼型采用NACA0015,其开缝宽度为弦长的0.5%[15~19]。由于风力机所处的工作环境远没有航空飞机机翼恶劣,本文适当放宽缝的参数,选取缝的宽度为2 cm。考虑到本文所采用翼型弦长1 m,那么缝的宽度为弦长的2%,这种比值相对合理。
开缝角度理由如下,受S809翼型几何型面所限,在某些位置,喷射角度超过4°时已无法在叶片表面开缝,为比较相同参数下的射流效果,故研究的喷射角度选为2°和4°。
图6(a)、(b)分别为8种不同模型及原始模型叶片在攻角为12°~20°条件下的升力系数计算结果及均值比较。从图6可以看出,开缝后叶片在绝大多数计算状态下其升力系数均比原型叶片的升力系数有所增加,其最大无量纲均值增加的幅度在0.3左右。从图6还可以看出,x=0.5 m处位置的加入射流对升力系数提高最为有效,随着开缝位置坐标后移,其升力系数增幅不断降低,单一地改变喷射角度已不能满足改善流场的需求,射流位置参数在改善流场中所起效果显著,占据重要地位。
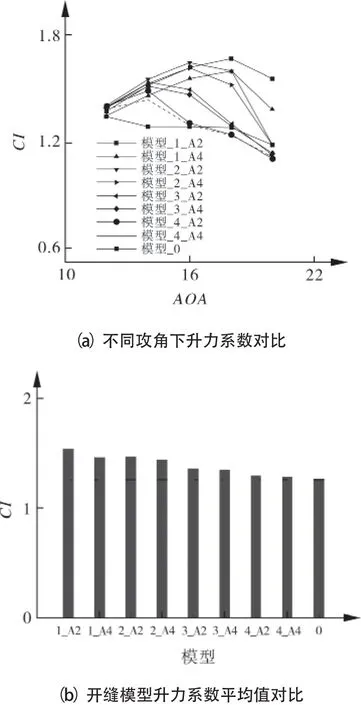
图6 不同模型升力系数对比
图7所示为放大后的不同开缝模型升力系数对比,其中模型_1_A2(x=0.5m)气动性能相对最高,射流位置位于x=0.6 m处的气动性能开始下降,x=0.8 m处性能相对最差,但仍略高于模型_0。从升力系数随攻角的变化可以看出,随着开缝位置后移,其升力系数逐渐下降,静态失速角前移。射流位置在x=0.6 m处的失速角为16°,射流位置在x=0.7 m处的失速角为14°,射流位置在x=0.8 m处其失速角同样也为14°。
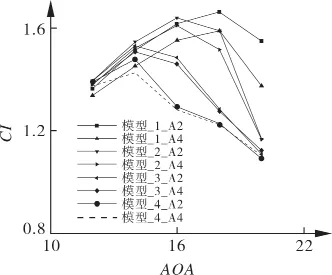
图7 开缝模型升力系数对比
在x=0.5m和x=0.6m采用射流技术后,风力机叶片升力系数提高较为明显,并且在所研究的攻角范围内均优于原型叶片,相比而言,射流角度改变会影响不同模型的静态失速角分布,喷射角度越小,其性能越好。模型_1_A2的最大升力系数为1.66,其失速角为18°;模型_1_A4的最大升力系数为1.59,在攻角为18°出现,较模型_1_A2的最大升力系数小0.07;模型_2_A2的最大升力系数为1.64,在攻角为16°发生,较模型_1_A2的最大升力系数小0.02。模型_2_A2的均值比模型_1_A2小,但略优于模型_1_A2。说明喷射角度的改变在一定条件下可以改善流场。
从图7还可以看出,在位置相同的条件下,不同喷射角度的升力系数变化趋势几乎一致,2°喷射条件下的升力系数要比4°喷射条件下的升力系数总体略高。
图8为18°攻角下典型开缝模型叶片(选取位置为x=0.5 m和x=0.8 m)的流场及压力分布。从图8(a)-(h)可以看出,在加入射流以后,模型_1_A2、模型_1_A4的流动分离得到极大抑制,模型_1_A2的涡漩结构被限制在x=1.0 m的尾缘处,影响区域有限。而模型_1_A4的涡漩结构维持在x=0.7582~1.0 m的范围,分离点位于x=0.7582 m处,该结构会导致流过此处的气体速度降低、压力升高,从而导致升力下降,从数值结果来看,也同样说明这一点,即模型_1_A4的升力系数比模型_1_A2低0.07。模型_4_A2、模型_4_A4的射流位置均位于x=0.8 m,从流场表现来看,漩涡结构影响区域明显扩大,叶背后半部的吸力面上方出现涡旋结构区域,范围在x=0.42~1.2 m之间。分流点大大提前,约在x=0.42 m位置处。从升力系数计算结果分析可得,射流位置位于分流点之后,对改善流场几乎不起任何作用,结合压力分布图,可以看到两者虽然喷射角度不同,但压力分布几乎一样,也说明风力机叶片的分离流对射流位置更加敏感,随着射流起始位置后移,其改善流场状态的能力进一步削弱,涡旋影响区域显著扩大。而喷射角度只会局部改善流动状况。
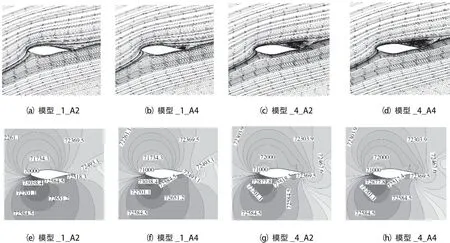
图8 开缝叶片18°攻角下流线及压力对比
图9为18°攻角下开缝叶片与原型叶片的流场分布对比。
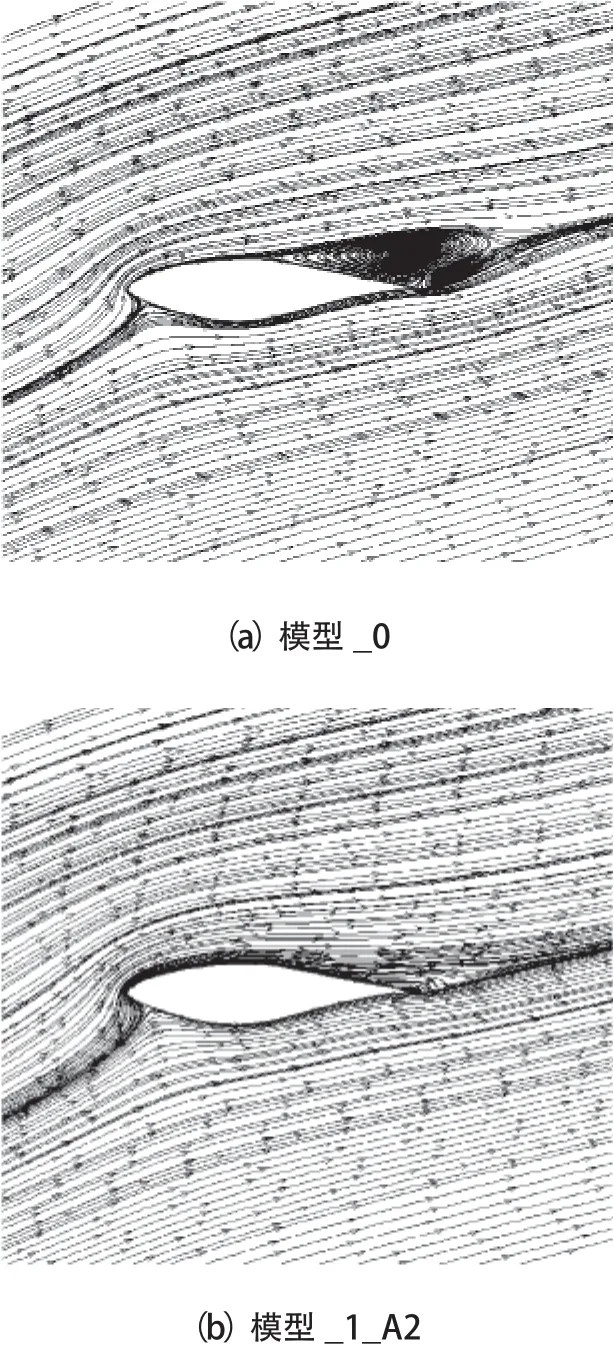
图9 18°攻角下开缝叶片与原型叶片流场对比
从图9可以看出在较大攻角下两种模型的流场区别较大,其中模型_0在叶背后半部出现较大漩涡结构,而模型_1_A2的流动状态得到大大改善,仅在尾缘处出现附着涡,有利于升力系数提高。
图10所示开缝与原型叶片回流区位置流场对比。

图10 18°攻角下开缝叶片与原型叶片回流区位置流场
观察图10(a)、(b)可以发现,射流位置位于回流区内的左侧,该处的高能流体向下游流动并冲击涡旋结构核心,大涡分解为若干小涡,提高流体抵抗逆压力梯度的能力,并减少附面层厚度,达到消除减弱回流区的效果。
图11为18°攻角下模型_0(原型叶片)与模型_1_A2(开缝叶片)压力系数对比,从图11中可以看到在加入射流后,叶片下壁面的压力系数分布差别较小,叶片上壁面的压力系数出现较大不同。原因在于射流出现后,吸力面的流体加速向下游流动,压力变小,从物理角度来看则是“等效”增加了叶片的弯度与环量,起到增升效果。即压力系数曲线所包含的面积增加,升力系数变大。
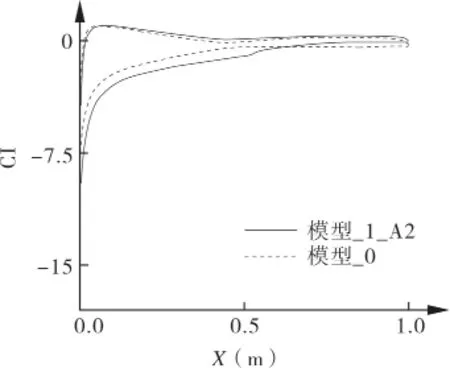
图11 开缝叶片与原型叶片压力系数对比
通过上述分析可以看出:引入高能气流在狭缝出口处形成射流,改善附面层流动状态,下游附面层低能流体可以从射流中获取能量,对大攻角下出现的大尺度漩涡及后缘涡起到一定的削弱和清除作用,提高叶片的气动性能及升力系数。
5 结论
(1)在所研究的攻角12~20°范围内,开缝模型性能均优于原始叶片模型,其中模型_1_A2的气动性能相对最高,其最大升力系数为1.66,其失速角为18°。
(2)大攻角下,射流会减弱并抑制流动分离现象发生。射流位置与改善叶片气动性能密切相关,开缝位置位于x=0.5 m时,气动性能最好,随着后移,其控制效果减弱,越接近尾缘,分离流动控制效果越弱。在分离流动控制有效的条件下,2°喷射角度效果要优于4°喷射角度,但在射流位置靠后的情况下,喷射角度对叶片性能影响较小。
(3)射流可以提高叶片气动性能并改善叶片工作稳定性。高能气体出口处附近形成高速射流,扫掠附面层低能流体,有利于削弱和清除吸力面上的大尺度涡旋结构及尾缘涡、附着涡,有利于风力机机械性能提高。
[1] 中国工程院.中国能源中长期(2030-2050)发展战略研究(可再生能源卷)[M].北京:科学出版社,2011.
[2] 贺德馨.中国风能发展战略研究[J].中国工程科学,2011,13(6):95-100.
[3] 钟伟,王同光.SST湍流模型参数校正对风力机CFD模拟的改进[J].太阳能学报,2014,35(9):1743-1748 .
[4] 周正贵.压气机/风扇叶片自动优化设计的研究现状和关键技术[J].航空学报,2008,29(2):257-266.
[5] Ozgen S,Canibek M.Ice accretion on multi-element airfoils using extended messinger model[J].Heat Mass transfer,2009,45:305-322.
[6] Seifert A,Darabi A,Wygnanski I.Delay of airfoil stall by periodic excitation[J].Journal of Aircraft,1996,33(4):691-698.
[7] Johansen J,Soerensen N N,Peck M,et al.Rotor blade computations with 3D vortex generations[R].Denmark:Risoe National Laboratory,Ris oe-R-1486,2005.
[8] 高翔,胡骏,王志强.叶尖射流对风力机叶尖流场影响的数值研究[J].航空动力学报,2014,29(8):1863-1870.
[9] 金琰,袁新.风力机翼型颤振及射流减振技术的气动弹性研究[J].太阳能学报,2002,23(4):403-407.
[10] 叶建,邹正平,陆利蓬,等.低雷诺数下翼型前缘流动分离机制的研究[J].北京航空航天大学学报,2004,30(8):693-697.
[11] Spalart P,Allmaras S.A One-Equation Turbulence model for Aerodynamic Flows[R].AIAA-92-0439.
[12] Long Wang,Lun-ye Sun,Guang Wu,et al.Research on algorithm of blade vibration for general wind turbine[C].Proc.SPIE9903,Seventh International Symposium on Precision Mechanical Measurements,990325.
[13] 王龙,钟易成,吴晴,等.双锥Bump压缩面设计及气动特性[J].航空动力学报,2013,28(1):82-89.
[14] 王龙,李雪斌,来永斌,等.基于预条件技术的风力机叶片计算方法研究[J].安徽理工大学学报:自然科学版,2016,36(4):47-51.
[15] 谭蔚,晋文娟,吴皓,等.刚性管对正方形排布管束流体弹性不稳定的影响研究[J].压力容器,2016,33(3):1-7.
[16] 葛玖浩,李伟,陈国明,等.基于EN13445直接法的深海外压容器稳定性研究和影响因素分析[J].压力容器,2015,32(2):21-26.
[17] 陈孙艺.压力容器有限元分析建模中值得关注的几个工程因素[J].压力容器,2015,32(5):50-57.
[18] 郭小宝,赵振,陈落根,等.基于能量法的重载码垛机器人重力平衡分析与设计[J].包装与食品机械,2015,33(6):43-46.
[19] Gilarranz J L,Traub L W,Rediniotis O K.A New Class of Synthetic Jet Actuators—Part II:Application to Flow Separation Control[J].Journal of Fluids Engineering,2005,127(2):377-387.

