基于流固耦合的接触式机械密封端面泄漏率的研究

张 鹏，李双喜，王 梁，蔡纪宁

（北京化工大学，北京 100029）

1 前言

准确地计算机械密封端面泄漏率，并分析其影响因素是研究釜用机械密封失效机理的关键。采用经验公式计算接触式机械密封端面泄漏率没有考虑密封端面变形，存在较大的误差［1］。

目前，考虑密封端面变形并对密封端面间隙和泄漏率进行数值计算方面，已经得到了一些成果。采用数值计算的方法，可以优化密封设计，预测机械密封的性能［2～10］。张绪猛等建立了考虑机械密封端面粗糙度及其摩擦生热作用的数学模型，计算结果表明密封端面液膜厚度由内 向外逐渐变大［11］。杨惠霞等提出的混合摩擦机械密封模型，可以预计同时考虑表面粗糙度、周向波度和径向锥度等作用的密封特性［12］。孙见君等得到了密封端面形貌变化与机械密封泄漏率之间的关系，以及泄漏率与时间的关系［13］。

本文在前人研究的基础上，提出考虑密封环端面受力变形影响的接触式机械密封端面泄漏率数值计算模型，并利用ANSYS和MATLAB软件对密封端面泄漏率进行流固耦合数值求解。

2 密封端面泄漏率数值计算模型

2.1 考虑粗糙度的密封端面流体计算模型

接触式机械密封在使用过程中，其密封端面微凸体接触状态如图1所示。

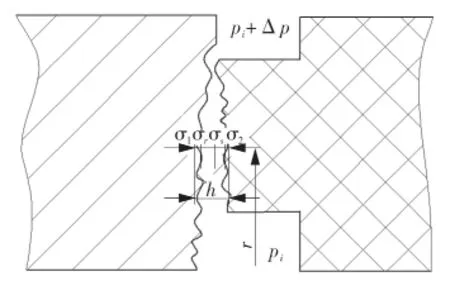
图1 密封端面微凸体接触状态

引入无量纲参数压差流量因子φr，得到考虑密封环表面粗糙度影响密封端面流体流 动雷诺方程［14］：

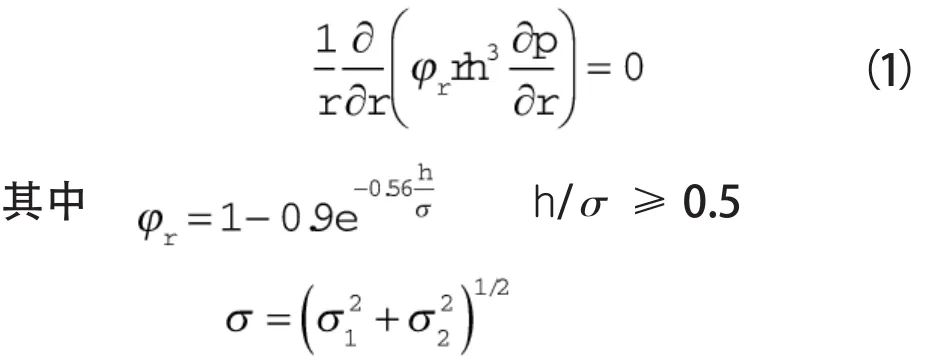
式中 r ——密封端面任意处的半径，mm

h ——密封端面间隙，mm

p ——密封端面任意处压力，MPa

σ——密封端面综合表面粗糙度，mm

σ1，σ2—— 动、静环表面的轮廓算术平均偏差，mm

2.2 密封端面间隙计算方法

稳定工作状态下，机械密封浮动环的受力满足载荷平衡条件：

稳定工作状态下，密封闭合力Fclose由密封介质压力、弹簧力和密封载荷比共同确定。一般接触式机械密封不考虑密封端面的动压效应，Fopen由端面液膜压力p提供，端面接触力Fc由端面接触压力pc提供。

p，pc与h存在耦合关系，先确定h值的大小。h是由密封端面形貌决定的基本间隙与动、静环端面的变形共同确定的，其表达式为：

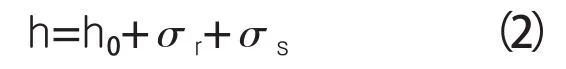
式中 h0——密封端面的基本间隙，mm，取h0=σ

σr—— 动环端面任意半径处变形值，mm

σs—— 静环端面任意半径处变形值，mm

考虑密封环整体变形影响，密封端面变形值按以下方法确定：通过ANSYS软件建立密封动、静环接触模型，再施加相应的载荷和约束条件进行求解，从而得到摩擦副端面的接触变形状态。提取动环和静环端面节点处的轴向位移，即为动环、静环密封端面在该半径处的变形大小。

2.3 基于流固耦合密封端面泄漏率计算程序

忽略惯性效应，在求得密封端面液膜压力分布和间隙分布后，即可求解密封端面任意半径处的体积泄漏率 Q［10］：

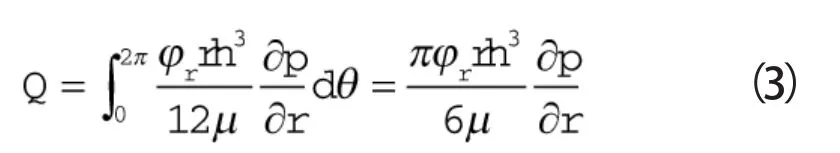
密封端面间隙h会影响密封端面间的压力p分布，端面压力p的分布又会影响到密封端面间隙h。根据以上耦合模型，得到接触式机械端面泄漏率的计算程序如图2所示。

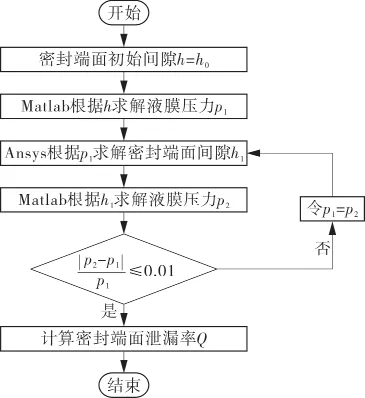
图2 密封端面泄漏率计算程序

2.4 密封端面泄漏率计算模型

本文以某型号釜用机械密封为例进行研究，该型号机械密封运转状态良好稳定，密封结构如图3所示。

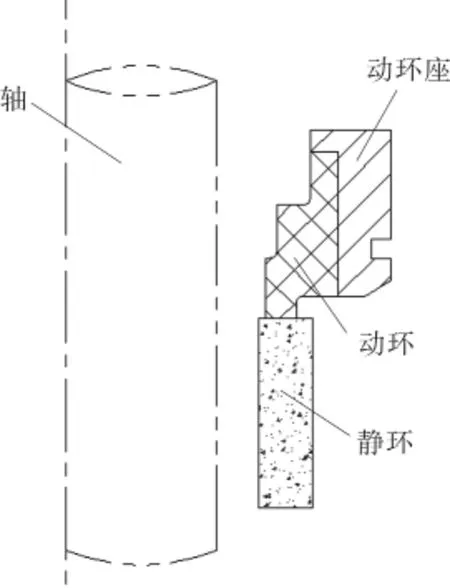
图3 密封摩擦副结构

本文采用的机械密封模型中，密封副材料特性如表1所示，各影响因素取值如表2所示。

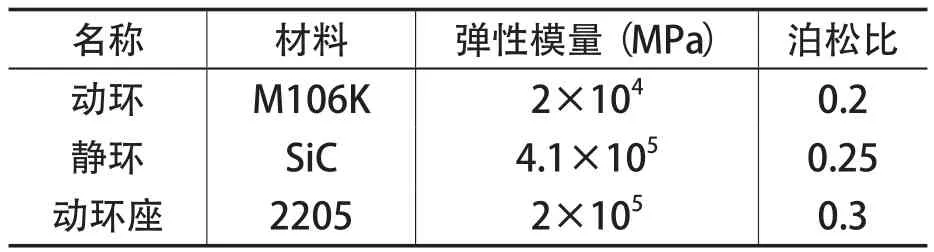
表1 材料特性

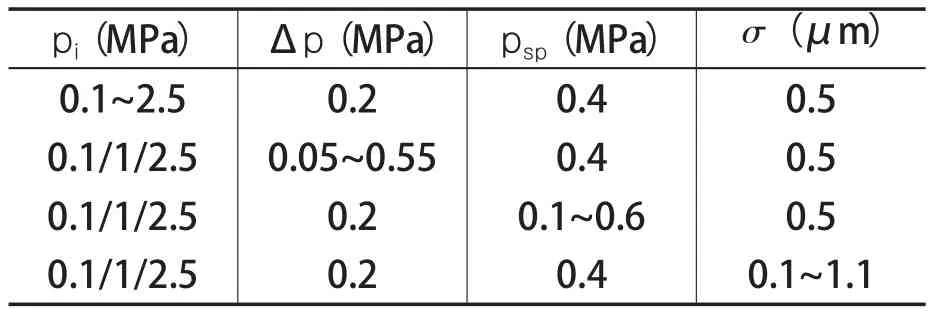
表2 影响参数值

建模时，忽略对整体结构影响甚微的传动槽等结构，则该机械密封摩擦副具有轴对称特征。在保证求解精度和求解效率的前提下，利用ANSYS软件建立二维平面模型，单元类型选用PLANE42单元。动环和静环、动环和动环座之间建立接触对。网格均采用四边形扫略划分，且经网格无关性验证，网格数为1.2万。

密封摩擦副有限元模型如图4所示。密封端面接触状态如图5所示。可以看出，密封端面间的实际接触主要发生在靠近密封端面外侧区域；迭代耦合求解后，密封端面间液膜压力分布受密封端面接触状态的影响，液膜压力由内侧到外侧加速增大。

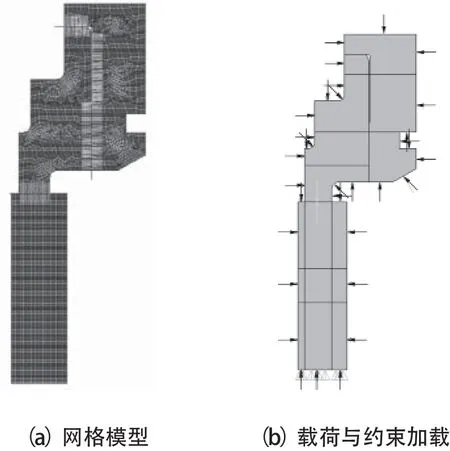
图4 密封摩擦副有限元模型

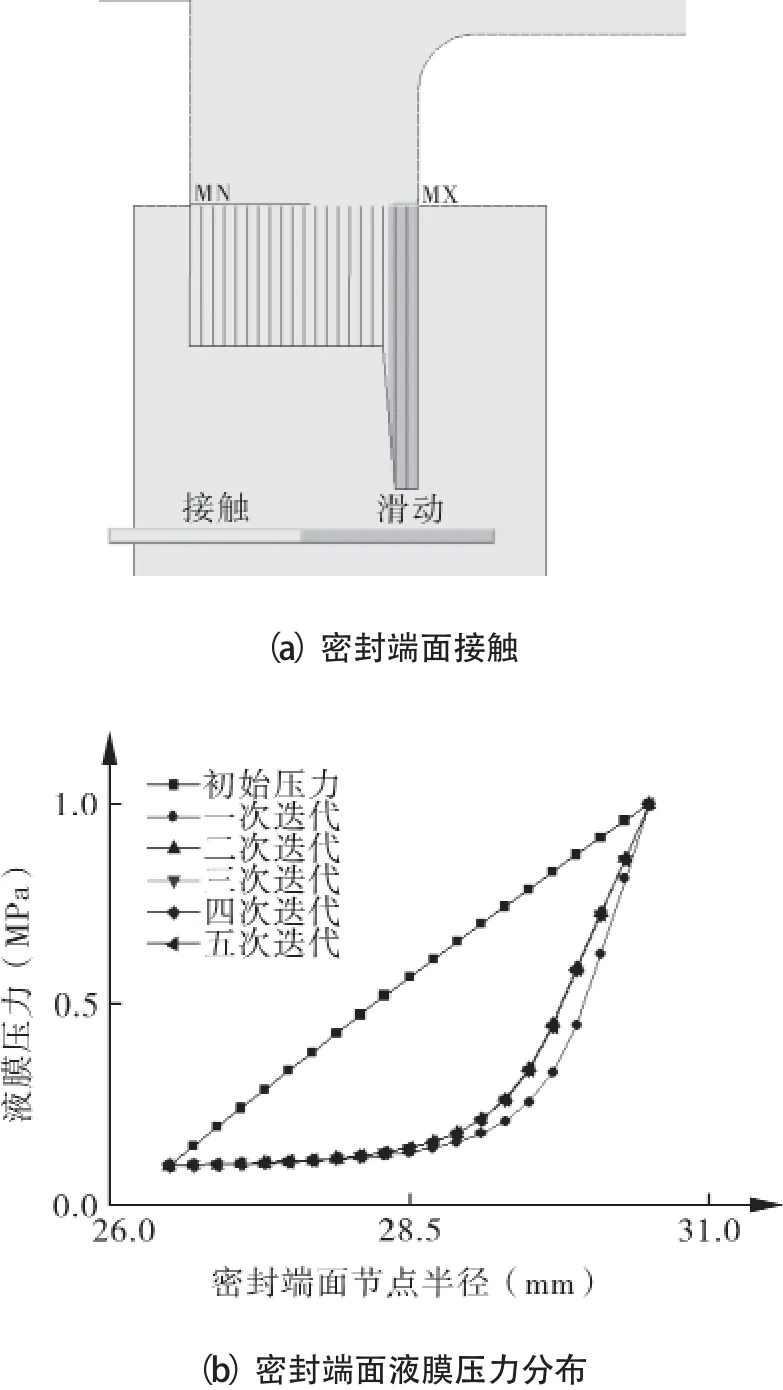
图5 密封端面接触状态与液膜压力分布

3 密封端面泄漏率影响因素分析

密封端面间隙h由密封端面基本间隙h0及动、静环端面变形值决定，而动环和静环的端面变形受到密封介质压力、弹簧比压及密封端面压差的共同影响；密封端面基本间隙h0取决于密封端面综合表面粗糙度。本节将研究以上参数对密封端面泄漏率的影响规律。

3.1 密封介质压力对端面泄漏率的影响

根据泄漏率的计算方法及表2中的参数，计算密封端面泄漏率Q随密封介质压力pi的变化情况，结果如图6所示。

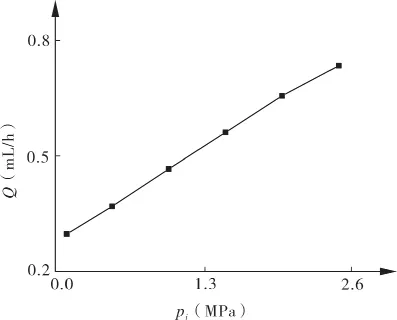
图6 密封端面泄漏率随pi的变化规律

由图可知，密封介质压力越大，密封端面泄漏率越大，且其与密封介质压力近似呈一次线性关系。可见，在使用密封介质压力范围内，密封端面泄漏率维持在较低的水平，密封介质压力并不会直接造成密封端面过量泄漏。

3.2 密封端面压差对端面泄漏率的影响

根据泄漏率的计算方法及表2中的参数，计算不同密封介质压力下，密封端面泄漏率Q随密封端面压差Δp的变化情况，结果如图7所示。

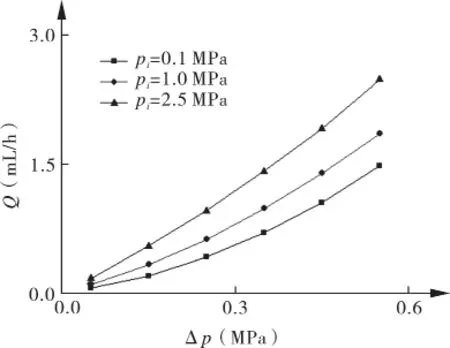
图7 密封端面泄漏率随Δp的变化规律

从图可以看出：密封压差越大，密封端面泄漏率越大，且泄漏率增加速率加快。密封介质压力越大，密封压差对端面泄漏率的影响越大。因此，当密封介质压差过大时，过大的密封压差将有可能导致密封端面过量泄漏。

3.3 弹簧比压对端面泄漏率的影响

根据泄漏率的计算方法及表2中的参数，计算不同密封介质压力下，密封端面泄漏率Q随弹簧比压psp的变化情况，结果如图8所示。

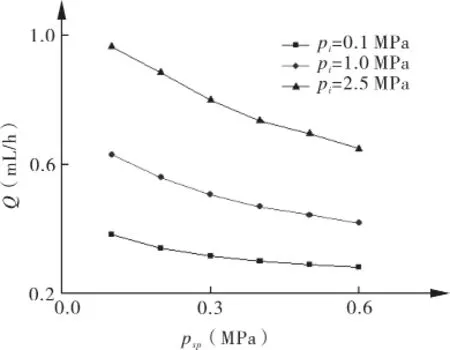
图8 端面泄漏率随psp变化规律

从图可以看出：随着弹簧比压的增大，密封端面泄漏率减小且趋于稳定。弹簧比压对端面泄漏率的影响较小，随着弹簧比压的增大，对泄漏率的影响会趋于稳定。可见，正常工作情况下，由于弹簧比压的改变引起端面过量泄漏的可能性较小。

3.4 密封端面综合表面粗糙度对端面泄漏率的影响

根据泄漏率的计算方法及表2参数值，计算不同密封介质压力下，密封端面泄漏率Q随密封端面综合表面粗糙度σ的变化情况，结果如图9所示。

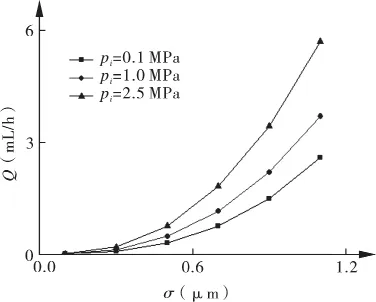
图9 密封端面泄漏率随σ变化规律

从图可以看出：密封端面综合表面粗糙度越大，密封端面泄漏率越大，当密封端面综合表面粗糙度超过0.5 um后，泄漏率增加速率明显加快。密封介质压力越大，密封端面综合表面粗糙度对端面泄漏率的影响越大，即使在密封介质压力较小的情况下，较大的密封端面粗糙度会导致端面过量泄漏。

4 计算结果试验验证

根据经验公式计算机械密封端面体积泄漏率［14～16］：

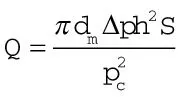
式中 dm——密封端面平均直径，mm

Δp——密封流体压差，MPa

S——间隙系数

pc——密封端面比压，MPa

介质压力pi、密封端面压差Δp、弹簧比压psp和密封端面综合表面粗糙度σ等参数值如表3所示。

表3 试验参数

不同阻封液压力下，密封端面泄漏率理论值与试验值的对比如图10所示。

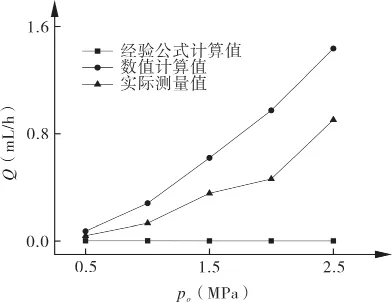
图10 密封端面泄漏率计算值与试验值

从图可以看出，数值计算值稍大于实际测量值，且随着压力的增加，误差稍有增大，这是受到了试验件本身加工误差及试验误差等因素综合作用的影响。数值计算值偏大的原因在于，采用压力流量因子φr对密封端面流体润滑雷诺方程进行修正，得到的考虑密封端面粗糙度的润滑模型也存在一定的误差。

相比于密封端面泄漏率的经验计算值，数值计算值与实际测量值的误差更小，而且 数值计算值更准确反应了密封端面间隙和泄漏率随阻封液压力的变化规律。因此，采用数值计算方法对密封端面泄漏率的影响因素及其影响规律进行研究是可行的。

5 结论

（1）基于流固耦合的密封端面泄漏率数值模拟值比经验公式计算值更接近测量值，且能准确反应密封端面间隙和泄漏率随阻封液压力的变化规律。

（2）端面泄漏率与密封介质压力近似呈一次正比例线性关系。密封介质压力在使用范围内，不会直接造成密封端面过量泄漏。

（3）端面泄漏率随密封压差的增大而加速增大，且对端面泄漏率的影响随着密封介质压力的增大而增大。随着密封压差的增大，有可能导致密封端面过量泄漏。

（4）端面泄漏率随弹簧比压的增大而减速增大，弹簧比压对端面泄漏率的影响较小，由于弹簧比压的改变而引起端面过量泄漏的可能性较小。

（5）端面泄漏率随密封端面综合表面粗糙度的增大而加速增大，且其对端面泄漏率的影响随着密封介质压力的增大而增大，较大的密封端面粗糙度易导致端面过量泄漏。

［1］ 魏龙，常新中，张鹏高.接触式机械密封端面泄漏模型的研究进展［J］.流体机械，2012，40（2）：36-40.

［2］ Meck K D，Zhu G.Improving mechanical seal reliability with advanced computational engineering tools，part 1：FEA［J］.Sealing Technology，2008（1）：8-11.

［3］ Meck K D，Zhu G.Improving mechanical seal reliability with advanced computational engineering tools，part 2：CFD and application examples［J］.Sealing Technology，2008（2）：7-10.

［4］ 葛培琪，陈利海，程建辉，等.考虑表面粗糙度和径向锥度的机械密封混合摩擦计算模型［J］.润滑与密封，2001（5）：14-16.

［5］ 丁雪兴，程香平，李国栋，等.机械密封混合摩擦微极流场数值模拟［J］.石油化工高等学校学报，2008（2）：63-67.

［6］ 於秋萍，孙见君，涂桥安，等.接触式机械密封基本性能研究进展 ［J］.流体机械，2015，43（2）：41-47.

［7］ 王彬，程旼.炼油装置中几种典型泵用机械密封及系统选型分析［J］.化工设备与管道，2015，52（4）：44-47.

［8］ 彭常飞，张志强，赵振兴，等.整体式绝缘接头密封性能和强度研究［J］.压力容器，2015，32（5）：58-63.

［9］ 陈汇龙，左木子，吴强波，等.上游泵送机械密封润滑膜固液两相流动特性［J］.排灌机械工程学报，2015，33（8）：685-690.

［10］ 王乐勤，孟祥铠，戴维平，等.接触式机械密封流固耦合模型及性能分析［J］.工程热物理学报，2008（11）：1864-1866.

［11］ 张绪猛，朱汉华，范世东，等.基于MATLAB的混合摩擦工况下机械密封动态特性研究［J］.润滑与密封，2008（10）：27-30.

［12］ 杨惠霞，顾永泉.考虑微凸体塑性变形的接触式机械密封混合摩擦特性计算［J］.石油化工设备，1998（4）：29-32.

［13］ 孙见君，顾伯勤，魏龙.基于分形理论的接触式机械密封泄漏模型［J］.化工学报，2006（7）：1626-1631.

［14］ 顾永泉.机械端面密封［M］.东营：石油大学出版社，1994.

［15］ 周辉，文卫朋，尚庆军.双金属自密封波齿垫片结构参数及密封性能研究［J］.压力容器，2015，32（4）：16-21.

［16］ Mayer E，著.姚兆生，许仲枚，王俊德，译.机械密封［M］.北京：化学工业出版社，1981.