侧入式单端面机械密封摩擦副温度场的研究

孙星星，孟祥铠，周国忠，虞淑瑶，赵文静

（1.浙江工业大学过程装备及其再制造教育部工程研究中心，浙江杭州 310032；2.浙江长城搅拌设备股份有限公司，浙江温州 325028）

1 前言

侧入式单端面机械密封是火电厂烟气脱硫吸收塔搅拌混合系统的关键密封设备。其机械密封摩擦副工作时，动、静环端面之间相互贴合紧密且相对转动，摩擦副之间由于介质压力及摩擦力作用会产生磨损和热量，加之此类典型结构机械密封腔体狭小，散热性能差，从而导致产热量大，引起密封环端面温升明显［1，2］。若温升持续增加还会引起摩擦副端面间液膜汽化、磨损加剧、密封环变形，造成机械密封工作不正常，并最终导致端面密封失效。因此，为了提高烟气脱硫吸收塔侧入式搅拌器密封装置端面密封设计质量，需对此类典型结构端面密封摩擦副温度场进行分析计算，以便及时调整设计参数，使得端面温升控制在正常工作范围内，对延长密封装置的使用寿命具有重要意义［3］。

目前，大部分研究者普遍采用商用软件对温度场进行求解［4～6］，且大都认为密封面平行，不考虑热、力变形对温度分布的影响［7～9］，忽略端面间流体黏度随温度的变化，这给密封端面热特性等密封性能的预测带来误差。

本文作者综合考虑密封动静环热力变形、润滑液膜压力分布和液膜黏温特性间的耦合关系，建立机械密封轴对称模型，采用整体接触耦合法和相关数值计算手段实现理论模型的数值求解，得到密封环的温度场分布，并通过自主设计的密封试验台进行验证。

2 机械密封环的几何模型与前提假设

2.1 几何模型

因为密封环呈轴对称结构，可采用如图1所示的密封环纵截面为所研究问题的几何模型，该模型包括静环、动环和端面间的一层液膜。作为浮动环的静环不应添加轴向约束，而动环底部给定轴向位移约束。图中Ri，Ro，Rb分别为密封环内径、外径和平衡半径。本文几何参数为：Ri=56.5 mm，Ro=60.5 mm，Rb=57.5 mm，平衡比为0.7564。

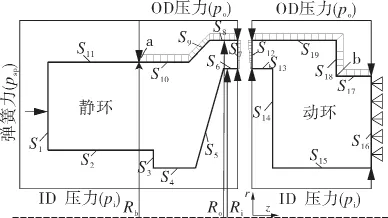
图1 密封环几何模型及边界条件

密封静环力的边界条件：静环底部受到内压pi作用，同时还受到弹簧力Fs的作用，边界S1～S6和S11均受内压pi作用，外径侧O型密封圈处（如图1中a）及其右侧边界S8～S10均受密封介质压力po作用，静环密封端面部分受液膜压力p的作用。

密封动环力的边界条件：动环底部给定轴向位移约束条件，边界S13～S15均受内压pi作用，外径侧O型密封圈处（如图1中b）及其左侧边界S17～S19均受外压po作用，动环密封端面部分受液膜压力p的作用。

2.2 密封环热分析的基本假设

由于机械密封装置实际工况的复杂性，考虑的因素越多不仅会增加运算量，还可能降低方程的可求解性，因此对一些次要或不确定因素做相应简化处理是很必要的，综合上述的建模思路和相关分析理论，现对计算模型做如下假设：

（1）机械密封环的计算模型是轴对称的，即密封环的尺寸形状和所受载荷都为轴对称，且不随时间变化；

（2）密封环为理想弹性体，即密封环的材料是均匀连续、各向同性和完全弹性的；

（3）动、静环端面间液膜厚度很薄，忽略端面间液膜的对流换热作用，仅考虑动、静环内外侧与相应介质接触边界上的对流换热作用；

（4）密封端面处于混合摩擦状态，液膜黏性剪切和微凸体接触摩擦产生的热量全部由密封环导出到外部介质中，不计搅拌产生的热量及泄漏液体带走热量的影响；

（5）密封端面间的介质温度、黏度沿径向发生变化，沿膜厚方向不变，且密度视为常数；

（6）分析时将动、静环作为一个整体来考虑，避免密封环间的热量分配比的计算。

3 边界条件的确定

3.1 主要参数

密封介质性质、密封工作参数和密封材料的物性参数对机械密封温度场的分布有着重要影响。本文算例的密封工作参数为：主轴转速315r/min，弹簧比压0.2 MPa，密封介质压力0.3 MPa，密封介质为常温清水，初始温度为27 ℃。密封环材料属性见表1，密封介质性能参数见表2。

表2 清水介质27℃时的性能参数

3.2 润滑方程

针对密封端面形成的环向液膜，建立极坐标系下的Reynolds方程：

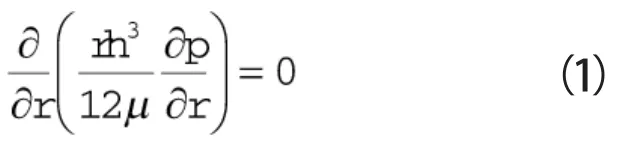
式中 r——流体膜径向坐标，m

h——流体膜厚，m

μ——流体膜黏度，Pa·s

p——液膜压力，MPa

3.3 密封环热传导微分方程

基于文中的基本假设，密封环的传热问题简化为二维问题，稳态条件下，动静环柱坐标下的热传导方程为［10］：

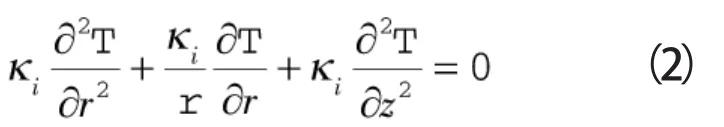
式中 T——密封环内的温度分布，℃

κi——密封环材料的导热系数，W/（m·℃）

z——流体膜轴向坐标，m

为得到方程（2）的唯一解，需要添加相关边界条件，图1表示的为密封环各边界，其中S1～S6、S8～S11、S13～S15、S17～S19采用对流换热边界条件，即第三类边界条件：

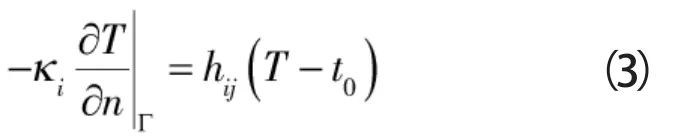
式中 hij—— 密封环空气侧和介质侧的对流换热系数，W/（m2·℃）

t0——密封环参考温度，℃

S7和S12采用热流边界条件，即第二类边界条件：

式中 q——端面摩擦生热，W/m2

当边界处的热流密度为0，则称之为绝热边界条件，S16设为绝热边界条件。

3.4 摩擦热的计算［11］

密封环温升来自于端面摩擦生热q，主要包括流体液膜的黏性剪切热流密度qv和端面微凸体接触摩擦热流密度qf。

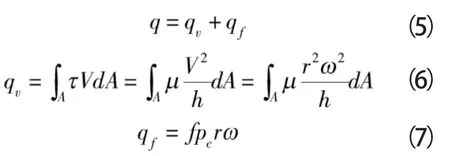
式中 V——动环线速度，m/s

A——密封环端面面积，m2ω——动环角速度，rad/s

f——密封端面干摩擦系数

pc——密封端面的接触压力

任意半径处，接触压力pc可由下式确定：

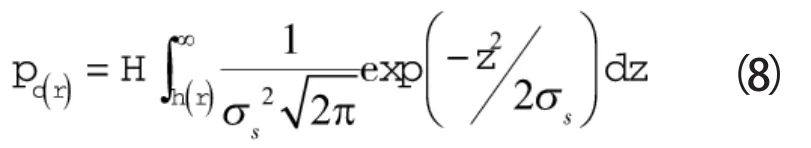
式中 H——软环材料的屈服强度，MPa

σs——密封端面粗糙度标准偏差，μm，取σs=0.106μm

对流体进行热分析时，通常采用的黏度方程为［11］：

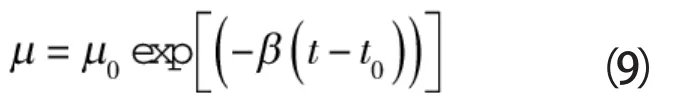
式中μ0——参考温度t0下的黏度，Pa·s

β——黏温系数，1/℃，取β=0.0175/℃

t——端面液膜温度

考虑密封端面的热力变形，流体的膜厚方程为［10］：

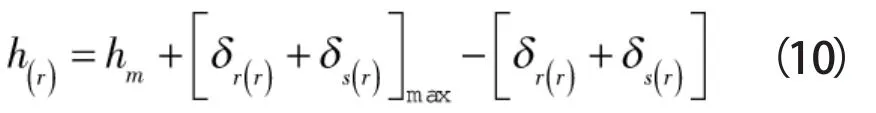
式中 h（r）——不同半径处的膜厚，m

hm——密封端面最小膜厚

δr（r），δr（r）——不同半径处动、静环端面绝对变形量，m

r——下标，动环

s——下标，静环

变形前后相比拉伸为正，压缩为负，［δ1（r）+δ2（r）］max为动静环绝对变形的最大代数和。

3.5 对流换热系数的计算

密封环的摩擦热主要由动环和静环与密封介质和空气的对流换热作用导出，因此对流换热系数是影响密封环温度场分布的一个重要因素。但是，对流换热的计算非常复杂，本文采用以下公式进行处理［12］。

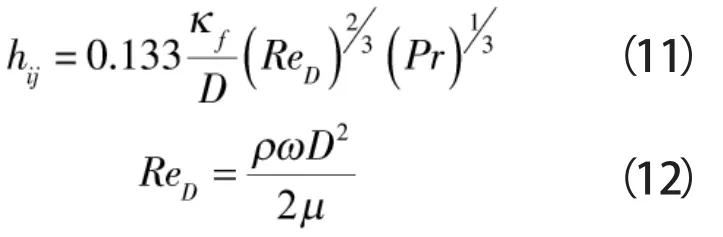
式中 ReD——密封介质的雷诺数

κf——密封介质热传导系数，W/（m·℃）

D——动环外径，m

Pr——普朗特数

ρ——密封介质的密度，kg/m3

ω——主轴的角速度，rad/s

μ——密封介质的动力黏度，Pa·s

cp——密封介质的比热容，J/（kg·℃）

4 计算流程及结果讨论

上述方程采用有限单元法进行求解，计算流程如图2所示，包含以下循环：第1个循环为膜厚的松弛迭代，可通过雷诺方程和热传导方程求解端面压力分布、密封环温度分布；第2个循环为力平衡循环，用于调整最小膜厚，直至力平衡收敛；第3个循环为温度场循环，调整液膜黏度与温度间的耦合关系。其中εh为收敛因子，本文取1.0×10-3。图3所示为转速n=315 r/min介质压力po=0.3 MPa，弹簧比压psp=0.2 MPa时的温度分布云图及端面温度沿径向变化的局部放大，其温度大小沿内径向外径处逐渐增大。图4所示为不同工况下端面温度沿径向的变化，由图4可以看出：随弹簧比压、介质压力和转速的增加，端面温度沿径向的变化趋势一致，其大小近似呈线性增加，且端面温度不均匀性增加。

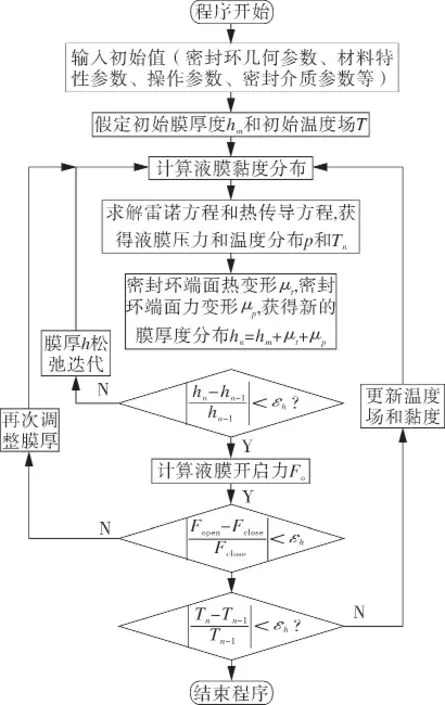
图2 稳态耦合场计算流程

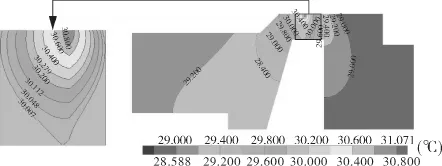
图 3 n=315 r/min，po=0.3 MPa，psp=0.2 MPa 时密封环温度分布云图

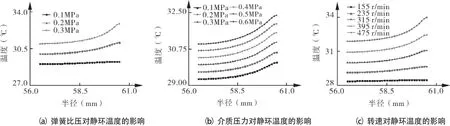
图4 不同工况下端面温度沿径向的分布

5 机械密封环温度测试

5.1 试验装置

试验是在自主设计安装的试验台上进行的，其试验装置原理如图5所示。试验台的动力由1.5kW的直流调速电机提供，主轴转速可通过变频器在0～945 r/min范围内无级调节。介质增压装置主要通过氮气瓶实现且通过稳压阀门进行保压处理，压力调节范围为0～2.5 MPa。弹簧比压的大小改变是通过旋转可调节螺栓实现的，在密封压盖上均布3只可调节螺栓，通过推环作用在弹簧上，从而达到改变弹簧的压缩量，进而调整密封端面的弹簧比压。

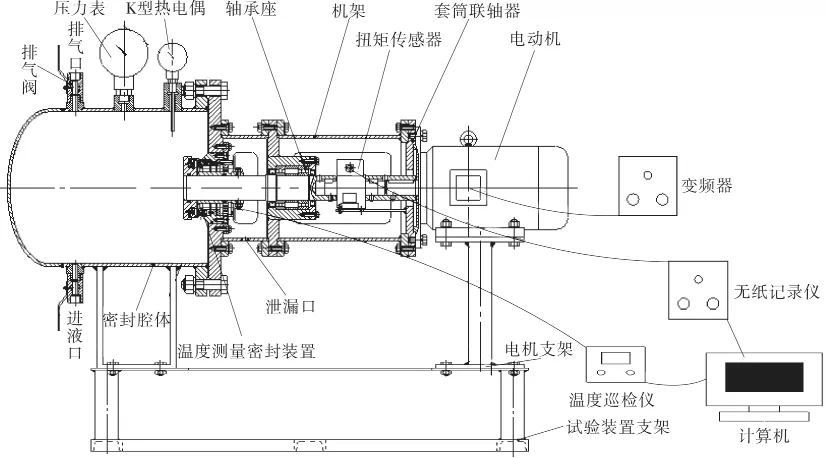
图5 密封试验台工作原理示意

试验中使用的测温传感器为丝径为0.8 mm的K型热电偶，测量所用的热电偶温度传感器探头粘贴在静环内侧靠近端面处，为了提高测量精度，沿周向均布3个温度传感器（如图6，测温点 1，2，3），取平均值。此外，为了探究静环轴向的温度分布情况，沿静环等直径点处分别距离密封端面12 mm（如图6，测温点4）和22 mm（如图6，测温点5）位置点粘贴2个热电偶丝同时进行温度测量。采用SH-X多路温度巡检仪进行采集、显示及存储，温度巡检仪最小刻度为0.1 ℃，最小采样间隔为1 s。

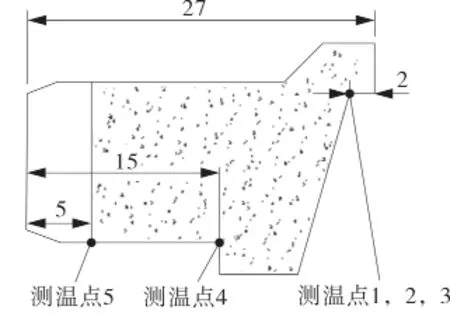
图6 静环中热电偶分布

5.2 分析与结论

图7（a）、（b）、（c）所示分别为各测点温度随弹簧比压、介质压力及转速的变化曲线对比。

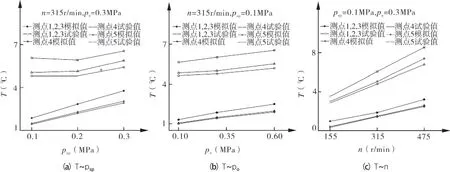
图7 各测点温升随弹簧比压psp、介质压力po及转速n的变化曲线对比

从图可以看出：密封静环端面的温升随弹簧比压、介质压力和转速的增加近似呈线性关系，因为介质压力和弹簧比压的增加使得密封端面比压增加，端面贴合力增大，端面间的润滑介质相对变少、液膜厚度相对减小，导致摩擦副端面微凸体接触面积增大，摩擦力增大，端面摩擦热增加，温度就越高；转速增加，端面平均滑动速度增加，虽然对流换热作用随之加强，但摩擦热的增加是主要因素，结果使端面温度升高。密封静环各测点温度测量值与模拟值在趋势上是一致的，均随着弹簧比压、介质压力和转速的增加而增加，但各测点温度试验值明显大于模拟值。产生误差的主要原因如下：

（1）为了简化计算流程，模拟计算所设置的各热边界条件与实际情况有所偏差，各边界热传导系数主要基于经验公式确定，这也会产生误差。

（2）模拟计算中，端面的热量主要由接触摩擦热和液膜的黏性剪切热组成，没有考虑搅拌热的影响，这也是导致试验值偏大的原因。

（3）密封环导热系数的选取与实际有所偏差，温度测量仪表的零漂以及热电偶从静环上导出部分热量等因素，也会导致试验值与模拟值存在误差。

6 结论

（1）采用整体接触耦合法对烟气脱硫用侧入式单端面机械密封装置摩擦副温度场进行稳态分析，获得了机械密封的温度分布。密封环最高温度出现在靠近介质侧的端面外径处且沿外径至内径逐渐降低。

（2）密封静环端面温度随弹簧比压、介质压力和转速的增加近似呈线性关系，且各测点温度测量值与模拟值在趋势上基本一致。文中所介绍的计算密封环温度分布的方法可行，可为进一步研究此类典型结构密封环的热特性提供参考。

［1］ 蔡晓君，徐旭康.侧开孔式搅拌器密封的设计［J］.流体机械，2000，28（8）：18-20.

［2］ 李小莉.水平侧入式搅拌器机械密封损坏原因分析及改造［J］.流体机械，2003，31（6）：33-34+47.

［3］ 程建辉，陈利海，葛培琪.机械端面密封计算技术［J］.润滑与密封，2001（6）：9-11.

［4］ 王隽，王娟，周旭辉，等.船舶艉轴密封装置端面密封摩擦副温度场稳态分析［J］.润滑与密封，2007，32（7）：122-125.

［5］ 楼建铭，孟祥铠，李纪云，等.波度端面机械密封温度场的有限元分析［J］.流体机械，2015，43（9）：15-21.

［6］ 陈汇龙，彭正东，丁郁华，等.基于ANSYS的大型艉轴机械密封环温度场理论研究［J］.润滑与密封，2010，35（10）：73-76.

［7］ 彭旭东，谢友柏，顾永泉.机械密封端面温度的确定［J］.化工机械，1996（6）：25-28.

［8］ 宫晓清，孟祥铠，李纪云，等.核主泵用流体动压型机械密封温度场的数值研究［J］.流体机械，2015，43（7）：16-21.

［9］ 周剑锋，顾伯勤.机械密封环的传热特性分析［J］.机械工程学报，2006，42（9）：201-206.

［10］ 高斌超，孟祥铠，李纪云，等.机械密封热力耦合有限元模型与密封性能分析［J］.摩擦学学报，2015，35（5）：550-556.

［11］ Ruan B O，Salant R F，Green I.A mixed lubrication model of liquid gas mechanical face seals［J］.Tribology Transactions，1997，40（4）：647-657.

［12］ Djama☒ A，Brunetiere N，Tournerie B.Numerical modeling of the thermohdrodynamic mechanical face seal［J］.Tribology Transactions，2010，53（3）：414-425.