吃不完的巧克力

吴朝阳

我们先来说一件趣事。比利时布鲁日市有一个巧克力名牌叫“The Chocolate Line”，它有一款供多人分享的巧克力，是5×13小块的长方形，如图1。

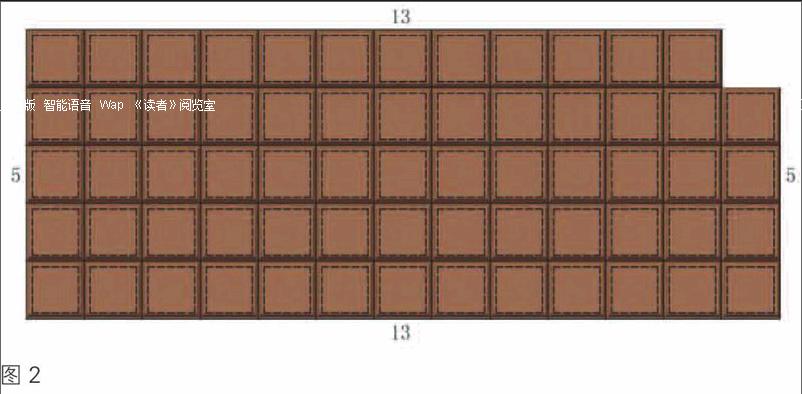
有一天，中学数学教师马蒙（P.Mammone）买了一块这样的巧克力，准备带到课上给学生分享。在拿出巧克力的瞬间，马蒙突然发现他可以做一件有趣的事情。于是，他拿出这块巧克力，掰下右上角的一小块吃掉，把剩下的部分画在了黑板上（图2）。

接着，他把黑板上的巧克力分成3部分（图3）

然后移动拼接成为8×8的正方形（图4）。

接下来，他又把这个正方形分成4块（图5），拼接成了5×13的长方形（图6）。

这样，马蒙老师把一块5×13的巧克力吃掉了1个小单元，最后又拼成了原来的5×13的形状。吃了等于没吃？所以这块巧克力会永远吃不完？演示完毕，马蒙老师把真正的巧克力分给他的学生，然后向他们提出问题——黑板上这“吃不完的巧克力，到底是怎么回事？

学生们二二两两地喃咕着，但好久都没有发现问题。于是，马蒙老师说，大家都习惯于“眼见为实”，虽然明摆着与常识不符，却迷惑于眼睛所见，不能很快发现问题的所在。

事实上，我们首先清楚，8×8=64，5×13=65，因此最后一个拼接肯定是错误的。那么，错误产生在什么地方呢？我们看到，所有直角边的边长，即3、5、8这些数字，衔接得毫无问题，而直角之间的衔接自然也都天衣无缝。因此，问题肯定出在斜线上！

马蒙老师接着说，理性让我们很快发现问题出在斜线上，剩下的事情就简单了，我们马上进行计算——三角形上斜边的斜率是3/8=0.375，而梯形上则是2/5=0.4，二者并不相等！换句话说，梯形和三角形拼接出来的形状，其“斜线”不是直线！实际拼接出来的图形是这样的（图7）。

它的中间有一条很细的缝！马蒙老师接着说，现在，不用计算大家都知道，这条缝的面积肯定恰好等于1小块巧克力的大小！

这个故事告诉我们理性分析的重要性，没有理性的支撑，则“眼见”未必“为实”。然而，故事的背后有一個非常重要的事实，就是：

事实：移动平面几何图形并不会改变它的面积。两个平面几何图形拼接成的图形，其面积等于原来那两个图形的面积之和。

上述这条事实是很多几何证明的基础。例如，大家所熟知的勾股定理，它的很多种证明就都应用了上述事实。比方说，勾股定理的如下证明，它唯一用到的就是上述事实。

大家都知道，长方形的面积等于它的长乘以宽，但是，大家有没有想过它是怎么来的？事实上，如果我们将边长等于1长度单位的正方形（即单位正方形）的面积定义为1（面积单位），那么长方形的面积公式是可以由这个定义出发证明的。

首先，我们考虑边长分别为1和1.1的长方形，它的面积是多少呢？显然，这个长方形的长可以分为11个0.1，宽可以分为10个0.1。因此，这个长方形可以分割成110个边长为0.1的小正方形。而100个这种小正方形正好可以拼成1个单位正方形。根据分割的形式，我们不难得到结论：这个长方形的面积等于它的长乘以宽，即l×1.1。

循着这种思路，我们不难证明：边长是有理数的长方形的面积等于它的长乘以宽。而对于某边长等于无理数的情形，只要我们具备极限的概念，公式的成立也是顺理成章的事情。显然，除了极限的思想，长方形面积公式的证明，同样只依赖于前述事实。

最后我们指出，前述事实自古以来就在几何证明中扮演着最关键的角色。在古代中国，它体现为“出入相补原理”。这条原理的名称毋须多加解释，而根据这条原理，大家可以很快地自行推导出平行四边形、三角形、梯形等平面图形的面积公式，甚至常见立体的体积公式，从未自己推导过的小读者不妨立刻动手尝试。endprint