核心问题引领：小学数学对话教学的理性追求

王 玉 东

(海安县明道小学，江苏 海安 226600)

心理学家马秋斯金认为，对话的最基本结构是“问题—问答”……人正是凭借问题吸引他人对自己的注意。保罗·弗莱雷认为，对话是教育的主要途径之一，要使对话有成效，提问是关键；他认为，教师不应只是知识的传递者，而更应成为问题的提出者。伽达默尔同样认为，对话以“提问问答”的方式进行[1]。可见，问题是数学对话教学的引擎和动力，问题的好差直接影响数学课堂质量的优劣。但审视现状，低质量的问题仍充斥着课堂，数学对话的去思维化明显，看似热闹非凡，实则虚假繁荣。

一、理性追问：为何提出基于核心问题的小学数学对话教学

1.问题的零散性

数学是一门逻辑性很强的学科，它遵循着知识发生、发展的脉络。在不少课堂上，教师并没有思考数学知识之间的内在统一性，没有厘清知识的来龙去脉，在提问题时非常随意，东一榔头西一棒。学生在教师的牵引下，进行着无序的探究与思考，他们所能获得的只是一些零散的、可怜巴巴的知识的碎片。

2.问题的浅表性

数学教学是一个由浅入深、由表及里的过程，如果数学问题始终停留在知识的表面，学生无须思考，或略加思考便可以解决，那么这样的问题是缺少思维张力的，学生的学习无法真正发生。需要指出的是，有些教师提出的问题根本与学科知识无关，譬如“是不是”“对不对”“好不好”之类的判断性、评价性问题。

3.问题的封闭性

乔森将问题分为两类：一类是良构问题；一类是劣构问题。良构问题往往有确定性条件、同一性解决方案。在课堂教学中，许多教师提出的问题都是良构性问题，属于微解答距或者短解答距类问题，学生只需查阅文本或者模仿例题即可[2]。这类问题是封闭的，学生的思维只能沿着一条直线前行，缺乏挑战性和趣味性。

二、内涵探微：究竟何为基于核心问题的小学数学对话教学

基于核心问题的小学数学对话教学，是指以核心问题为载体和依托，以和谐对话为主体样式和路径，以建构知识和生成意义为旨归的教学形态。核心问题是统领一节课的中心问题、关键性问题，核心问题可以决定对话的动机、指引对话的思路、规约对话的内容、作为对话的目的。基于核心问题的小学数学对话教学相对于一般意义上的数学对话教学又具有以下的特征：

1.师生的民主性

对话不仅仅是一种形式，更是一种精神、一种存在方式、一种哲学思维，它强调的是师生之间的平等、民主、尊重和爱，是师生之间的意义共享和精神穿越。核心问题引领下的小学数学对话教学，教师和学生都置身于现实的、富有意义的探究情境之中，师生不再是单向度的我—他关系，而是双向度的我—你关系。诚如萧伯纳所吟唱：“我是你的一个旅伴，你向我问路，我指向我俩的前方。”[3]

2.问题的统整性

核心问题是课堂的中心问题，它往往直击知识的本质，切中学习的重点和难点，扣准学生思维的困惑。核心问题中的一问抵用许多问，具有提纲挈领的功效。核心问题引领下的课堂往往呈现出一种板块式、回旋式的结构，具有大空间、大格局。例如“百分数的认识”一课，我们可以提出如下三个问题：什么是百分数？百分数与分数的关系是什么？为什么要学习百分数？这三个问题使得课堂层次分明、重点突出、结构完整。

3.学习的交互性

对话教学的一个重要特点就是交互性，而核心问题引领的对话教学则让这一特点更为凸显。一方面，核心问题基于现实的、富有挑战性的情境，学生独立的学习往往较难获得问题的解决，它需要生生之间、师生之间的交往互动、合作共享；另一方面，核心问题打开了学生的思维路径，多样的、个性化的学习方式使得每个学生都成了他人学习的资源，互学、互教成为课堂常态。这样，“你有一种思想，我有一种思想，两人交换，每人就都有了两种思想”。

4.思维的深刻性

郑毓信教授指出：我们应当通过数学教学帮助学生学会思维，并能逐步学会想得更清晰、更深入、更全面、更合理，包括由“理性思维”逐步走向“理性精神”[4]。核心问题注重了问题的数量和质量，留给了学生足够的空间和时间，学生可以从蜻蜓点水式的思考中走出来，从机械的“一问一答”中走出来，他们思维能够充分打开，能够往宽处想、往深处想、往高处想，进而不断提升他们的思维品质。如“异分母分数加减法”一课，核心问题就可以确定为：异分母分数能直接相加减吗？为什么？应该怎么做？这样的问题促使学生深刻认识：只有统一计数单位才可以相加减。

三、策略追寻：如何实施基于核心问题的小学数学对话教学

1.在知识本质处设置核心问题，让对话有深度

老子说：道生一，一生二，二生三，三生万物。所谓的道就是知识的本质，数学的本质就是去除物理属性之后抽象出的事物的数和形上的特征。知识的本质是知识之根、知识之核，它是一种具有再生长能力的知识。在数学教学中，教师必须在知识本质之处设置核心问题，引导学生探究、辩论、质疑，进而在抽丝剥笋、由浅入深的过程中完成知识的建构以及意义的生成。“认识负数”这一内容于小学生而言是一种“人为的数”，它是为了满足计算的封闭性而引发的数系的扩充。相对小学阶段其他数的学习而言，负数是比较抽象的，如何引导学生从不同的角度来认识负数，我们设置了如下的核心问题：从大小上看负数是怎样的数？从意义上看负数是怎样的数？从样子上看负数是怎样的数？这三个问题涉及负数的写法、大小以及意义，而意义极为关键，学生只有弄清负数是表示“相反意义的量”，才算真正意义上理解了负数，把握了负数的本质。再如“分数的意义”一课，我们仅仅提出了两个问题：把谁看作一个整体？是怎么分的？前者重在让学生把握无论是一个物体、一个图形、一个单位长度或者一个整体都可以看作单位“1”；后者则进一步凸显了分数既是对象又是过程的特点，让学生在动态的过程中获得对分数的真正理解。

2.在关键方法处设置核心问题，让对话有力度

经常有人说：要教给学生带得走的知识。什么是带得走的知识？在笔者看来就是数学的关键方法、数学化的思维。在数学教学中，教师要在数学的关键方法处设置核心问题，并且通过师生、生生之间的深度对话，让学生把握关键方法，实现关键方法的迁移。数学课程中涉及不同层面的数学方法，一般性的方法如发现规律中的猜想与验证，策略性的方法如解决问题中的假设与画图，特殊性的方法如计算教学中的凑十与破十。在教学中，教师要凸显方法的优越性与迁移性，要借助追问、重复、归纳使得方法不断得以内化，使得课堂对话充满力量感。如教学“和差问题”一课时，我们在学生把握了此类问题的特征后，仅提出了一个问题：怎样把两个量变得同样多？学生在自主探究、知识共享中提出了截长、补短、移多补少的方法，而这些方法的最终目的就是成功地将两个量转化成一个量，进而获得问题的解决。再如教学“圆的面积”时，教师首先让学生回顾平行四边形、三角形、梯形的面积分别是如何推导的，然后教师提出两个问题：怎样把圆转化为一个和它面积相等的已经学过的图形？这两个图形之间有什么联系？学生通过猜想、尝试、比较、归纳，再借助师生、生生之间的深度对话，成功推导出圆的面积。

3.在经验生长处设置核心问题，让对话有温度

数学学习是离不开经验的，学生的生活经验、知识经验、思维经验对于学生的学习都有着重要的影响。奥苏泊尔曾说：假如让我把全部教育心理学仅仅归纳为一条原理的话，那么，我将一言以蔽之：影响学习的唯一最重要的因素，就是学习者已经知道了什么。要探明这一点，并应据此进行教学[5]。事实上，数学教学只有基于学生的经验，在学生经验的生长处着力，学生才会具有学习的动力，才能使得新的知识不是建在沙滩上的高楼，课堂也才有温度。如“长方形的面积”一课，教师可以借助长4 cm、宽3 cm的长方形，只需提出一个问题：你能借助1 cm2的小正方形卡片摆一摆，算出长方形的面积吗？这样的问题是开放的，可以面向不同思维水平的学生。有的学生用12个1 cm2的正方形摆满了长方形，有的学生仅仅摆了一行一列，还有的学生没有摆而是用铅笔分成了相应的段数……这样的过程充分尊重学生已有的经验，让新知在探究中自然生长，不同的思维方法让对话充满了温度。又如“认识厘米”一课，最最重要的就是帮助学生建立起1 cm有多长的表象，我们设置了三个问题：你能在直尺上找到1 cm吗？生活中还有哪些物体的长度也是1 cm？凭感觉你能创造出1 cm出来吗？这一过程让学生经历了一个由外向内、由内向外的思维过程，这一过程中学生相互补充、相互验证，有效激活了学生的思维，丰富了学生的经验。

4.在思想渗透处提出核心问题，让对话有高度

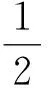
诚然，数学课堂永远是一个开放的、变动的、多彩的世界。数学课堂教学不同的内容也应该有着不同的思路，相同的思路也有着不同的课堂姿态。需要指出的是，基于核心问题的小学数学对话教学只是众多课堂样式中的一种，我们没有必要也不可能用一种模式去统领所有的课堂。更重要的是，我们要领略问题的实质，把握对话的精神，不断更新自己的教学理念，逐步改变自己的教学行动，让儿童的思维素养真正得到提升。

[1]袁庆晖.“基于问题的对话教学模式”初论[J].中小学教师培训，2005(11)：38.

[2] 宗彪.基于高级思维能力发展的深度对话教学[J].中小学管理，2014(12)：106.

[3] 冯茁.教育场域中的对话[M].北京：教育科学出版社，2010：60.

[4] 郑毓信.为学生思维发展而教[J].小学教学(数学版)，2017(5)：5.

[5] 曹才翰，章建跃.数学教育心理学[M].北京：北京师范大学出版社，2006：56.

[6] 王玉东.感悟思想：数学教学的理性追求[J].小学数学教与学，2013(3)：7.