赣南凝灰岩残积土水-力相互作用特性研究

谭宏大,简文星,卢 游,宋 治

(中国地质大学(武汉)工程学院，湖北 武汉 430074)

我国南方火成岩分布广泛且风化作用强烈，形成大量残积土土质斜坡，在降雨等因素作用下易产生斜坡的变形破坏。目前研究人员对花岗岩残积土的研究较多[1-6]，对其他类型的残积土的研究相对较少。凝灰岩残积土在我国东南沿海地区分布较为广泛，对其工程特性进行研究显得十分必要。目前已有许多学者对凝灰岩残积土的有关工程特性进行了研究，如丁少林等[7]通过试验探讨了凝灰岩残积土基质吸力随含水率的变化规律；Zuo等[8]通过研究发现含水率和干湿循环对凝灰岩残积土的结构具有显著的影响；Wang等[9]研究了凝灰岩残积土与花岗岩残积土在剪切条件下的差异。

土的水-力相互作用特性的研究包括土-水特征曲线、渗透系数函数、吸应力和非饱和抗剪强度等方面。胡孝彭等[10]讨论了不同应力状态对土-水特征曲线的影响规律；陈辉等[11]建立了一种确定非饱和土的土-水特征曲线的方法；祝艳波等[12]通过试验研究了巴东组非饱和红土的基质吸力特征，并提出了经验抗剪强度公式；刘子振[13]基于非饱和土双应力理论，提出了不同含水率条件下非饱和土的抗剪强度公式，并分析了其对边坡稳定性的影响。

赣南山区凝灰岩残积土风化层较厚，区域内降雨量较大，在高速公路建设过程中形成了大量凝灰岩残积土边坡，在降雨入渗作用下边坡土体的基质吸力、渗透系数、吸应力和抗剪强度不断发生变化，致使边坡的安全稳定性不断变动，容易导致边坡的变形破坏。本文重点研究了凝灰岩残积土水-力相互作用的特性，可为赣南山区凝灰岩残积土边坡的稳定性分析和防护设计提供参考。

1 凝灰岩残积土的物理性质和抗剪强度特性

1. 1 凝灰岩残积土的物理性质

本文通过采集江西安定高速公路A2标段YK170+460～YK170+860右侧试验边坡处典型的凝灰岩残积土原状试样，对其进行了物理性质试验，得到该凝灰岩残积土原状样的基本物理性质参数，详见表1。

表1 凝灰岩残积土原状样的基本物理性质指标

由表1可见，凝灰岩残积土原状样的孔隙率较大，渗透系数较小，渗透能力差，且塑性指数较大。

1. 2 凝灰岩残积土的抗剪强度特性

本文采用三轴固结不排水剪切试验研究了凝灰岩残积土原状样的抗剪强度特性。采用的试验仪器为南京泰克奥科技有限公司生产的TRA三轴剪切渗流仪。凝灰岩残积土原状样用切土器切削制成，试验样品规格为直径39.1 mm×高度80 mm，并采用抽真空饱和的方法使试样充分饱和。通过试验得到试样的应力-应变关系，并根据摩尔-库仑破坏准则可得到凝灰岩残积土原状样的抗剪强度参数[14]，详见表2。

表2 凝灰岩残积土原状样的抗剪强度参数

由表2可见，凝灰岩残积土原状样的总黏聚力为14.0 kPa、总内摩擦角为15.6°，有效黏聚力为7.8 kPa、有效内摩擦角为28.0°。

2 凝灰岩残积土的水-力相互作用特性

2. 1 试验方法及原理

本次试验采用美国科罗拉多矿业大学Ning Lu等联合研发的瞬态脱湿与吸湿试验系统[15]，可以得到脱湿与吸湿条件下全吸力范围内(0～106kPa)土样的土-水特征曲线、渗透系数函数曲线和吸应力曲线。试验样品为直径61.8 mm×高度40 mm的标准环刀样。试验土样先经抽真空饱和，脱湿状态下在压力室中先施加较小的空气压力使土样进行排水，待水不再排出时再施加较大的空气压力使土样继续排水直至平衡；脱湿过程结束后将气压调零，使土样进入吸湿状态直至达到重新饱和。

土样中水流出的瞬态改变量是土样特有的时间函数关系。通过试验测得土样中水的瞬态流出量可作为目标函数曲线用于反演模拟计算[16]，利用Hydrus-1D程序反演计算可得到凝灰岩残积土原状样在脱湿与吸湿过程中水-力特征曲线的模型参数。本文选取的凝灰岩残积土原状样，试样编号为NY-1、NY-2，通过试验获取其流出水量与时间的关系曲线(见图1)，通过反演计算可以得到试样NY-1、NY-2在脱湿与吸湿过程中水-力特征曲线的各模型参数，见表3。

由表3可见，脱湿过程中α(进气值的倒数)、n(与孔隙特征相关参数)均大于吸湿过程中的α、n；脱湿过程中θs(饱和体积含水率)、Kw(饱和渗透系数)均小于吸湿过程中的θs、Kw，而模型参数的不同决定了脱湿与吸湿过程中凝灰岩残积土水-力相互作用特性的差异。

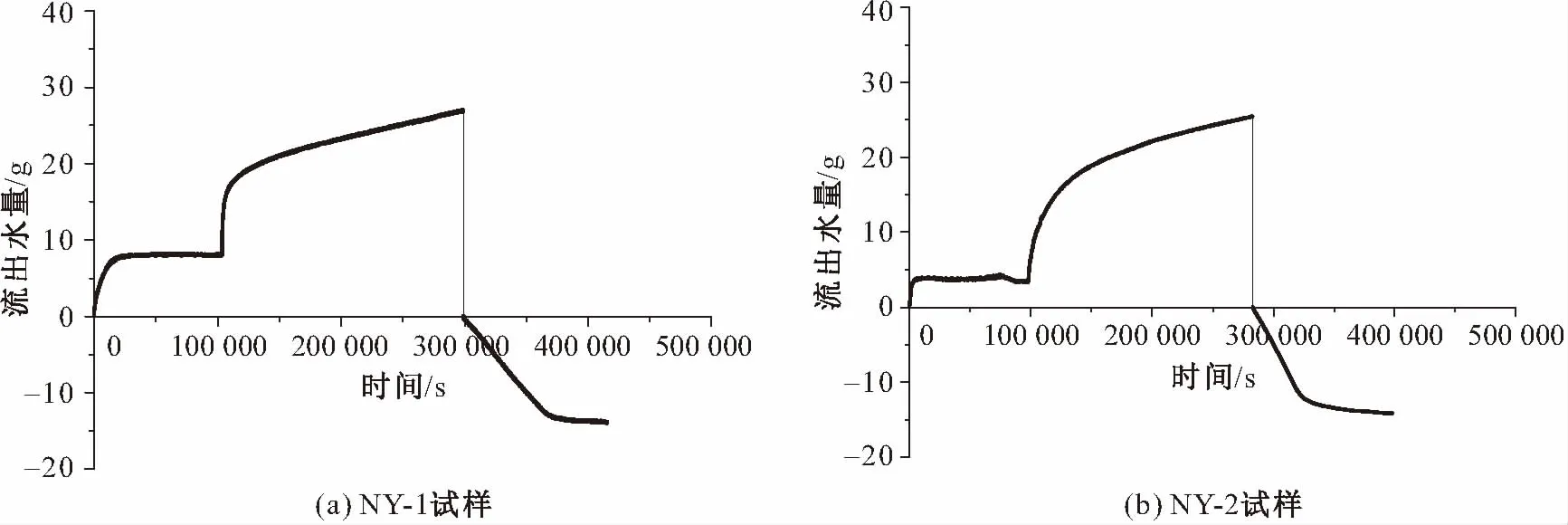
图1 凝灰岩残积土原状样中流出水量与时间的关系曲线Fig.1 Curves of outlet water of undisturbed samples of the tuff residual soil with time

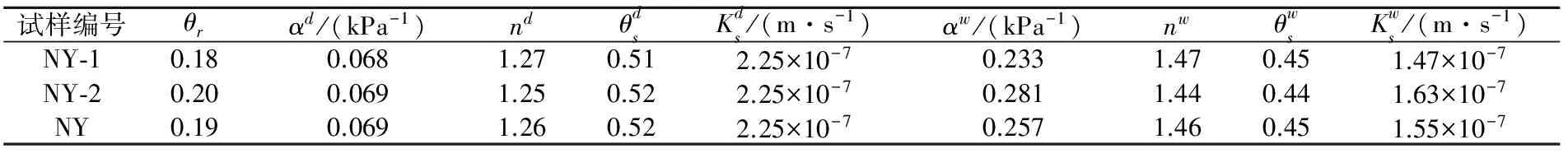
试样编号θrαd/(kPa-1)ndθdsKds/(m·s-1)αw/(kPa-1)nwθwsKws/(m·s-1)NY⁃10．180．0681．270．512．25×10-70．2331．470．451．47×10-7NY⁃20．200．0691．250．522．25×10-70．2811．440．441．63×10-7NY0．190．0691．260．522．25×10-70．2571．460．451．55×10-7

本研究选取试样NY-1、NY-2两者各模型参数的平均值作为凝灰岩残积土原状样的模型参数，试样编号为NY(见表3)，来研究其水-力相互作用的特性。

参数α为土样进气压力值的倒数，由表3可见，凝灰岩残积土典型代表试样NY在脱湿与吸湿条件下α值分别为0.069 kPa-1与0.257 kPa-1，因此可估算出凝灰岩残积土原状样在脱湿条件下的进气压力值为14.6 kPa，在吸湿条件下的进气压力值为3.89 kPa。

2.2 凝灰岩残积土的土-水特征曲线和渗透系数函数曲线

为了获得土体基质吸力随含水率变化的关系式，众多研究人员在试验的基础上，提出了多种本构关系式，如Brooks-Corey(BC)模型、Fredlund-Xing(FX)模型和Van Genuchten(VG)模型。其中，VG模型的数学表达式包含了曲线中转折点的信息，吸力范围较广，能更好地拟合实际的土-水特征曲线的形状。简化VG模型的表达式如下：

θ-θrθs-θr=11+[α|h|]n〗1-1n

(1)

式中:θ为土体任意时刻的体积含水率；θr为土体残余体积含水率；θs为土体饱和体积含水率；h为土体基质吸力水头(m)；α为拟合参数，为土体进气值的倒数(kPa-1)；n为拟合参数，与土体孔隙尺寸分布有关。

随着土体含水率的变化，土体的渗透系数也会发生变化，因此测定非饱和土体不同含水率对应的渗透系数非常困难。通过瞬态脱湿与吸湿试验，可得到用于确定非饱和土体渗透系数函数关系曲线的模型参数。本文采用Mualem模型，其表达式如下：

K=Ks{1-(α|h|)n-1[1+(α|h|)n]1n-1}2[1+(α|h|)n]12-12n

(2)

式中:K为非饱和土体的渗透系数函数(m/s)；Ks为土体的饱和渗透系数(m/s)，可通过试验测得；其余参数意义同上。

以凝灰岩残积土原状样NY为代表，根据表3中的参数，并结合式(1)和式(2)，可分别得到凝灰岩残积土的土-水特征(SWCC)曲线和渗透系数函数(HCF)曲线，见图2。

图2 凝灰岩残积土的SWCC和HCF曲线Fig.2 SWCC and HCF curves of the tuff residual soil

由图2凝灰岩残积土的土-水特征曲线(SWCC)可以看出：凝灰岩残积土在脱湿和吸湿条件下的土-水特征曲线存在明显的滞后效应。随着含水率的减小，土样的基质吸力不断增大，且其增长速率逐渐加快；从饱和含水率到残余含水率的变化范围，土样的基质吸力从0 kPa增长到106kPa；在相同含水率时，脱湿条件下土样的基质吸力大于吸湿条件下的基质吸力；基质吸力相同时，土样在脱湿过程中的含水率比吸湿过程中的含水率大；吸湿条件下土样的饱和含水率比脱湿条件下的饱和含水率低，其原因是土样经过脱湿过程后，在进行吸湿过程时试样中产生了一定量的闭合气泡，因而在吸湿过程结束后，试样无法达到完全饱和的状态。

由图2中凝灰岩残积土的渗透系数函数(HCF)曲线可以看出：凝灰岩残积土在脱湿条件下的饱和渗透系数为2.25×10-7m/s，在吸湿条件下的饱和渗透系数为1.47×10-7m/s，渗透系数随土样含水率的减小而不断减小，且在含水率较大时，土样的渗透系数减小得更快；在基质吸力相同时，脱湿条件下土样的渗透系数大于吸湿条件下的渗透系数。

由此可知：凝灰岩残积土边坡在脱湿条件下边坡土体的渗透性能不断减弱，在降雨入渗等吸湿条件下边坡土体的渗透性不断增强。

2. 3 凝灰岩残积土的吸应力

Lu等[17-18]提出用吸应力σs取代Bishop有效应力参数χ和基质吸力来定义土-水粒间力，并提出了土体吸应力与基质吸力或饱和度的函数关系式,即

σs=-Se(ua-uw)=-S-Sr1-Sr(ua-uw)

=-θ-θrθs-θr(ua-uw)

(3)

式中：σs为土体吸应力(kPa)；S为土体饱和度；Sr为土体残余饱和度；Se为土体有效饱和度；ua为土体孔隙气压力(kPa)；uw为土体孔隙水压力(kPa)；其余参数意义同上。

Lu等[15]进一步阐释了吸应力的热力学意义：吸应力是土-水粒间力储存的能量。经过公式推导，可得到以基质吸力S[S=(ua-uw)]形式表示的土体吸应力闭型方程:

σs=-S[1+(αS)n](n-1)n

(4)

式中：各参数意义同上。

根据表1中参数和式(4),可绘制凝灰岩残积土的吸应力(SSCC)曲线,见图3。

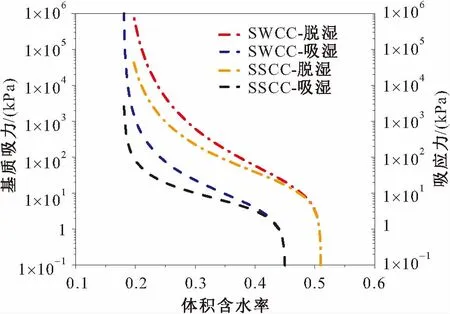
图3 凝灰岩残积土的SWCC和SSCC曲线Fig.3 SWCC and SSCC curves of the tuff residual soil

由图3可见，凝灰岩残积土的SSCC曲线与SWCC曲线呈一一对应的关系，土样的吸应力小于基质吸力，且随着含水率的减小，吸应力与基质吸力的差距不断增大，土样的吸应力随含水率的增大而减小；在含水率相同时，土样在脱湿条件下的吸应力大于在吸湿条件下的吸应力。

由此可知：凝灰岩残积土边坡在降雨入渗、毛细水上升等吸湿过程中边坡土体的吸应力不断减小，在蒸发、重力排水等脱湿过程中边坡土体的吸应力不断增大。

2. 4 凝灰岩残积土的非饱和抗剪强度

Lu等[19]提出的吸应力理论，可计算凝灰岩残积土的非饱和抗剪强度，其计算公式如下：

τf=c′+[(σ-ua)-σs]tanφ′

(5)

式中：τf为土体的抗剪强度(kPa)；c′为土体的有效黏聚力(kPa)；φ′为土体的有效内摩擦角(°)；σ为土体的轴向压力(kPa)；其余参数意义同上。

利用式(5)和表2中凝灰岩残积土的抗剪强度参数c′、φ′值，可得出凝灰岩残积土的非饱和抗剪强度计算表达式为

τf=7.8+[(σ-ua)-σs]tan28°

(6)

式中：各参数意义同上。

结合式(4)，(σ-ua)表示净法向应力，可得到凝灰岩残积土原状样(NY)在不同净法向应力条件下(100 kPa、200 kPa、300 kPa)脱湿与吸湿过程的非饱和抗剪强度曲线，见图4和图5。

图4 凝灰岩残积土在不同净法向应力条件下脱湿过程的非饱和抗剪强度曲线Fig.4 Curves of unsaturated shear strength of the tuff residual soil under drying condition and different net normal stresses

图5 凝灰岩残积土在不同净法向应力条件下吸湿过程的非饱和抗剪强度曲线Fig.5 Curves of unsaturated shear strength of the tuff residual soil under wetting condition and different net normal stresses

由图4和图5可见，凝灰岩残积土的抗剪强度随含水率的增大而减小，且土体承受净法向应力越大，其抗剪强度越大；当含水率较小时，土体抗剪强度随含水率的增大变化速率较快，当含水率较大时，土体抗剪强度随含水率的增大变化速率明显变小。

由此可知：凝灰岩残积土边坡在降雨入渗等吸湿条件下，随着含水率的增大，边坡土体抗剪强度不断减小，边坡的安全稳定性系数相应减小，导致原本处于稳定状态的边坡可能发生变形破坏。因此，在边坡的稳定性分析时必须充分考虑地下水及降雨等水的因素对边坡的影响，且在边坡的治理和防护设计中应将边坡的截排水工程作为重要的治理和防护措施。

3 结 论

本文采用三轴固结不排水剪切试验和瞬态脱湿与吸湿试验，对赣南山区凝灰岩残积土的抗剪强度和水-土相互作用特性进行了研究，得出如下结论：

(1) 凝灰岩残积土的抗剪强度参数为c=14.0 kPa、φ=15.6°，c′=7.8 kPa、φ′=28.0°。

(2) 凝灰岩残积土在脱湿和吸湿条件下土-水特征曲线存在明显的滞后效应；凝灰岩残积土在脱湿和吸湿条件下的基质吸力随含水率的增大而减小，渗透系数随含水率的增大而增大。

(3) 凝灰岩残积土在脱湿条件下的吸应力大于吸湿条件下的吸应力，且在脱湿和吸湿条件下凝灰岩残积土的吸应力随含水率的增大而减小。

(4) 凝灰岩残积土的抗剪强度随含水率的增大而减小，当含水率较大时，土体抗剪强度随含水率的增大变化速率明显变小，且在接近残余含水率时，土体的抗剪强度变化幅度较大。

[1] 吴能森.花岗岩残积土的分类研究[J].岩土力学,2006,27(12):2299-2304.

[2] Onodera T,Oda M,Minami K.Shear strength of undisturbed sample of decomposed granite soil[J].SoilsandFoundations,1976,16(1):17-26.

[3] 赵建军,王思敬,尚彦军,等.全风化花岗岩抗剪强度影响因素分析[J].岩土力学,2005,26(4):624-628.

[4] 肖晶晶.花岗岩残积土的结构性及应力应变关系试验研究[D].广州:华南理工大学,2012.

[5] 周小文,刘攀,胡黎明,等.结构性花岗岩残积土的剪切屈服特性试验研究[J].岩土力学,2015,36(S2):157-163.

[6] 许旭堂,简文彬,柳侃.含水率和干密度对残积土抗剪强度参数的影响[J].地下空间与工程学报,2015,11(2):364-369.

[7] 丁少林,左昌群,刘代国,等.非饱和残积土土-水特性研究及基质吸力估算[J].长江科学院院报,2016,33(3):98-103.

[8] Zuo C Q,Liu D G,Ding S L,et al.Micro-characteristics of strength reduction of tuff residual soil with different moisture[J].JournalofCivilEngineering,2016,20(2):639-646.

[9] Wang Y H,Yan W M.Laboratory studies of two common saprolitic soils in Hong Kong[J].JournalofGeotechnicalandGeoenvironmentalEngineering,2006,132(7):923-930.

[10]胡孝彭,赵仲辉,倪晓雯.应力状态对土-水特征曲线的影响规律[J].河海大学学报(自然科学版),2013,41(2):150-155.

[11]陈辉,韦昌富,李幻,等.测定非饱和土土-水特征曲线的溢出水校正称量法[J].岩土力学,2010,31(7):2141-2145,2152.

[12]祝艳波,余宏明,高建伟,等.巴东组非饱和红土强度与变形特性实验研究[J].工程地质学报,2012,20(6):1050-1056.

[13]刘子振.持续降雨入渗非饱和黏土边坡失稳机理及其应用研究[D].兰州:兰州大学.2014.

[14]卢游,简文星,王立宸,等.赣南凝灰岩残积土物理力学与应力-应变特性研究[J].安全与环境工程,2017,24(1):16-21.

[15]Lu N,Godt J W.斜坡水文与稳定[M].简文星，王菁莪，侯龙，译.北京:高等教育出版社,2014.

[16]Sun P P,Zhang M S,Zhu L F,et al.Discussion on assessment in the collapse of loess:A case study of the Heifangtai terrace,Gansu,China[C]//LandslideScienceforaSaferGeoenvironment,Volume2:MethodsofLandslideStudies.WorldLandslideForum3.Beijing:[s.n.],2014:195-199.

[17]Lu N,Likos W J.Rate of capillary rise in soils[J].JournalofGeotechnicalandGeoenvironmentalEngineering,2004,130(6):646-650.

[18]Lu N,Wayllace A,Carrera J,et al.Constant flow method for concurrently measuring soil-water characteristic curve and hydraulic conductivity function[J].GeotechnicalTestingJournal,2006,29(3):256-266.

[19]Lu N,Lioks W J.Suction stress characteristics curve for unsaturated soil[J].JournalofGeotechnicalandGeoenvironmentalEngineering,2006,132(2):131-142.