基于幂函数的边坡岩体泥质夹层长期强度直剪蠕变试验研究

周晓飞，孙金山，刘贵应，李正川，易 兵

(1.中国地质大学(武汉)工程学院，武汉 430074；2.中铁二院重庆勘察设计研究院有限责任公司， 重庆 400023；3.重庆城市综合交通枢纽开发投资有限公司，重庆 400023)

岩质边坡中往往存在一定数量的软弱结构面，在岩体自重和降雨、地震等外在因素的作用下边坡常沿此类软弱结构面发生滑动，进而导致滑坡灾害。软弱结构面一般都具有显著的流变性，致使受其控制的边坡也呈现出典型的流变变形和渐进失稳特征。

目前，国内外对岩体流变特性的研究已取得了一定的研究成果，但主要成果集中在岩石材料流变性质的研究方面。岩体的流变性质是岩体的重要特性之一，在力的作用下岩块和结构面均产生流变变形，岩体的长期强度一般取决于两者的流变特性，在一些情况下结构面的流变特性显得更为重要。徐卫亚等[1]对节理岩体的流变特性进行了研究，建立了节理岩体的剪切流变模型；朱珍德等[2]通过对岩石夹层剪切流变试验结果的分析，获得了岩体结构面的长期强度参数，并指出黏聚力对剪切流变的影响略高于内摩擦角；李翔等[3]借助Flac3D软件中的Burger模型对滑带土室内三轴蠕变试验进行了数值模拟，获取了滑带土长期强度参数；熊良宵等[4]采用广义Kelvin模型、Burgers模型和六元件黏弹性流变模型，提出硬性结构面的剪切流变模型及剪切蠕变试验的数值分析方法；庞正江等[5]针对某电站典型代表性的岩层进行室内岩石剪切流变试验，选取扩展的Burgers模型建立流变方程，利用MATLAB工具函数fminsearch拟合试验得到的μ-t非线性函数流变曲线，确定了岩体结构面的流变参数；李建伟等[6]在滑坡滑带土蠕变试验的基础上，建立了反映滑带土蠕变特性的Singh-Mitchell蠕变模型；赵宝云等[7]深入研究了重庆市某干线公路顺层滑坡的垮塌机理，指出结构面流变是该滑坡发生的主要原因，并提出了适用于分析软弱结构面的顺层滑坡稳定性问题的非线性黏弹塑性流变模型;朱赛楠[8]认为滑坡蠕滑变形失稳的关键因素是软弱夹层和岩溶带的强度衰减，提出了鸡尾山型滑带软弱夹层的三个演化阶段，揭示了受软弱夹层控制的层状基岩滑坡的失稳机理；简文星等[9]从红层岩土体蠕变特性研究入手，探讨了在降雨作用下缓倾角红层基岩滑坡的启滑机制；陈沅江等[10]着重研究了结构面粗糙突起阻滞作用和摩擦阻滞作用对结构面蠕变过程的影响；曹运江等[11]针对坝区开挖高边坡煤系地层软弱结构面开展了软弱结构面的时效变形特性研究，建立了各种类型软弱结构面的综合时效本构方程，获取了坝区煤系地层软弱结构面的长期强度参数。但是，由于结构面的流变性质非常复杂，影响因素也很多，相关的研究成果还比较少，如今岩体滑坡、围岩塌陷屡见不鲜，这些频发的工程事故大多与岩体结构面的流变特性有关，因此开展对岩体结构面剪切流变特性的试验研究，对于整个岩体工程的长期稳定性具有重要的指导价值，而且能为岩体流变特性理论研究提供必要的基础。为此，本文主要针对边坡岩体中的泥质夹层，通过泥质夹层的室内直剪蠕变试验，在试验的基础上，采用幂函数描述泥质夹层蠕变变形随时间的变化情况，并确定了泥质夹层的长期强度。

1 泥质夹层剪切蠕变特征

通常泥质夹层的抗剪强度是由室内试验将夹层试样在规定时间内破坏测得，然而，现实中的岩体沿泥质夹层剪切破坏一般都是在很长一段时间之后发生的。泥质夹层的长期强度是指夹层在强度范围内能够长期稳定存在的界限值。岩体的泥质夹层具有遇水软化和变形随时间变化的特性，特别是对于含有大量黏土矿物的泥质夹层，其蠕变变形更为明显。图1为泥质夹层的剪切蠕变曲线。

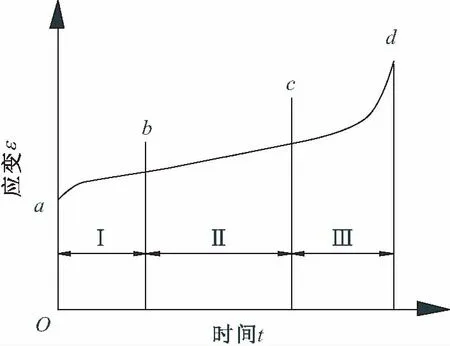
图1 泥质夹层剪切蠕变曲线[12]Fig.1 Shear creep curve of the mudded intercalation[12]

由图1可以明显地看出泥质夹层剪切蠕变的三个阶段，即蠕变初始阶段I(图1中ab段)、蠕变稳定阶段II(图1中bc段)、蠕变加速阶段III(图1中cd段)。

对应于泥质夹层的蠕变变形阶段，泥质夹层长期强度值即为夹层不发生蠕变加速阶段的界限值。为了确定泥质夹层的长期强度，本文拟通过对泥质夹层进行直剪蠕变试验，通过分析其蠕变变形特性，进而获得其长期强度。

2 泥质夹层的直剪蠕变试验

2. 1 剪切蠕变加载方式

目前比较流行的蠕变加载方式有分样加载和分级加载，两种加载方式有各自的优缺点。

分样加载，即对试样一次性加到某个蠕变荷载，然后维持恒定。优点：没有前期应力历史的影响；缺点：需一组同样的试样，难以避免结果离散性。

分级加载，即对一个试样进行多级加载。优点：只需进行一个试验；缺点：上一级荷载对下一级荷载变形有影响。本次试验拟采用分级加载的方式。

2. 2 试验仪器

边坡岩体泥质夹层一般都处于一定的应力水平下，为了使试验更接近实际泥质夹层的状态，本次试验使用南京仪器厂生产的ZLB-三联直剪流变仪。该仪器能够实现在土样上施加一定法向压力，同时在剪切面上施加一定的剪切力，并对土样的剪切变形量进行测试。该仪器的试样尺寸为φ61.8 mm×20 mm，最大剪切力为1.8 kN，最大法向力为1.8 kN。

2. 3 试样制备

试样取自岩质边坡红黏土泥质夹层，其基本参数见表1。

表1 试样基本参数

为了使得泥质夹层流变变形更为明显，本次试验采用饱和土体，并考虑到泥质夹层一般都处于一定的应力水平下，试样采用以下方法制作：待土体饱和后，将饱和土体制作成直径为61.8 mm、厚为20 mm的标准剪切试样，并在150 kPa的法向荷载下固结24 h。

2. 4 试验内容

本次试验共分为2组，试验方案如下：

(1) 将标准剪切试样分别在100 kPa、150 kPa、200 kPa的法向应力作用下进行应变式快剪直剪试验，测得试样在饱和固结之后的抗剪强度。

(2) 将标准剪切试样在150 kPa的法向应力作用下，采用分级加载方式对试样进行剪切蠕变试验，每级荷载的大小约为其抗剪强度的10%、20%、30%、40%、50%、60%、70%、80%、90%。每隔一定的时间记录剪切变形量，待试样进入稳定阶段，卸载记录回弹变形量。

2. 5 试验结果

2.5.1 直剪试验

通过直剪试验，获取了标准剪切试样的抗剪强度参数，即黏聚力c为14.19 kPa、内摩擦角φ为8.3°。标准剪切试样在150 kPa法向应力作用下的抗剪强度为36.2 kPa，为接下来的分级加载荷载值提供了参考。

2.5.2 分级加载剪切蠕变试验

试样分级加载剪切蠕变变形的试验结果，见图3。对于土体分级加载蠕变变形数据的处理主要有两种方法，分别是线性法和陈氏法，目前普遍采用陈氏法。“陈氏”处理方法的优点在于采用作图法可求得岩体真实蠕变变形过程的叠加关系，并能考虑土体的非线性蠕变变形特性。

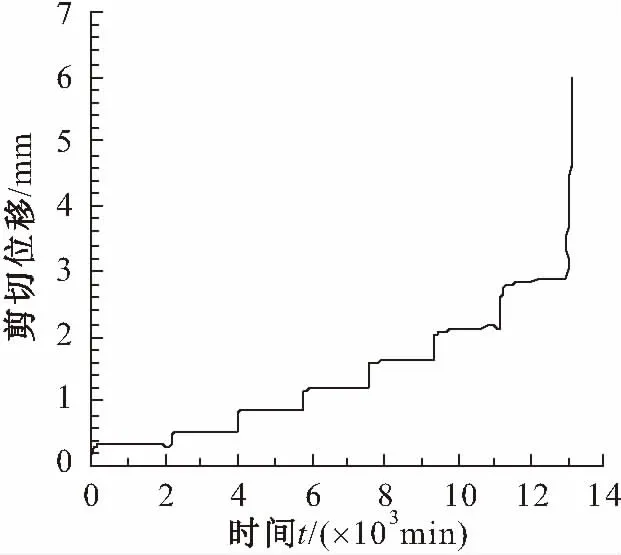
图2 试样分级加载剪切蠕变变形(σ=150 kPa)Fig.2 Creep deformation under step loading (σ=150 kPa)

本文利用陈氏法对试样分级加载蠕变变形数据进行了处理，其处理结果见图3。

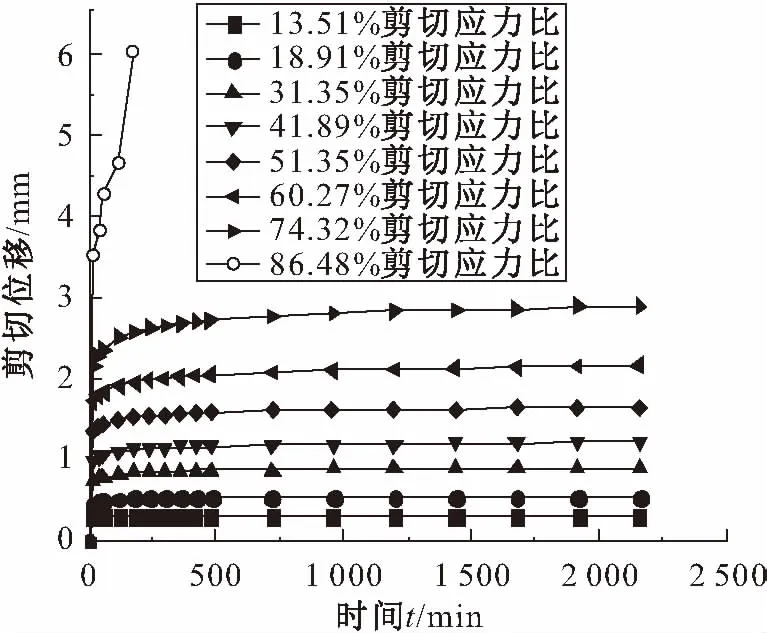
图3 试样分级加载剪切蠕变变形的叠加(σ=150 kPa) Fig.3 Superposition of creep deformation under step loading (σ=150 kPa)

3 泥质夹层长期强度的确定

3. 1 剪切变形特征

试样的剪切变形包括瞬时的弹性变形和与时间相关的蠕变变形，因此本文分开考虑其弹性变形和蠕变变形。不同剪切应力比情况下，试样达到稳定阶段的弹性变形量和塑性变形量见表2、图4和图5。

由图4和图5可以看出：试样的弹性变形量基本上与剪切应力比呈线性关系,对于给定的剪切应力比，其弹性变形为定值；而对于蠕变变形产生的塑性变形量，随着剪切应力比的增大而呈现指数增长，可见随着剪切应力比的增加，蠕变剪切位移量更大，蠕变变形也更为明显。

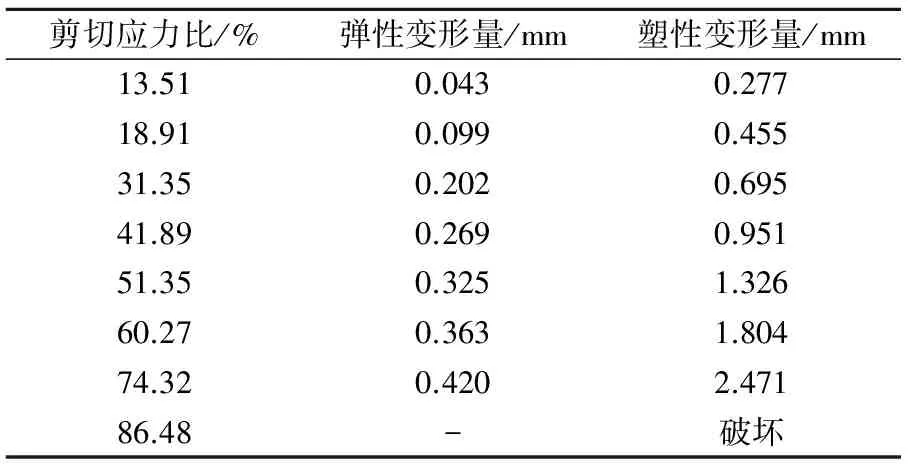
表2 不同剪切应力比下试样的弹塑性变形

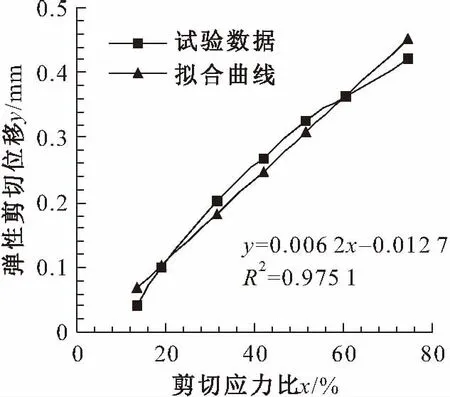
图4 不同剪切应力比下试样的弹性变形Fig.4 Elastic shear deformation under different shear stress ratios

图5 不同剪应力比下试样的蠕变变形Fig.5 Creep shear deformation under different shear stress ratios

3. 2 蠕变变形-时间函数的确定

土体蠕变变形的复杂性主要是由于蠕变变形的时间相关性。一些学者通过现象学的研究建议采用大量的函数来描述土体蠕变变形速率曲线的函数关系，其中最普遍、最适用的就是幂函数，如下式：

ΔL(t)Δt=Τ2Τ1+tp

(1)

式中:ΔL(t)为在Δt时间内土体的蠕变变形量(mm)；T1和T2为常数项；t为加载时间(min)；p为幂函数的幂级次。

通过对公式(1)进行分析可知，对于不同范围的幂级次p值，该函数呈现不同的形态，分别对应土体不同的蠕变状态。通过对公式(1)进行时间积分，可得到土体蠕变剪切位移与时间的函数，见表3。

表3 土体蠕变剪切位移与时间的函数

令公式(1)中T1=1，可得到土体蠕变剪切位移-时间函数的拟合式为

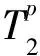
(2)

式中:L(t)为t时刻土体的蠕变变形量(mm)。

不同p值对应的土体蠕变剪切位移-时间曲线见图6。

图6 不同p值对应的土体蠕变剪切位移-时间曲线Fig.6 Curve of creep displacement-time under different p values

由图6可见，当p>1时，对应于曲线a，土体蠕变剪切位移最终趋于定值；当0

由于幂级次p值与不同应力水平下土体的蠕变剪切位移-时间曲线具有良好的对应性，且p=1对应于土体蠕变剪切位移收敛与否的分界值，因此考虑到利用幂级次p值确定土体的长期强度。

3. 3 蠕变变形的拟合

将不同剪切应力比下试样的剪切变形量减去其初始弹性变形量，即为试样的蠕变变形量。不同剪切应力比作用下试样蠕变剪切位移随时间的变化曲线，见图7。

图7 不同剪切应力比下试样的蠕变剪切位移-时间曲线Fig.7 Curve of creep displacement-time under different shear ratios

由图7可见，在13.51%的剪切应力比作用下试样基本没有蠕变变形，较快地进入蠕变稳定阶段；但随着剪切应力比的增大，试样的蠕变变形越来越明显，其蠕变进入稳定阶段的时间也较长。

本文采用公式(2)对图7中不同剪切应力比下试样的蠕变变形-时间曲线进行了拟合，其拟合曲线见图8。其中，在86.48%的剪切应力比作用下，加载120 min后试样出现了加速蠕变阶段，并在短时间内发生了剪切破坏，其拟合曲线见图9。

图8 不同剪切应力比下试样的蠕变变形拟合曲线Fig.8 Fitting curve of creep deformation under different shear ratios

图9 在86.48%的剪切应力比下试样的蠕变变形拟合曲线Fig.9 Fitting curve of creep deformation under shear stress ratio of 86.48%

由图8和图9可见，借助幂函数能够实现对试样蠕变变形的拟合。

3. 4 泥质夹层的长期强度确定

3.4.1 幂级次法

不同剪切应力比作用下试样的蠕变剪切位移-时间曲线的拟合参数，见表4。

表4 不同剪切应力比下试样的蠕变剪切位移-时间曲线的拟合参数

根据表4中数据，绘制p值随剪切应力比的变化曲线，见图10。

图10 不同剪切应力比的幂级次p值Fig.10 p value under different shear stress ratios

由图10可见，幂级次p值大小与剪切应力比呈负相关关系，并将p=1作为蠕变剪切位移-时间函数是否收敛的分界值，即p=1对应的试样剪切应力值就为其长期强度。通过作图法,求得p=1对应的剪切应力比为82% ，因此试样的长期强度为其抗剪强度的82%。

3.4.2 等时曲线法

目前确定岩体长期强度方法采用最多的是等时曲线法，根据泥质夹层试样直剪蠕变试验数据绘制其剪切变形等时曲线，见图11。

图11 试样的剪切变形等时曲线Fig.11 Isochronous curves of shear deformation

根据图11试样的剪切变形等时曲线的最大曲率，可求得泥质夹层土体的长期强度为26.8 kPa，为实际抗剪强度的74%。

可见，使用不同方法求取边坡岩体中泥质夹层的长期强度具有一定的差别，幂级次判别法将p=1作为判别标准更为严格，对应于绝对临界失稳状态，因此获取的泥质夹层长期强度较传统等时曲线法获取的长期强度要大一些。另外，边坡岩体中泥质夹层的蠕变变形容易受到人为和自然因素的影响，实际工程中还需要根据实际情况慎重进行岩土体结构面的稳定性评价。

4 结 论

确定边坡岩体结构面长期强度对于边坡等工程的长期稳定性评价具有重要的意义。本文通过对边坡岩体泥质夹层的室内直剪蠕变试验研究，提出了借助幂函数确定泥质夹层长期强度的方法，并与传统等时曲线法进行了对比，得出结论如下：

(1) 不同剪切应力比下，泥质夹层的蠕变变形特征不同，在低剪切应力比下，泥质夹层的蠕变变形不明显，且剪切应力比越大，泥质夹层蠕变变形越明显。

(2) 借助幂函数对泥质夹层蠕变剪切位移-时间曲线进行了拟合，确定了泥质夹层在150 kPa法向应力作用下的长期强度为其抗剪强度的82%，相较于传统等时间曲线法获取的长期强度要大一些。

[1] 徐卫亚,杨圣奇.节理岩石剪切流变特性试验与模型研究[J].岩石力学与工程学报,2005,24(S2):264-270.

[2] 朱珍德,李志敬,朱明礼,等.岩体结构面剪切流变试验及模型参数反演分析[J].岩土力学,2009,30(1):99-104.

[3] 李翔,程聪.基于数值模拟的滑带土蠕变特性研究[J].安全与环境工程,2014,21(4):25-29.

[4] 熊良宵,虞利军,杨昌斌.硬性结构面的剪切流变模型及试验数值分析[J].岩石力学与工程学报,2015,34(S1):2894-2899.

[5] 庞正江,胡建敏.结构面剪切流变及其长期强度试验研究[J].岩土力学,2006,27(S2)：1179-1182.

[6] 李建伟,简文星,张宏家,等.川东天台乡滑坡滑带土蠕变特征[J].安全与环境工程,2010,17(4):105-110.

[7] 赵宝云,陈志平,董倩,等.基于结构面流变特性的重庆市某干线公路顺层滑坡数值模拟研究[J].重庆建筑,2012,11(9):64-65.

[8] 朱赛楠.厚层基岩滑坡软弱夹层演化过程及控滑机理研究[D].西安：长安大学,2016.

[9] 简文星,王志俭,殷坤龙，等.三峡库区万州缓倾角红层基岩滑坡启滑机制[C]//夏才初.和谐地球上的水工岩石力学——第三届全国水工岩石力学学术会议论文集.上海：同济大学，2010:365-370.

[10]陈沅江,吴超,潘长良.一种软岩结构面流变的新力学模型[J].采矿与安全工程学报,2005,22(3):43-45.

[11]曹运江,黄润秋,唐辉明,等.某水电站高边坡煤系软弱结构面流变特性试验研究[J].岩石力学与工程学报,2008,27(S2):3732-3739.

[12]刘佑荣,唐辉明.岩体力学[M].北京：化学工业出版社,2009.