近场动力学方法在边坡稳定性分析中的应用
廖 洋,刘立胜,2,刘齐文,赖 欣,池晴佳,邵爱军
(1.武汉理工大学力学系,湖北 武汉 430070;2.武汉理工大学材料复合新技术国家重点实验室,湖北 武汉 430070;3.湖北省江汉运河航道管理处,湖北 武汉 430032)
边坡的稳定性分析在边坡防护以及施工安全等方面具有重要的意义[1-2]。传统的边坡稳定性分析一般采用极限平衡法[3-5]和有限元强度折减法[6-8]。极限平衡法在工程中有着广泛的应用,但是由于其引入了条间力关系假设来消除边坡稳定问题的静不定性,故只能得到特定条件下单一的边坡安全系数。一般情况下,极限平衡法得到的既不是上限解也不是下限解。不同于极限平衡法仅对边坡的宏观安全特性进行描述,有限元方法通过借助强度折减技术,不仅能得到边坡土体的应力及变形分布规律,还可以得到边坡的安全系数,以及边坡失稳时的塑性屈服面,即边坡滑移面。有限元强度折减法在计算边坡稳定性问题时考虑了边坡土体的非线性本构关系、复杂的载荷,甚至整个施工过程,能够较为真实地反映边坡土体的应力、变形随时间的变化情况。
近场动力学方法是Silling等[9-10]提出的一种基于非局域平均思想的一类微分-积分方法,其在处理裂纹、滑移等不连续问题方面具有较好的适应性。起初的近场动力学方法是一种基于键的非局域方法,比较简单,只能模拟简单的本构关系;其后提出的基于非常规态的近场动力学方法通过引入矩量法[11],可以得到质点的任意时刻的变形梯度以及应变。基于非常规态的近场动力学方法[12-15]作为一种非局域的无网格粒子类方法,不仅具备有限元方法的优点,而且在计算非线性问题时还具有更好的收敛性以及对不连续问题的适用性。当边坡处于临界失稳状态发生滑移时,有限元方法的计算容易出现不收敛现象,而近场动力学方法不仅能计算得到边坡达到临界状态的收敛解,还能模拟边坡的滑移过程。此外,基于非常规态的近场动力学方法可以用来实现土体的非线性本构模型,如Drucker-Prager屈服模型、摩尔-库仑屈服模型等。本课题组在土体的爆炸[16]以及边坡稳定性分析[17]方面已做了一些探索性的工作。在此基础上,本文基于摩尔-库仑屈服准则以及非关联流动法则,利用近场动力学强度折减法对引江济汉工程中出口船闸的基坑边坡的稳定性进行了分析。
1 近场动力学强度折减法
1. 1 基于非常规态的近场动力学方法
在基于非常规态的近场动力学方法中,某一质点的变形状态与其自身和邻域内其他质点的位移差有关。任意质点i与其邻域内质点j之间的相互作用力被称作力态,分别为T和T′。

图1 基于非常规态的近场动力学方法中质点及其邻域Fig.1 Particle in non-ordinary state-based peridynamics and its neighbourhood
任意质点i的变形梯度张量F,可由下式计算:

(1)

(2)
式中:Y为质点i与j之间的变形后的相对位置矢量;X为质点i与j之间的初始相对位置矢量;V′为质点j的体积;K为质点i的形状张量;w(|X|)为质点j的影响函数;H为质点i的邻域范围。
根据连续介质力学理论,物质体在时间步n+1的形态Yn+1可由前一时间步n的形态Yn计算得到:
Yn+1=Yn+Δu
(3)
式中:Δu为当前时间步n的位移增量。
因此,从时间步n到n+1的变形梯度增量G的计算公式为
G=F··F-1
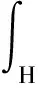
(4)
式中:F·为变形梯度F的时间导数,即速度梯度。
物质体的运动可以分为应变增量和刚体转动增量两部分:
γ=(G+GT)/2
ω=(G-GT)/2
(5)
式中:γ为应变增量;ω为刚体转动增量。
因此,有效应力增量Δσ可通过弹性矩阵De与应变增量γ进行缩并计算得到:
Δσ=De∶γ
(6)
根据Hughes-Winget理论[18],质点当前时刻n+1的柯西应力张量,可由下式计算:
σn+1=σ∧n+Δσ
(7)
σ∧n=RT·σn·R
(8)
其中,σn为时刻n的应力状态;σ∧n为σn从时刻n到时刻n+1发生刚体转动的结果;R为转动张量,可以由下式计算:
R=I+(I-0.5ω)-1·ω
(9)
式中:I为二阶单位张量。
根据柯西应力张量σn+1,可计算求得第一类皮奥拉-基尔霍夫非对称应力张量Pn+1:
Pn+1=Jσn+1F-T
(10)
式中:J为变形梯度F的行列式。
力态T和T′的计算形式如下:

(11)
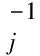
(12)
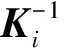
基于非常规态的近场动力学运动平衡方程为

(13)
式中:ü为质点i在t时刻的位移二阶导数,即加速度;x为质点i的初始坐标;ρ为质点的材料密度;b为质点i在t时刻受到的外力矢量作用。
根据基于非常规态的近场动力学运动平衡方程,可计算得到质点i当前时刻n的加速度,最后使用欧拉法、蛙跳法或Velocity-Verlet积分法,可求得下一时刻的质点位移,从而完成变形体的状态更新。
1. 2 强度折减法
强度折减法的基本原理是通过不断减小材料的强度参数直到边坡开始出现失稳。边坡失稳临界状态所对应的折减系数即是该边坡的安全系数,则有
ct=cini/FOS
(14)
tanφt=tanφini/FOS
(15)
式中:FOS为折减系数;ct和φt分别为边坡临界状态的内聚力和内摩擦角;cini和φini分别为边坡初始状态的内聚力和内摩擦角。
在有限元强度折减法中,当材料强度进行折减后,若有限元计算收敛,则认为边坡是稳定的;当材料强度折减到一定范围时,有限元计算开始出现不收敛的现象,此时的折减系数一般视作边坡的安全系数。
在近场动力学中引入强度折减法,其基本的计算思想与有限元法相同;不同之处是,近场动力学方法是以边坡系统的最大位移作为判断依据,当边坡处于稳定状态时,不同折减系数下边坡的最大位移值基本不变,一旦边坡失稳,边坡的最大位移值会发生较大的变化。因此,通过观察边坡最大位移值的变化,可以在近场动力学强度折减法中捕捉到边坡的安全系数。
2 摩尔-库仑屈服准则与非关联流动法则
2. 1 摩尔-库仑屈服准则
摩尔-库仑屈服准则常被用作混凝土以及岩土类材料的塑性判据。对于平面应变问题[19],摩尔-库仑准则可表示为
F=-[2ccosφ-(σx+σy)sinφ]2+(σx-σy)2+(2τxy)2=0
(16)
式中:c和φ分别为土体的内聚力和内摩擦角,σx、σy和τxy为应力分量。
对摩尔-库仑屈服准则进行线性化处理[20],令X=σx-σy,Y=2τxy,R=2ccosφ-(σx+σy)cosφ,在XOY坐标系中,屈服函数可表示成一个圆,可以使用外接多边形进行逼近。当多边形边数为p时,线性化后的屈服函数为
F=Mkσx+Nkσy+Pkτxy-2ccosφ
(17)
其中:
Mk=cosαk+sinφ
Nk=sinφ-cosαk
Pk=2sinαk
αk=2πk/p(k=1,2,…,p)
(18)
2. 2 基于非关联流动法则的弹塑性矩阵


(19)
式中:dλ为塑性应变增量的大小,它是一个非负的标量;Q为塑性势函数;σij为应力张量。
在非关联流动法则中,塑性势函数Q与屈服函数F不相等,即Q≠F。对于理想的弹塑性材料,硬化参数A为零,则应力-应变增量表达式为

(20)
式中:dεij为总的应变增量;Dep为弹塑性矩阵;De、Dp为塑性矩阵,其形式[21]如下:
Dp=∂F∂σTDe·De∂Q∂σ∂F∂σTDe∂Q∂σ
(21)
2. 3 基于摩尔-库仑屈服准则的应力更新
若屈服函数F<0,则材料处于弹性阶段,只需根据近场动力学的一般计算流程更新应力即可;若屈服函数F≥0,则材料发生了塑性变形,此时首先需要根据公式(20)和(21)计算出当前的弹塑性矩阵Dep,用以代替公式(6)中的弹性矩阵De,其应力增量为
Δσ=Dep∶γ
(22)
3 工程实例应用与分析
本文以引江济汉工程边坡为例,基于摩尔-库仑屈服准则以及非关联流动法则,利用近场动力学强度折减法对引江济汉工程中出口船闸的基坑边坡稳定性进行了分析。引江济汉工程出口船闸位于潜江市高石碑镇,闸址区地形平坦,地面高程为32.5 m。
3. 1 地层结构分布
该地区的地层结构分布如下:①亚砂土,结构松散—较密实,不均质,砂感明显,黏性差,厚度为0~2.1 m,底板高程为29.8~31.0 m;②亚黏土,可塑—软塑,黏性较强,厚度为0~2.7 m,底板高程为26.06~27.63 m;③黏土,可塑为主,局部硬塑,土质均一细腻,黏性强,厚度为6.2~16.2 m,底板高程为8.6~11.5 m;④粉细砂,饱和,稍密—中密,厚度为2.6~11.5 m。
3. 2 边坡土质及计算模型
基坑边坡地层上部为亚黏土、亚砂土、黏土,局部为淤泥质土,中下部为细砂,边坡土体较软弱。闸址地面的高程为32.5 m,最大开挖深度约17 m,边坡比取值范围为1∶2~1∶2.5。边坡土质分层情况以及边坡尺寸见图2,边坡土体近场动力学计算模型见图3,边坡土体的材料参数见表1。

图2 边坡土质分层情况以及边坡比为1∶2时的尺寸图Fig.2 Soil layers and size of the slope when the slope ratio is 1∶2

图3 边坡土体的近场动力学计算模型图Fig.3 Peridynamic model of the slope

材料土体密度/(kg·m-3)压缩模量/(MPa)泊松比内摩擦角/(°)内聚力/(kPa)亚砂土19407.40.32206亚黏土18904.40.401515黏土18404.00.421316粉细砂16908.00.29261
3. 3 计算结果与分析
保持基坑的开挖深度不变,为17.0 m,将边坡比分为1∶2和1∶2.5两种工况,使用强度折减法针对不同的折减系数FOS(1.00、1.15、1.25、1.35、1.50)分别计算得到了边坡的最大位移以及边坡的塑性应变分布情况,见图4、图5和图6。

图4 不同折减系数对应的边坡最大位移曲线Fig.4 Maximum displacements of the slope corresponding to different reduction factors
由图4(a)可见,对于边坡比为1∶2的边坡土体,当折减系数(FOS)为1.15时,边坡最大位移曲线就已经出现了不收敛,因此可以认为此时边坡的安全系数小于1.15。由图4(b)可见,对于边坡比为1∶2.5的边坡土体,当折减系数为1.15时,边坡最大位移曲线仍然是收敛的,但当折减系数为1.25时,边坡最大位移曲线出现了不收敛,因此可以认为此时边坡的安全系数小于1.25。
从以上计算结果来看,边坡的安全系数较低,边坡土体极容易发生失稳,因此可以进一步分析边坡的塑性屈服区域以及最大水平位移出现的区域。

图5 边坡比为1∶2、t=4.5 s时边坡的塑性屈服区域 分布图Fig.5 Plastic yield region of the slope when the slope ratio is 1∶2.5 and t=4.5 s

图6 边坡比为1∶2.5、t=4.5 s时边坡的塑性屈服区域 分布图Fig.6 Plastic yield region of the slope when the slope ratio is 1∶2.5 and t=4.5 s
由图5可见,当折减系数为1.00时,边坡坡脚就开始出现了塑性屈服区域,且随着折减系数的增加,坡脚的塑性屈服区域急剧增大,同时边坡上部也开始出现塑性屈服区域。对比图5和图6可见,随着边坡比的增大,边坡坡脚的塑性屈服区域明显减小,但是边坡的稳定性仍然较差,此时应加强坡脚的防护,这一结论与实际施工的情况是符合的。
当边坡比为1∶2或1∶2.5时,对于不同的折减系数,边坡的水平位移分布趋势基本相同,图7给出了边坡比为1∶2、折减系数为1.0时边坡的水平位移分布图,图8给出了不同边坡比情况下边坡最大水平位移随折减系数的变化曲线。
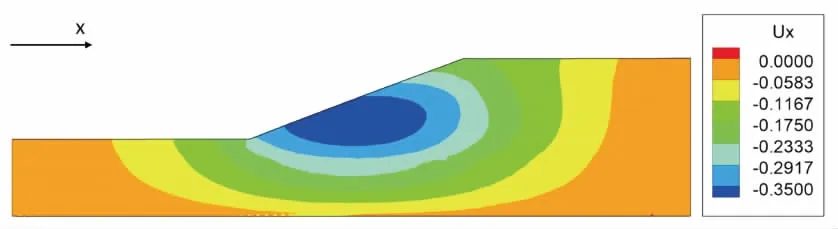
图7 边坡比为1∶2、FOS=1.0时边坡的水平位移 分布图Fig.7 Horizontal displacement when the slope ratio is 1∶2 and FOS=1.0
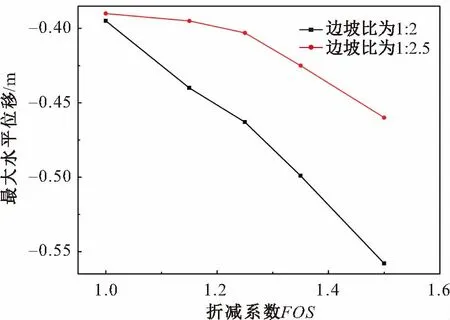
图8 不同边坡比情况下边坡最大水平位移随折减 系数的变化曲线Fig.8 Maximum horizontal displacement of the slope with the reduction factor under different slope ratios
由图7和图8可见,边坡的最大水平位移出现在坡脚的上端,且随着边坡比的增大,边坡的最大水平位移明显减小,边坡趋于稳定。
4 结 论
通过上述工程实例计算与应用,可得到如下结论:
(1) 本文所提出的基于摩尔-库仑屈服准则的近场动力学方法可以用于描述边坡土体材料的力学行为。
(2) 基于非常规态的近场动力学强度折减法可以用于边坡的稳定性分析,所得到的计算结果与实际施工情况是一致的。
[1] 杨茜,陈胜,朱桂春.基于拉格朗日乘数法的边坡稳定性变分法[J].安全与环境工程,2010,17(4):111-113.
[2] 郭利娜,胡斌,胡启晨.基于Geo Slope软件对青莲寺边坡的稳定性分析[J].安全与环境工程,2011,18(6):20-24.
[3] 朱大勇,卢坤林,台佳佳,等.基于数值应力场的极限平衡法及其工程应用[J].岩石力学与工程学报,2009,28(10):1969-1975.
[4] 孙聪,李春光,郑宏.基于整体稳定性分析法的边坡临界滑动面搜索[J].岩土力学,2013,34(9):2583-2588.
[5] 栾茂田,金崇磐,林皋.土体稳定分析极限平衡法改进及其应用[J].岩土工程学报,1992,14(S1):20-29.
[6] 张坤勇,李广山,李旺林,等.南水北调南干渠边坡有限元稳定性分析[J].河北工程大学学报(自然科学版),2016,33(4):27-32.
[7] 赵尚毅,郑颖人,时卫民,等.用有限元强度折减法求边坡稳定安全系数[J].岩土工程学报,2002,24(3):343-346.
[8] 李垠,苏凯,李杰.Mohr-Coulomb等面积圆屈服准则在边坡稳定分析中的应用[J].大地测量与地球动力学,2009,29(1):135-139.
[9] Silling S A.Reformulation of elasticity theory for discontinuities and long-range forces[J].JournaloftheMechanics&PhysicsofSolids,2000,48(1):175-209.
[10]Silling S A,Epton M,Weckner O,et al.Peridynamic states and constitutive modeling[J].JournalofElasticity,2007,88(2):151-184.
[11]Li S,Qian D,Liu W K,et al.A meshfree contact-detection algorithm[J].ComputerMethodsinAppliedMechanics&Engineering,2001,190(24/25):3271-3292.
[12]Zhou X,Wang Y,Xu X.Numerical simulation of initiation,propagation and coalescence of cracks using the non-ordinary state-based peridynamics[J].InternationalJournalofFracture,2016,201(2):213-234.
[13]Kilic B,Agwai A,Madenci E.Peridynamic theory for progressive damage prediction in center-cracked composite laminates[J].CompositeStructures,2009,90(2):141-151.
[14]Amani J,Oterkus E,Areias P,et al.A non-ordinary state-based peridynamics formulation for thermoplastic fracture[J].InternationalJournalofImpactEngineering,2016,87:83-94.
[15]黄丹,章青,乔丕忠,等.近场动力学方法及其应用[J].力学进展,2010,40(4):448-459.
[16]Lai X,Ren B,Fan H,et al.Peridynamics simulations of geomaterial fragmentation by impulse loads[J].InternationalJournalforNumerical&AnalyticalMethodsinGeomechanics,2015,39(12):1304-1330.
[17]Lai X,Liu L S,Liu Q W,et al.Slope stability analysis by peridynamic theory[J].AppliedMechanics&Materials,2015,744/745/746:584-588.
[18]Hughes T J R,Winget J.Finite rotation effects in numerical integration of rate constitutive equations arising in large-deformation analysis[J].InternationalJournalforNumericalMethodsinEngineering,1980,15(12):1862-1867.
[19]孙聪,李春光,郑宏,等.基于四边形网格的边坡上限有限元法[J].岩石力学与工程学报,2015,34(1):114-120.
[20]Lyamin A V,Sloan S W.Upper bound limit analysis using linear finite elements and non-linear programming[J].InternationalJournalforNumerical&AnalyticalMethodsinGeomechanics,2002,26(2):61-77.
[21]张鲁渝,刘东升,时卫民.扩展广义Drucker-Prager屈服准则在边坡稳定分析中的应用[J].岩土工程学报,2003,25(2):216-219.

