机载火控系统误差对精度影响的分析方法
胡子剑 高晓光 贺楚超 焦璐 尹登宇
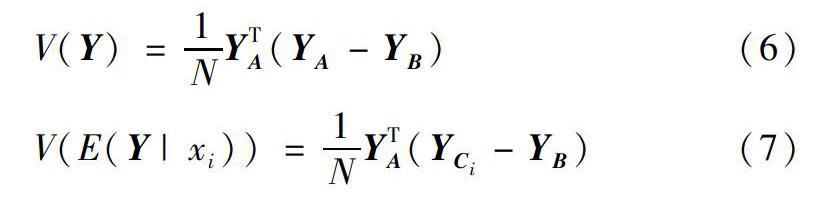
摘 要:本文讨论了机载火控系统精度的重要性, 针对直升机机载火控系统的精度问题, 应用Sobol指数法、 熵值法等常用的分析方法进行数据处理, 并比较各种方法的模型适应性、 计算量以及准确性, 在蒙特卡罗法的基础上提出了一种新的局部敏感性分析方法。
关键词: 机载火控系统; 误差分析; 敏感度分析; 熵值法; Sobol指数法; 蒙特卡罗法
中图分类号:TJ760.1; E926 文献标识码:A文章编号: 1673-5048(2018)05-0047-07[SQ0]
0 引言
机载火控系统具有任务准备、 导航、 搜索和攻击等重要作用。 工作时, 首先和地面指挥系统、 导引系统等各部分系统协同完成准备工作, 准备完成后进入导航阶段引导飞机飞向预定战区。 随后对目标进行搜索、 识别、 跟踪, 测定目标相对运动参数以及环境条件并发送给火控计算机, 火控计算后将瞄准信息和操控信息显示给飞行员进行瞄准发射, 完成攻击后引导飞机安全返航。 因此, 机载火控系统的精度对飞机在执行作战任务时能否准确地识别、 跟踪、 打击目标有直接影响。 由于机载航空火力控制系统试验非常昂贵, 因而需要根据少量的试验数据来对火控系统的精度进行评估, 以进一步减小系统误差, 提高系统精度。 现有的误差敏感性分析方法往往存在以下局限性: (1) 计算强度大, 步骤繁琐, 计算所需时间过长; (2) 对于同样的试验数据, 应用不同的分析方法所得到的结果不完全相同, 即各种方法的适用性及准确性存在差异; (3) 由于火控系统的不断发展, 技术水平不断提高, 一些先前的数据处理方法不再适用。
因此, 随着火控系统精度要求的提高, 需要改进以往的精度测量以及误差敏感性分析方法, 选择模型适用性最强的方法, 花费较小的代价减小火控系统误差。
1 敏感性分析方法
1.1 敏感性分析方法的分类
本文依据被研究的输入变量每次变化的数目将敏感性分析方法分为两类:
局部敏感性分析方法(local sensitivity analysis)和全局敏感性分析方法(global sensitivity analysis)。
在文献[1]的基础上将敏感性分析方法具体分类如图1所示。
文献[2-3]对各种方法的原理及优缺点进行了较为详细的介绍。 由于机载火控系统是一个复杂的非线性系统, 数学模型
比较复杂, 综合各种因素考虑, 本文主要采用熵值法和Sobol指数法分别对机载火控系统误差做局部敏感性分析和全局敏感性分析, 并在蒙特卡罗法的基础上提出一种新的局部敏感性分析方法。
1.2 熵值法
熵值法作为一种模型适用性较高的敏感性分析方法被广泛应用于各个领域。 其原理详见文献[4], 以下对仿真过程中所进行的数据处理步骤进行简要介绍。
(1) 首先对各指标数据进行归一化处理以消除量纲影响, 若影响因素与评价目标正相关, 则表明该影响因素为正向指标, 反之则为负向指标[4]。
正向指标的归一化处理:
X′ij=xij-xjminxjmax-xjmin(1)
负向指标的归一化处理:
X′ij=xmaxj-xijxjmax-xjmin(2)
式中xmaxj和xminj分别代表第j个指标值的最大值和最小值, xij为原数据样本值, X′ij为无量纲化后的数据样本值[5]。
(2) 计算第j项指标下第i方案指标值的比重Pij:
(3) 计算第j项指标的熵值ej:
其中k>0,ej≥0。 如果xij对于给定的j全部相等, 那么
此时ej取极大值, 即
(4) 计算第j项指标的差异性系數gj:
对于给定的第j项指标,xij的差异性越小, ej越大, 该项指标的敏感性越小; 反之 ej越小, 该项指标对于机载火控系统的圆概率误差所起的作用越大, 定义差异性系数:
航空兵器 2018年第5期
胡子剑, 等: 机载火控系统误差对精度影响的分析方法
则当 gj越大时, 指标的敏感性越大。
1.3 Sobol指数法
俄罗斯数学家Sobol I M于20世纪90年代提出了一种全局敏感性分析方法, 并以他的名字命名, 学者们称之为“Sobol 指数法”[6]。 该方法除了能够分析单个输入对输出的影响程度也就是单个输入的主效应指标, 还能分析多个输入的交互效应对模型输出的影响, 适用于机载火控系统这种多输入参数的复杂非线性系统。 文献[6]对Sobol指数法的原理进行了介绍, 本文简要介绍如何通过解析法进行敏感性指标计算。
如果分析问题函数的具体解析式可用数学公式表示, 而且各个输入变量的分布范围已知, 那么可以通过解析法直接计算各个输入的主效应指数、 全效应指数和输入间的高阶交互效应指数等敏感性指标。 但是在面对复杂大系统模型时, 分析函数不是具体的函数解析式而是由复杂的模型给出的, 这时就不能直接用解析法计算了, 而可以用蒙特卡罗法来计算敏感性指标。
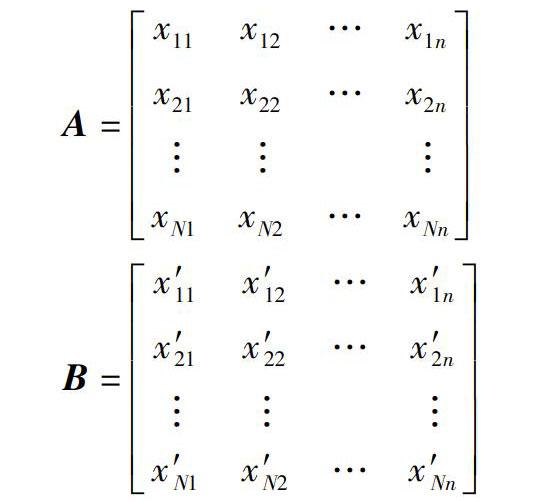
首先采用随机抽样的方法从输入参数的取值范围中随机产生输入参数的值, 并将这些输入参数按照元素的个数和样本次数生成两个相同大小输入参数矩阵A, B, 两个矩阵中每一行都是一组具体的输入参数组合, 每一个组合都可以通过模型计算得到其相应的输出。
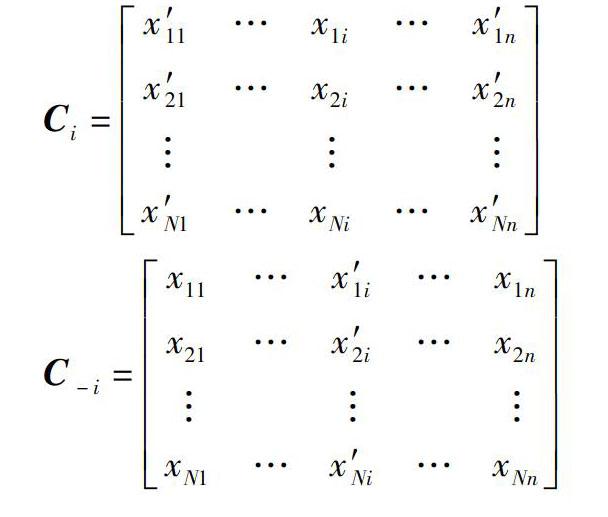
记Ci为将矩阵B的第i列换成矩阵A的第i列后的矩阵; 记C-i为将矩阵A的第i列换成矩阵B的第i列后的矩阵, 即
同理可定义Cij, C-ij, 将这些输入矩阵代入模型求解, 便可得到这些矩阵对应的模型输出向量。 YA, YB, YC 分别为相应的矩阵的输出列向量。 由蒙特卡罗法可得到以下估计:
则敏感性指标的估计的计算公式有如下表达。
输入变量Xi的主效应指数Sxi的估计为
输入变量Xi的全效应指数STxi的估计为
输入变量Xi和Xj的二阶交互效应指数Sxixj的估计为
采用蒙特卡罗法计算敏感性指标, 与直接计算相比有较高的精度。 该方法理论上适用于任何模型, 但是涉及到矩阵的运算, 实际计算量较大。
1.4 一种基于蒙特卡罗法的敏感性分析法
蒙特卡罗(Monte Carlo)方法, 也叫作计算机随机模拟方法, 是一种基于“随机数”的计算方法。 这种方法一般需要大量的实验来使数据分析结果更为准确和可靠, 实验次数越多, 误差就越小, 分析结果也就越可靠, 近年来高速电子计算机的出现和普及, 使这种方法被广泛应用于各个领域。
与Sobol指数法类似, 首先采用随机抽样的方法从输入参数的范围中随机产生输入参数的值, 并将这些输入参数按照元素的个数和样本次数生成一个输入参数矩阵Rij, Rij的每一行代表一组输入数据, 每一列对应一项输入参数, 并且每一组数据都可通过模型得到其对应的输出。 Rij对应的输出矩阵为C:
共有i组输入数据, 其中i的值越大, 估计结果的准确性就越高, 同时所需的计算量也就越大。
与熵值法采取的数据归一化方式不同, 这种方法并不单独进行归一化, 而是在计算的同时采用等比例变化的方法对数据进行处理, 从而使得不同数量级的输入参数之间可以进行比较。 以第n列为例, 令该列所有数据同时变化k, 其中k为变化比例, k越小, 即输入参数变化越微小, 分析结果越为可靠。 变化后的输入参数矩阵R′ij为
R′ij对应的输出矩阵为
计算按比例变化后的输出与原输出的差值ΔCn:
计算差值占原输出的比例并求其均值和方差:
均值En(ΔCn)反映了在其他输入参数不变的情况下, 第n个输入参数发生微小变化对系统输出结果的影响程度, 即敏感性En(ΔCn)越大, 则说明该参数对系统影响程度越大, 反之则说明敏感性较小, 均值的正负说明该影响因素与系统输出呈正相关或负相关, 在比较各输入因素之间的敏感性时按照其绝对值进行比较。
方差S2n(ΔCn)则反映了第n个输入参数在其可变范围内的敏感性稳定程度, 方差越大则说明稳定程度越差, 方差越小稳定性越好。
这种方法的优点在于: (1) 不需要进行复杂的数据归一化处理, 减小计算程度; (2) 操作简便, 易于应用; (3) 能够分析各输入参数的敏感性稳定程度, 即能够反映各参数在其变化范围内何处敏感性较大, 何处敏感性较小。
其局限性在于: (1) 为取得更为准确的敏感性分析结果, 需要大量的数据反复实验, 可能会增加计算量; (2) 由于分析微小变化所引起的影响, 对计算精度要求较高; (3) 无法分析各个输入参数之间的交互效应与互相的影响。
2 机载火控系统精度敏感性分析
2.1 机载火控系统精度敏感性分析的目的
火控系统精度的敏感性是指当各个误差源在其变化范围内变动时, 对整个火控系统精度的影响程度。 采用敏感性系数这一概念来描述影响程度, 即敏感性系数越大, 则该误差源对整个系统精度的影响程度就越大, 反之则影响程度较小。 分析机载火控系统精度的敏感性的主要目的是通过对火控系统各个误差源的分析, 得到各个误差源的敏感性系数或对火控系统精度的影响程度, 着重考虑敏感性系数较大的误差源, 并且忽略影响程度较小的误差源, 从而简化系统, 降低系统的复杂程度, 减少数据计算与分析比较时的工作量。 在提高机载火控系统精度的同时利用对各误差源的影响程度分析结果处理和解决实际的问题。
2.2 机载火控系统的误差源
机载无控武器如火箭彈、 航炮等的命中精度主要由机载火控系统的误差影响。 本文以直升机载火箭弹为例, 所研究的机载火控系统误差源主要有: 惯导测量误差、 挂架抖动误差、 传感器误差(雷达瞄准误差)以及环境误差(旋翼下洗流、 随机风)而且因为环境误差无法人为控制, 将其取为大小适当的定值, 其他未被考虑的误差源则均作为白噪声叠加在标准值上。 本文所研究的机载火控系统误差源关系如图2所示。
3 仿真计算和结果分析
3.1 仿真模型
本文主要研究基于航向坐标系[7]直升机火箭弹对地面目标进行攻击时各误差源对打击精度的影响程度。 直升机的机动状态为悬停状态, 采用连续计算命中点(CCIP)的瞄准原理, 如图3所示, 瞄准原理及公式等详见文献[8]。 其中O为武器投射点;C为武器命中点; H为攻击瞬间载机的高度; A为武器的无风射程矢量; U为风速矢量; W为载机的空速矢量; 为载机的俯冲角;VCH为瞄准线方位角; μCH为瞄准线俯仰角; ε为风向角; T为武器标准下落时间。
3.2 仿真分析模块与分析流程
本文对于直升机机载火控系统精度的分析流程分为参数生成模块和火控解算模块, 参数生成模块包括给定环境、 目标、 载机各参数初始值以及各部分误差的均方差值; 火控解算模块包括火控解算、 武器运动、 目标以及载机运动的数据处理, 见图4。
3.3 作战想定及参数设定
仿真时直升机的作战模式为悬停火箭弹对地攻击, 环境参数、 战术指标、 初始态势和仿真参数均见表1。
3.4 仿真结果
(1) 在熵值法分析时, 为避免出现无效数值的情况, 对归一化后的矩阵中的每一项进行加一处理, 即式(3)变为
熵值法的分析结果如表2所示。
由熵值法分析结果可知, 在不考虑各误差源之间的交互效应时, 各误差源的敏感性按对圆概率偏差的影响程度从大到小依次为: 惯导测量载机高度误差, 挂架抖动误差, 惯导测量载机偏航角
误差, 观瞄测量目标方位角误差, 观瞄测量目标距离误差, 风向角测量误差和风速测量误差。
(2) 采用基于蒙特卡罗的局部敏感性分析法分析后结果如表3所示。
蒙特卡罗法与熵值法的结果比较如图5所示。 从分析结果来看, 两种方法均指出在不考虑各误差源之间的交互效应的情况下, 对机载火控系统的圆概率误差影响程度最大的是惯导测量载机高度误差和挂架抖动误差, 风速测量误差和风向角测量误差的敏感性稍小, 其他三个误差源由于分析方法的不同其敏感性结果不完全相同但趋势一致。
但这种方法能够反映出各误差源的敏感性稳定程度, 如图6所示。
从结果来看, X4(观瞄测量目标方位角误差)的敏感性稳定性最差, 即该误差源可能在其变化范围内的不同参数点附近的敏感性不同且差异较大, 而其他误差源的敏感性稳定性则要远优于该误差源。
(3) Sobol指数法计算各误差源的全效应指数和主效应指数如表4和图7所示。
从全局敏感性分析方法Sobol指数法的分析结果来看, 与局部敏感性分析法的结果不同, 其主要原因是在分析时所有误差源的取值在其变化范围内同时变化, 各误差源之间的互相影响被考虑了进来。 无论从主效应指数和全效应指数来看, X2(惯导测量载机偏航角误差), X3(观瞄测量目标距离误差), X4(观瞄测量目标方位角误差), X5(风速测量误差)的指标值都较高, 表明在只考虑单一误差源不确定性单独对输出圆概率误差的贡献和同时考虑其他输入误差源之间的不确定性交互对输出圆概率误差的贡献的情况下, 这几个误差源的敏感度都较大, 对机载火控系统的精度误差影响较大, 而X7(挂架抖动误差)次之, 惯导测量载机高度误差的影响最小。
4 结论
直升機机载火控系统是一个非常复杂的非线性系统, 影响其精度的不确定因素有很多, 选择合适的灵敏度分析方法才能更好地解决实际问题, 减小误差, 提高精度。 本文对火控系统误差分析的三种方法各有利弊, 结果也不尽相同, 在考虑各输入因素之间的交互效应时采取Sobol指数法分析结果更为可靠, 在只考虑单一误差源的单独影响时可采用熵值法和本文在蒙特卡罗统计法的基础上提出的一种新方法。 该方法在样本数据足够大的情况下可以有效地对各误差源的敏感性稳定程序进行分析, 与熵值法相比, 此方法在已知误差的变化规律的情况下更有利于控制跟踪并减小和消除误差。具体问题应具体分析, 选择最适合系统的分析方法, 花费最小的代价, 更高效地解决实际问题。
参考文献:
[1] Ascough Ⅱ H C, Green T R, Ma L, et al. Key Criteria and Selection of Sensitivity Analysis Methods Applied to Matural Resource Models[C]∥ Modsim International Congress on Modeling and Simulation, Modeling and Simulation Society of Australia and New Zealand, Melbourne, Australia, 2005: 2463-2469.
[2] 傅攀峰, 周经伦, 罗鹏程, 等. 武器装备体系效能敏感性分析方法[J]. 火力与指挥控制, 2008, 33 (4): 58-60.
Fu Panfeng, Zhou Jinglun, Luo Pengcheng, et al. Sensitivity Analysis Method of System Effectiveness for Weapon and Equipment[J]. Fire Control and Command Control, 2008, 33 (4): 58-60. (in Chinese)
[3] 罗鹏程, 傅攀峰. 武器装备敏感性分析方法综述[J]. 计算机工程与设计, 2008, 29(21): 5546-5549.
Luo Pengcheng, Fu Panfeng. Review on Weapons and Equipment Sensitivity Analysis Methods[J] .Computer Engineering and Design, 2008, 29(21): 5546-5549. (in Chinese)
[4] 魏光辉, 陈亮亮, 董新光. 基于熵值与关联分析法的塔里木河下游区域水面蒸发影响因子敏感性研究 [J]. 沙漠与绿洲气象, 2014, 8(1): 66-69.
Wei Guanghui, Chen Liangliang, Dong Xinguang. Study on Sensitive Factors to Water Surface Evaporation in Tarim River Downstream Based on Entropy Value and Relational Analysis Method[J]. Desert and Oasis Meteorology, 2014,8(1): 66-69.(in Chinese)
[5] 段树国, 龚新蜀.基于熵值法的地区循环经济发展综合评价——以新疆为例[J]. 中国科技论坛, 2012(11): 98-103.
Duan Shuguo, Gong Xinshu.Comprehensive Evaluation of Regional Circular Economy Development Based on Entropy Method Taking XinJiang Province as an Example[J]. Forum on Science and Technology in China, 2012(11): 98-103.(in Chinese)
[6] Sobol I M. Sensitivity Estimates for Nonlinear Mathematical Models[J]. Mathematical Modeling & Computational Experiment, 1993(1): 407-414.
[7] 高曉光. 航空军用飞行器导论[M]. 西安: 西北工业大学出版社, 2004: 93-115.
Gao Xiaoguang. Introduction to Aviation Military Aircraft [M]. Xian:Northwestern Polytechnical University Press, 2004: 93-115.(in Chinese)
[8] 陆彦. 航空火力控制技术[M]. 西安: 西北工业大学出版社, 1989: 24-50, 221-226, 296-304.
Lu Yan. Aviation Fire Control Technology [M]. Xian: Northwestern Polytechnical University Press,1989: 24-50, 211-226, 296-304.(in Chinese)
Analysis Methods of the Impact on the Accuracy of
Airborne Fire Control Systems Error
Hu Zijian, Gao Xiaoguang, He Chuchao, Jiao Lu, Yin Dengyu
(School of Electronics and Information, Northwestern Polytechnical University, Xian 710129,China)
Abstract: This paper points out the importance of the accuracy of airbone fire control system.Aiming at the accuracy of helicopter airborne fire control system,some different analysis methods including Sobol method and Entropy method are used . The model adaptability, calculation and accuracy ofseveral methods are compared,anda new local sensitivity analysis method based on monte Carlo method is proposed.
Key words: airborne fire control system; error analysis; sensitivity analysis; Entropy method; Sobol method; Monte Carlo method

