高超声速飞行器控制输入时滞特性分析及主动鲁棒控制
秦伟伟 秦庆强 赵欣 扈晓翔 何兵 刘刚

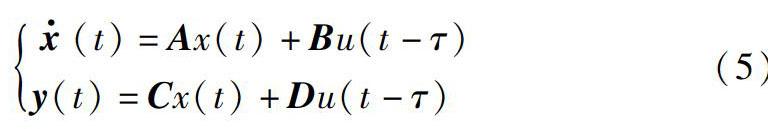
摘 要:本文研究了采用主动时滞补偿的主动鲁棒控制来解决高超声速飞行器的输入时滞问题。 由于高超声速飞行器的高动态特性, 使得系统存在强不确定性、 高非线性、 强耦合性、 输入时滞等问题, 控制系统的设计中存在许多难题。 因此, 设计一个能够克服时滞影响的控制算法是十分必要的。 本文首先采用频域方法分析了输入时滞特性影响; 然后, 基于超前预测的时滞补偿策略, 通过设计一个状态观测器对系统状态进行估计, 进而设计多步预测补偿算法来实现时滞补偿; 最后, 结合鲁棒控制方法提出了面向时滞补偿的高超声速飞行器主动鲁棒控制算法。 该种控制策略不仅可以解决参数模型的不确定性的鲁棒稳定性问题, 同时也保证了输入时滞情况下的系统状态稳定。 数值仿真的结果证实了该控制策略的有效性。
关键词: 高超声速飞行器; 输入时滞; 多步预测; 主动鲁棒控制
中圖分类号:TJ765; V249.1文献标识码:A 文章编号: 1673-5048(2018)05-0029-07[SQ0]
0 引言
与传统飞行器不同的是, 吸气式高超声速飞行器(AHFV)采用机体/发动机一体化设计使其飞行器的动力系统与控制系统以及机体结构之间的动态耦合性更强, 同时, 其大包线的飞行特点带来了飞行环境的复杂以及飞行器的气动和气热特性变化剧烈[1], 所以设计AHFV的飞行控制策略是一个极大的挑战。 为了保证稳定的飞行特性和飞行器的强鲁棒性, 针对AHFV非结构化线性化模型的不确定性, 采用鲁棒控制和鲁棒自适应控制等经典方法达到良好控制效果。 反馈线性化与神经网络、 滑模控制等控制方法分别结合形成的非线性控制器, 在非线性模型中也达到了良好的跟踪效果。 自适应技术和非线性控制技术在近几年也有了长足的发展, 自适应滑模控制[2]和基于逆鲁棒控制[3-4]等方法在非气动热模型中也多被提及。 在近期的科研工作中, 文献[5-7]中自适应控制算法被应用于控制高超声速飞行器, 文献[8]中提到非线性鲁棒自适应控制算法, 作者在气动热模型的基础上提出了一种基于李雅普诺夫稳定的跟踪控制器, 作为一种具有良好的控制效果和简单的设计过程的线性变参数化方法, 可以有效地将非线性模型转换为LPV模型, 并进行相应的分析和进一步设计, 因此该方法也得到了广泛的应用[9-12]。 近年来, 高超声速飞行器全飞行包线大跨度机动时,所面临的复杂动态特性成为了影响控制系统鲁棒性、 安全性、 快速性和精确性研究的热点问题[12-14]。 在高超声速飞行器大跨度机动飞行过程中, 未能探知的状态、 输出或控制时滞影响大大增加了控制系统的复杂性, 使其快速性、 精确性和安全性面临着更大的挑战。 对于飞行器的执行机构, 以升降舵为例, 它的偏转并不是理想的阶跃变化, 而是存在几十毫秒的上升延迟和下降延迟。 如果同时考虑信号传输及采样时延, 严重时将会造成0.1 s量级控制指令到轨迹生成的延迟。 对于飞行速度极高的高超声速飞行器来说, 这种延迟将导致姿态控制系统响应的快速性变差, 控制精度降低。 较大的姿态误差容易造成超燃冲压发动机工作状态异常, 轻则导致飞行器性能衰退, 重则引起飞行器解体。 显然, 在实施全飞行包线机动飞行时, 需要更加重视时滞动态对控制系统的影响。 但是, 现有关于高超声速飞行器控制系统的研究中, 极少考虑时滞影响。 时滞现象对高超声速飞行器控制系统的影响, 是亟待揭示的新问题, 如何消除或者降低时滞对控制系统的影响, 是当前亟需解决的新难题。
为此, 本文针对高超声速飞行器大跨度机动飞行时面临的控制输入时滞动态问题, 开展输入时滞影响分析及其主动鲁棒控制方法研究, 以保证控制系统在输入时滞情况下的系统状态稳定。
1 高超声速飞行器的输入时滞特性分析
1.1 高超声速飞行器的非线性模型
文献[5]中对高超声速飞行器模型进行进一步的研究, 将可变参数加入到纵向动力学运动方程中, 非线性方程描述如下:
式中: D为阻力; g为重力加速度; h为高度; Iyy为惯性矩; L为升力; M为俯仰力矩; m为飞行器质量; Q为俯仰率; q-为动压; S为参考截面积; T为推力; V为速度; γ为航迹倾角(γ=θ-α); θ为俯仰角; α为攻角。 其中, 力和力矩在本文控制模型中的近似表示如下:
这组模型包含五个变量, 分别是[V,α,h,θ,Q]。 在高超声速飞行器的纵向运动模型方程中, 输入控制信号Φ, δ c和δ e没有出现, 通过力与力矩T, L, D, M体现。 发动机动力学模型可以通过一个二阶系统展现:
1.2 高超声速飞行器输入时滞特性
从飞行器建模过程和分析可以看出, 高超声速飞行器模型具有强非线性、 强耦合性及气动参数和结构参数不确定等特点, 同时由于时滞要素的存在, 使得飞行器面临复杂动态影响, 而这些特点主要取决于飞行器自身固有的动力学特性。 为了深入理解飞行器固有的动态特性, 在开环条件下, 利用小扰动理论在平衡点处分别对刚体和弹性体非线性模型进行雅克比线性化, 得到线性状态空间方程, 获取系数矩阵的特征根和特征向量, 观察飞行器在给定平衡点处的运动模态。
飞行器的扰动运动模态能够反映运动变量随时间变化的规律以及各个变量之间的振幅比值和相位关系。 通常情况下, 飞行器的纵向扰动运动有两个模态, 即短周期模态和长周期模态, 了解模态特性就能对飞行器动态特性有更深刻的理解。 短周期模态主要表现在扰动恢复的初始阶段, 反映飞行器俯仰转动的特性, 主要是飞机俯仰角速度和攻角的变化, 速度的变化很小。 而长周期模态反映飞行器质心的运动特性, 主要是速度大小和俯仰角的周期性变化, 攻角的变化很小。 相对于长周期模态, 短周期模态衰减快、 振荡频率高, 长周期模态可在相当长的时间内起作用。 飞行器的纵向扰动运动及各运动参数随时间的变化即是由长周期模态和短周期模态的叠加而成。
1.2.1 无时滞动态特性分析
为分析刚体模型的运动模态, 在Matlab仿真环境下, 在高度h=85 000 ft和速度V=7 702 ft/s的条件下求取平衡点, 如表1所示。 在平衡点处对刚体非线性模型(1)进行小扰动线性化, 可以得到平衡点处高超声速飞行器的线性化模型。
进行线性化可得到此平衡点处的线性化方程, 描述为
其中, x=V,γ,h,α,QT, u=[Φ,δe,δc]T, y=[V,h]T。
更进一步, 求取线性状态空间方程系数矩阵的特征根, 得到刚体飞行器的开环极点及对应运动模态, 如表2所示, 零极点分布如图1所示, 其中控制输入为δe, 输出为速度h。
对于模型的极点, 首先, -2.780 8×10-15对应的是高度模态, 由于随着高度增加对于空气密度会有影响, 到高度上升到一定程度会出现一个不稳定的极点; 其次, -6.085 35和6.263 45是短周期模态, 两个短周期模态中有个一正根, 这直接导致高超声速飞行器线性模型不稳定; 再次, 特征根-0.000 003±0.000 015 1i代表的是长周期模态, 它们非常靠近坐标轴虚轴, 因此也极易不稳定。
显然, 此平衡点得到的线性模型具有不稳定和非最小相位特性, 因此需要设计一个控制器系统以保证高超声速飞行器在巡航段具有平稳迅速的机动控制性能。
1.2.2 包含时滞的动态特性分析
为分析刚体模型运动模态中的时滞特征影响, 在Matlab仿真环境下, 在高度h=85 000 ft和速度V=7 702 ft/s的条件下求取平衡点, 如表1所示。 在平衡点处对刚体非线性模型(1)进行小扰动线性化, 可以得到平衡点处高超声速飞行器的线性化模型。 更进一步, 考虑飞行器飞行过程中存在的输入时滞因素影响, 因此, 可以得到包含时滞动态的线性化模型如下:
x·(t)=Ax(t)+Bu(t-τ)y(t)=Cx(t)+Du(t-τ) (5)
根据Laplace变换的时域平移性质, 时滞传递函数与无时滞传递函数之间的数学关系描述如下:
G d(s)=G(s)e-τs(6)
其中, G d(s)为时滞系统传递函数;G(s)为无时滞系统传递函数。 这里为了简化问题研究的复杂度, 假设状态时滞是已知且是不变的, 即τ为常数。
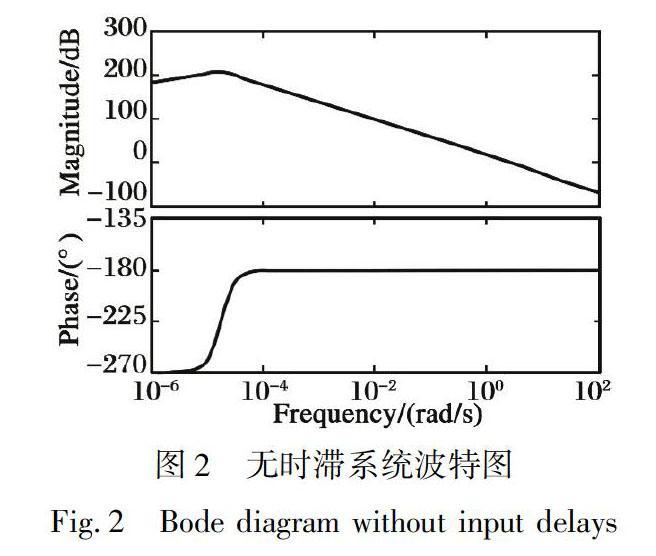
求取线性状态空间方程系数矩阵的特征根, 得到刚体飞行器的开环极点及对应运动模态和零极点分布, 其中控制输入为δe, 输出为速度h。 利用Matlab计算可知, 输入时滞对传递函数的零极点并没有什么影响, 这一点从传递函数上的变化亦可以得到。 但是, 其波特图发生了很大的变化, 特别是相位角裕度变化最为明显。 无时滞因素影响的频域波特图如图2所示, 包含输入时滞的频域波特图如图3所示。 其稳定裕度比较如表3所示。
对于上述系统而言, 该系统属于非最小相位系统, 负的相位裕度是不能确定稳定性的。 以上分析表明, 输入时滞的存在使得系统的相位裕度变化极其剧烈, 显然极大增加了控制系统的设计难度; 同时注意到幅值裕度有所增加, 因此如果能够采用时滞补偿, 有效克服时滞影响, 将可以有效提高系统的稳定性。
2 面向时滞补偿的高超声速飞行器主动鲁棒控制
2.1 基于超前预测的时滞补偿策略
基于上述分析, 本小节研究一种基于超前预测的时滞补偿策略。
2.1.1 时滞补偿策略
首先, 给出考虑输入时滞的离散线性化系统, 可以描述为
文献[15-16]中给出一种面向时滞系统的控制系统补偿算法。 通过设计一个状态观测器对系统状态进行估计, 然后设计多步预测补偿算法来实现时滞补偿。 其中, 预测输出采用了状态转移矩阵进行计算。 受此启发, 本文在文献[12]参数依赖鲁棒控制H∞控制的基础上, 设计一个基于时滞状态预测补偿的反馈控制器:
其中, x(k+τ k|k)表示在k时刻对状态在k+τk时刻的预测值。 该预测补偿控制器可以描述为如图4所示。
2.1.2 时滞补偿计算
基于上述τk-步时滞补偿策略, 这里采用当前时刻的标称线性化系统(A(k),B(k))迭代计算系统在k+τk时刻的状态值x(k+τk|k)。 因此可以得到状态预测计算过程如下所示:
更进一步:
因此, 可以将多步预测状态值作为当前的状态反馈量进行状态反馈控制, 从而有效补偿时滞影响。
2.2 基于时滞补偿的主动鲁棒控制策略
對于前一节提到的时滞补偿算法, 首先需要确定无时滞系统(以后成为标称系统)的状态反馈控制增益K(k)。 采用时滞补偿策略将(9)带入到系统状态方程, 由此可得到在设计k时刻的控制输入描述为
考虑输入时滞因素影响, 可得到
由此可得, 补偿后的闭环系统描述为
x(k+1)=Acl(k)x(k)(13)
其中,
A cl(k)=A(k)+B(k)K(k)(14)
显然, 通过构建基于状态转移矩阵的多步状态预测器实现了输入时滞的有效补偿。 通过反馈在k+τ k时刻的状态值x(k+τk|k), 可以将输入时滞系统描述成与文献[12]的标准模型相类似的形式, 因此可以直接利用参数依赖鲁棒H∞控制策略实现系统的控制, 算法稳定性证明这里不再赘述。
3 仿真与分析
通过大量的模拟实验来证明设计的控制方案的可行性。 给定高超声速飞行器的初始条件是在高度h 0=85 000 ft, 速度V 0=7 702 ft/s进行巡航段飞行。 要求高度h跟踪h c=1 000 ft的阶跃信号, 速度V跟踪Vc=100 ft/s的阶跃信号。
3.1 輸入时滞影响
首先, 本文重点对高超声速飞行器在飞行过程中的输入时滞影响展开研究。 针对文献[12]的鲁棒H ∞控制器, 假设控制系统中存在了0.3 s的状态时滞, 则其机动飞行过程的动态响应表现为如图5~8所示。
结果表明, 飞行器的状态未能完成给定的指令跟踪任务, 速度曲线出现了严重的误差, 导致了跟踪任务失败。 显然, 控制系统中存在的时滞因素严重影响了控制系统的性能,严重的甚至会造成
控制系统失稳, 引起灾难性的后果。 显然, 时滞要素是高超声速飞行器控制过程中不可避免的, 当达到一定值之后, 也将成为不可回避的关键问题。
3.2 基于时滞补偿的主动鲁棒控制策略
为考察本研究针对包含时滞的约束非线性系统设计的基于时滞补偿的参数依赖鲁棒H∞控制策略的有效性。 利用基于时滞补偿的参数依赖鲁棒H∞控制策略对包含0.3 s输入时滞的系统实施控制。 具体仿真条件设置如下: 在其他条件不变的情况下, 假设高超声速飞行器初始平衡条件为V0=7 702 ft/s, h0=85 000 ft, 从0时刻开始高超声速飞行器跟踪给定速度和高度参考指令Vr, hr进行机动飞行, 以实现Vc=100 ft/s, hc=1 000 ft跟踪控制目标, 则其机动飞行过程的动态响应表现为如图9~11所示。
结果表明, 在存在输入时滞的情况下, 控制系统实现了很好的速度和高度跟踪, 有效抵消了输入时滞所带来的影响。 同时, 通过图9~10可以看出, 闭环系统可以将跟踪误差控制在很小的范围内, 并且最终趋于零。 图11给出了重要的几个参数的变化曲线。 其中, 攻角的变化范围为±5°以内。 同时, 升降舵和发动机参数的变化范围也是合理有效的。 因此, 本文在文献[12]参数依赖鲁棒H∞控制策略的基础上, 通过设计时滞状态预测补偿器, 进而提出的基于时滞补偿的参数依赖鲁棒H∞控制策略能够有效克服高超声速飞行器大范围机动中所面临非线性、 非最小相位系统和输入时滞等复杂动态影响, 取得了很好的控制效果, 具有良好的实际效果。
参考文献:
[1] Mirmirani M, Wu C, Clark A, et al. Modeling for Control of a Generic Airbreathing Hypersonic Vehicle[C]∥AIAA Guidance, Navigation, and Control Conference and Exhibit, San Francisco, Carolina, 2005.
[2] Wang Q, Stengel R F. Robust Nonlinear Control of a Hypersonic Aircraft[C]∥AIAA Guidance, Navigation, and Control Conference and Exhibit, Porland, OR, 1999:413-423.
[3] Xu H J, Mirmirani M, Ioannou P A. Robust Neural Adaptive Control of a Hypersonic Aircraft[C]∥AIAA Guidance, Navigation, and Control Conference and Exhibit, Austin, Texas, 2003: 1-8.
[4] Xu H J, Ioannou P A, Mirmirani M. Adaptive Sliding Mode Control Design for a Hypersonic Flight Vehicle[J]. Journal of Guidance, Control and Dynamics, 2004, 27(5): 829-838.
[5] Parker J T, Serrani A, Yurkovich S, et al. Control Oriented Modeling of an Air Breathing Hypersonic Vehicle[J]. Journal of Guidance, Control, and Dynamics, 2007,30 (3): 856-869.
[6] Fiorentini L, Serrani A, Bolender M A, et al. Nonlinear Robust / Adaptive Controller Design for an Air Breathing Hypersonic Vehicle Model[C]∥AIAA Guidance, Navigation, and Control Conference and Exhibit, Hilton Head, South Carolina, 2007: 1-16.
[7] Fiorentini L,Serrani A,Bolender M A, et al. Nonlinear Robust Adaptive Control of Flexible Air Breathing Hypersonic Vehicles[J]. Journal of Guidance, Control, and Dynamics, 2009, 32(2): 401-416.
[8] Wilcox Z D, MacKunis W, Bhat S, et al. Lyapunov Based Exponential Tracking Control of a Hypersonic Aircraft with Aero Thermoelastic Effects[J]. Journal of Guidance, Control, and Dynamics, 2010,33(4): 1213-1224.
[9] Groves K P, Serrani A, Yurkovich S, et al. Anti Windup Control for an Air Breathing Hypersonic Vehicle Model[C]∥AIAA Guidance, Navigation, and Control Confe rence and Exhibit, Keystone, Colorado, 2006.
[10] Petersen C, Baldwiny M, Kolmanovsky I. Model Predictive Control Guidance with Extended Command Governor Inner Loop Flight Control for Hypersonic Vehicles[C]∥AIAA Guidance, Navigation, and Control (GNC) Conference, Boston, MA, 2013.
[11] Qin Weiwei, Liu Jieyu, Liu Gang, et al. Robust Parameter Dependent Receding Horizon H∞Control of Flexible Air Breathing Hypersonic Vehicles with Input Constraints[J]. Asian Journal of Control, 2015, 17(2): 508-522.
[12] 秦偉伟, 刘刚, 汪立新, 等. 基于参数依赖滚动时域H∞控制的高超声速飞行器控制[J]. 控制与决策, 2014, 29(3): 403-410.
Qin Weiwei, Liu Gang, Wang Lixin, et al. Parameter Dependent Receding Horizon H∞ Control for a Hypersonic Vehicle[J]. Control and Decision, 2014, 29(3): 403-410. (in Chinese)
[13] Jiang Wei, Wang Hongli, Lu Jinghui, et al. HOSVD Based LPV Modeling and Mixed Robust H2/H∞ Control for Air Breathing Hypersonic Vehicle [J]. Journal of Systems Engineering and Electronics, 2016, 27(1): 183-191.
[14] 张广豪, 郭宏宇, 秦伟伟, 等. 基于PD-RMPC算法解决弹性体高超声速飞行器的输入饱和与状态约束问题[J]. 航空兵器, 2017(3): 33- 44.
Zhang Guanghao, Guo Hongyu, Qin Weiwei, et al. PD-RMPC for a Flexible Air Breathing Hypersonic Vehicle with Input Saturation and State Constraints[J]. Aero Weaponry, 2017(3): 33- 44. (in Chinese)
[15] Luck R, Ray A. An Observer Based Compensator for Distributed Delays [J]. Automatica, 1999, 26(5): 903-908.
[16] Liu H, Brandel F. Compensator Design for Large Time Delay in a Flight Control System[C]∥AIAA Guidance, Navigation, and Control Conference and Exhibit, 2004.
Input Time Delay Characteristic Analysis and Active Robust
Control for an Air Breathing Hypersonic Vehicle
Qin Weiwei1, Qin Qingqiang2, Zhao Xin1,Hu Xiaoxiang1, He Bing1, Liu Gang1
(1. Rocket Force University of Engineering, Xian 710025, China;
2. Weapon Office at CETC of Rocket Force, Beijing 101025, China)
Abstract: The design of active robust controller based on delay state compensation for a class of flexible air breathing hypersonic vehicles with input delays is describedin this paper. Due to the high dynamic characteristics of hypersonic vehicle,
the strong uncertainties, high nonlinearity, strong coupling, and control input time delays are challenging problems in the design of its control system. Therefore,
it is necessary to design a control method that can handle input time delays. Firstly, the frequency domain method is used to analysis the influence of the input time delays.
Based on the time delay compensation strategy of advance prediction, a state observer is designed to estimate the system state, and then a multi step predictive compensation algorithm is designed to compensate the time delays. Finally, an active robust control algorithm for hypersonic vehicle with time delay compensation is proposed. This control strategy can not only solve the problem of robust stability of parametric model uncertainties, but also ensure the stability of the system with input delays. Numerical simulation results confirm the effectiveness of the control strategy.
Key words:hypersonic vehicle; input delays; multi step prediction; active robust control

