钢管混凝土贯通横隔板梁柱节点有限元分析及结果影响因素探讨
,,
(1.湖南省高速公路管理局,湖南 长沙 410000; 2.江苏省武警总队,江苏 南京 210000;3.上海交通大学 船舶海洋与建筑工程学院,上海 200240)
0 引言
钢管混凝土结构自19世纪末首次在美国出现后,因其强大的承压能力和良好的抗震性能,在高层建筑、地铁车站,尤其是大跨度桥梁工程中在世界范围内得到了日益广泛的应用。钢管混凝土梁柱节点是钢管混凝土结构体系的重要组成部分,它主要传递梁端剪力和弯矩(刚性节点)或仅传递梁端剪力(铰接节点)。随着钢管混凝土结构在土建工程中的广泛应用,很多新的节点构造形式被创造出来。比如外环板式、內隔板式、环板贯通式、端板螺栓式、栓钉锚固式、铰接节点等[1-5]。
在大量试验数据的基础上辅之以有限元分析,既可以对数值模拟的准确性加以掌握,又可以利用有限元分析丰富的后处理对有限的试验数据予以扩充、细化和形象化,能够更深入广泛地认识梁柱节点模型的各种力学性能[6-10]。哈尔滨工业大学的韩晓健等对钢筋混凝土双梁夹柱穿心承重销的梁柱节点进行了模型试验和有限元三维受力分析[11];同济大学的陈曦等论述了5种本构模型在钢管混凝土短柱轴压承载力有限元分析中的特点[12];福州大学的宗周红等对方钢管混凝土柱与钢梁连接节点在低周反复荷载作用下的滞回性能进行了非线性分析计算[13];兰州大学的史艳莉等对内置十字钢骨圆钢管混凝土构件的受弯性能试验进行有限元模拟[14]。这些研究成果从不同的方面讨论了有限元分析在钢管混凝土研究里的应用,但他们对影响有限元分析结果的因素方面讨论还不完善[14-17]。
贯通横隔板加强钢管混凝土结构梁柱立体节点是环板贯通式节点的一种具体结构形式。针对此种节点,作者设计了专门试验对其力学特性进行了试验研究[18]。本文在该试验结果的基础上,采用贯通横隔板梁柱立体节点试验构件的真实材料性质和实际加载情况,建立有限元模型进行数值模拟计算。在验证了有限元方法可行性的基础上,对影响有限元计算结果的因素进行了探讨。
1 梁柱节点加载试验
1.1 试验方案
试验对象为Test—1、Test—2这2个钢管混凝土梁柱节点。柱钢管外径均为D=406.4 mm;管壁厚分别为9 mm和12 mm;贯通横隔板的内圆直径为d=320 mm;横梁采用焊接H型钢,尺寸为H—400 mm×200 mm×9 mm×19 mm。上述3个部件的材料均为SM490(日本钢材牌号,相当于国内的Q345)。柱填充混凝土的设计基准强度为17.7 N/mm2。为防止节点横梁的面外变形,分别在横梁A、B和C、D之间连接了尺寸为200 mm×100 mm×9 mm×9 mm的斜梁,材料为SM490。
所使用的填充混凝土和钢材的机械性能如表1和表2所示。
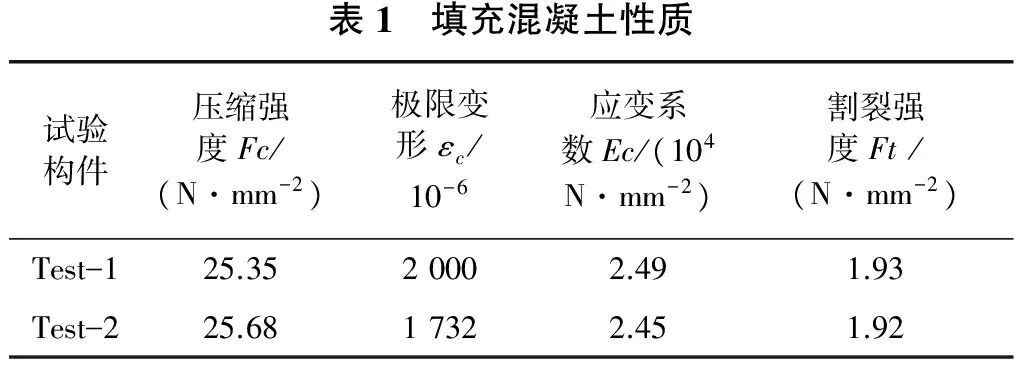
表1 填充混凝土性质试验构件压缩强度Fc/(N·mm-2)极限变形εc/10-6应变系数Ec/(104N·mm-2)割裂强度Ft/(N·mm-2)Test—125.3520002.491.93Test—225.6817322.451.92
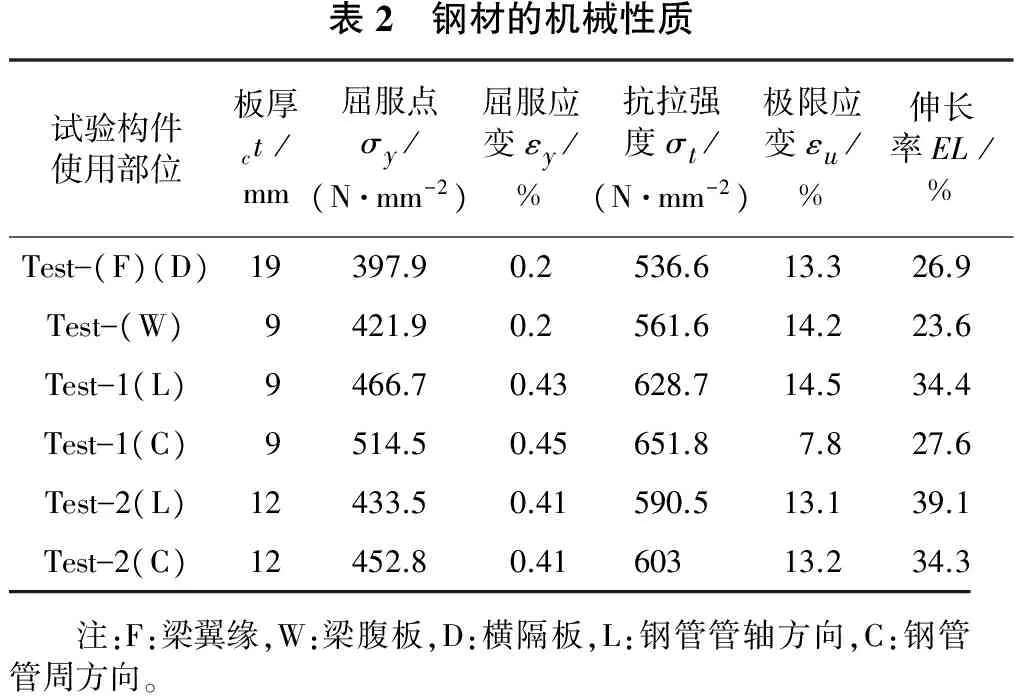
表2 钢材的机械性质试验构件使用部位板厚ct/mm屈服点σy/(N·mm-2)屈服应变εy/%抗拉强度σt/(N·mm-2)极限应变εu/%伸长率EL/%Test—(F)(D)19397.90.2536.613.326.9Test—(W)9421.90.2561.614.223.6Test—1(L)9466.70.43628.714.534.4Test—1(C)9514.50.45651.87.827.6Test—2(L)12433.50.41590.513.139.1Test—2(C)12452.80.4160313.234.3 注:F:梁翼缘,W:梁腹板,D:横隔板,L:钢管管轴方向,C:钢管管周方向。
试验装置如图1所示,柱头和柱脚分别采用滚轴支座和铰接支座,由横梁上连动的A、B和C、D点4个同步油压千斤顶(性能为:最大荷载为±4.9×106N,千斤顶行程为±15 cm)进行同步连续加载。
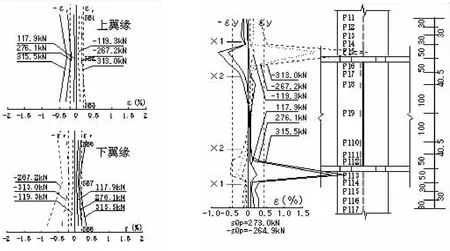
图1 试验装置
这样能保证在梁柱空间节点斜45°方向上再现反复荷载作用下的应力状态。整个加载过程没有考虑柱轴向荷载的作用。以斜45°方向的层间位移角作为反复加载的控制目标。构件斜45°方向的层间位移角RT目标值分别为:±0.005、 ±0.01、±0.015、±0.02、±0.025、±0.03、±0.04、±0.05 rad,对每个控制值的层间位移角分别作3周的反复加载循环。
1.2 试验结果

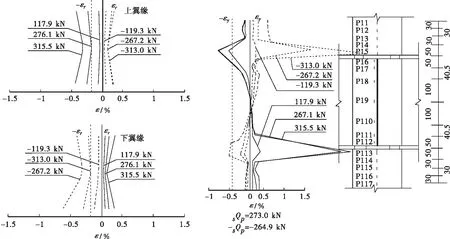
图2 应变分布图(尺寸单位: cm)
试验构件Test—1,当RT=0.012 rad附近时首先节点域剪切屈服,接着柱端节点钢管开始弯曲屈服;当RT=0.019 rad附近时,梁翼缘张拉侧及压缩侧梁柱节点局部屈服,柱钢管壁的面外屈曲和填充混凝土的局部压缩明显增大;之后,梁翼缘开始发生全面屈服;当RT=0.04 rad附近时,贯通横隔板与梁张拉翼缘连接角部出现细微的开裂,这些裂缝一直扩展到试验的最终阶段;当RT=0.05 rad时,在加载的第1周期柱端节点处钢管壁发生开裂,这样的裂缝在加载的第2周期有显著扩展,同时受压侧柱钢管局部屈曲,开始屈服破坏。
试验构件Test—2,当RT=0.014 rad附近时,首先节点域剪切屈服,接着柱端节点钢管开始弯曲屈服;当RT=0.017 rad附近时,梁翼缘张拉侧梁柱节点局部屈服,柱钢管壁的面外弯曲明显;大致同时,梁翼缘开始发生全面屈服;当RT=0.04 rad附近时贯通横隔板与梁翼缘张拉侧连接角部出现细微的开裂;当RT=0.08 rad附近时有明显扩展并且达到最大强度。
2 有限元分析
2.1 建模
本文模拟计算采用通用有限元分析程序ANSYS。由于柱钢管管壁较厚,为了能较准确地模拟实际情况,本文试验构件模型中柱钢管、贯通横隔板、梁翼缘及腹板和填充混凝土均采用实体单元SOLID45建模。为了反映加载过程中填充混凝土与柱钢管管壁之间的接触和脱离,采用了三维面-面接触单元 CONTA174 和 TARGE170。考虑到试件上不施加轴向力,所以对钢管与混凝土之间的粘结与摩擦不予考虑。
考虑钢材料的性状,为增强模型计算的收敛性,本文采用多线性弹性材料模型。分析中采用的屈服准则为Von Mises 准则。使用DP材料来模拟混凝土,没有考虑混凝土由于屈服引起的体积膨胀,即膨胀角φf=0。DP材料的另外两个材料特性值粘聚力及内摩擦角由单轴拉伸及压缩的试验数据得到。
为了保证求解精度,全部采用四面体单元。梁翼缘与钢管节点域是应力梯度较大的区域,也是本文计算所关注的区域,因此对其附近的钢材和填充混凝土网格适当加密。试验构件Test—1的有限元模型(FEM)中节点总数为21 573,实体单元SOLID45总数为67 457,接触单元中TARGE170总数为6 084、CONTA174总数为2 208;试验构件Test—2的有限元模型(FEM)中节点总数为20569,单元总数为49576,接触单元中TARGE170总数为3644、CONTA174总数为1428。考虑到斜梁只起到辅助支撑的作用,为了节省CPU时间和硬盘空间,此处建模不包括斜梁。所建分析模型如图3所示。
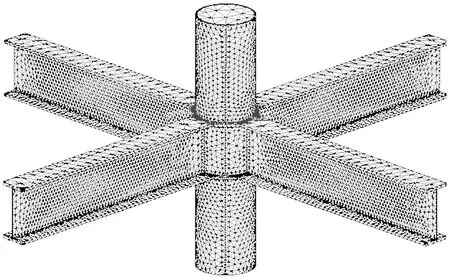
图3 有限元分析模型
由试验结果可以知道两试验构件在层间位移角RT等于0.012 rad和0.014 rad附近时节点域分别开始屈服,考虑到非线性问题(接触非线性和材料非线性)的复杂性,本文只研究了有限元模型在小应力应变状态下多步荷载作用的模拟计算。在钢管混凝土下端施加位移约束,在钢管混凝土上端钢管边缘施加X、Y方向约束,对钢管混凝土上端Z方向的位移不施加约束。
2.2 分析结果
2.2.1 变形
有限元模型Test—1和Test—2在荷载作用下的局部变形比较相似,如图4所示。从有限元模型的变形图中可以观察到在受拉侧翼缘处柱钢管壁有较大的面外变形,而受压侧翼缘处柱钢管的面外变形则不明显。节点的最大位移发生在横梁远离节点端处,且节点层间位移越大,节点的变形也越大。这与实验结果相符,因为在荷载较小的情况下2个试验构件的试验结果也基本差不多。
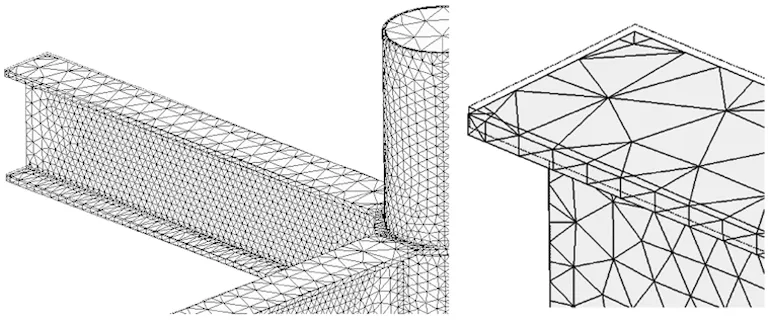
图4 局部变形
2.2.2 节点应变分布
构件Test—1的梁上、下翼缘及柱钢管管壁沿轴向在不同荷载作用下的应变分布如图5所示。上翼缘图中右侧曲线为负向层间位移作用时的拉应变,左侧曲线为正向层间位移作用时的压应变;下翼缘图中右侧曲线为正向层间位移作用时的拉应变,左侧曲线为负向层间位移作用时的压应变;柱钢管管壁只考虑了试验构件受正向层间位移侧柱钢管沿轴向的应变分布。
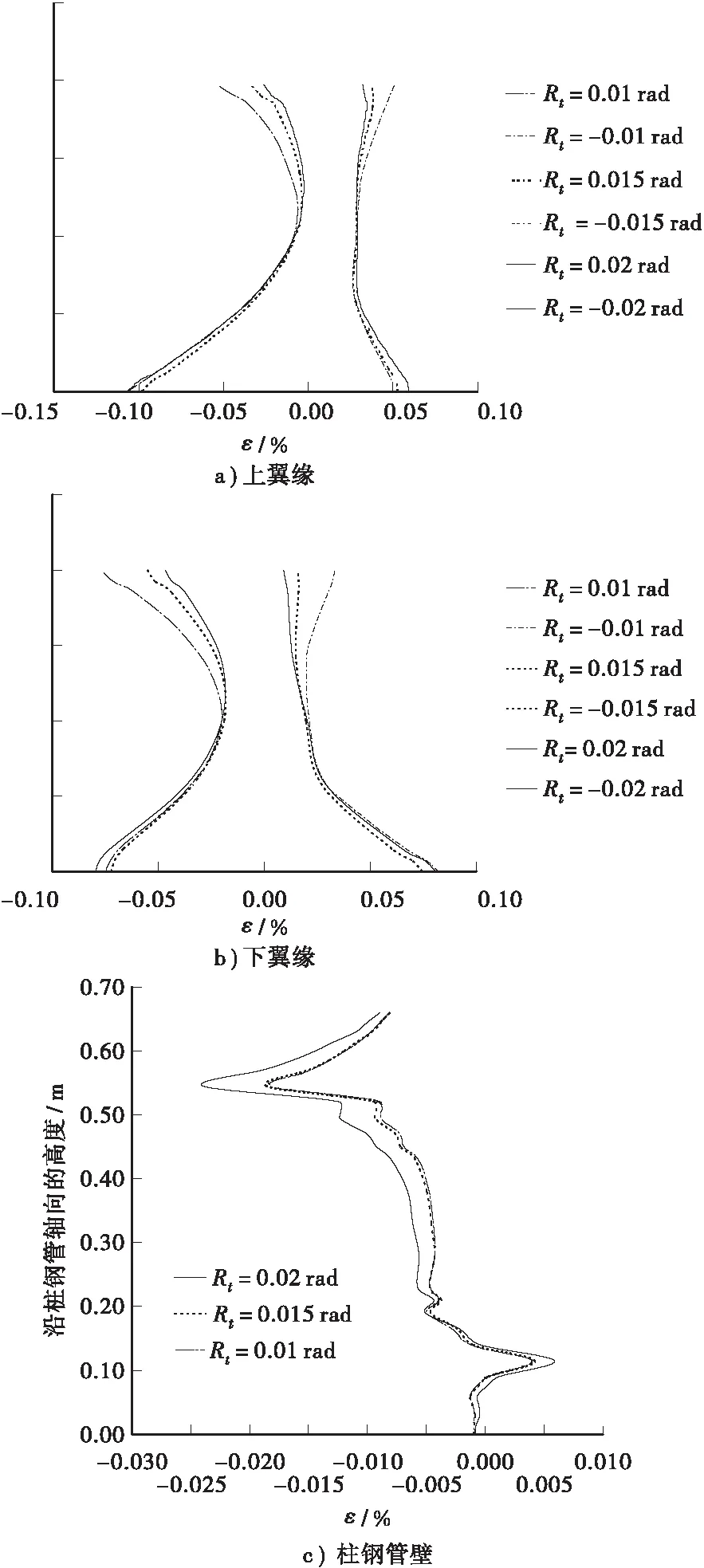
图5 应变分布图
比较图2与图5可看出,有限元计算所得的应变分布与试验构件的实验所得的应变分布比较接近。在梁上翼缘位置处,柱钢管沿轴向的应变分布表现为压应变;而在梁下翼缘位置处,柱钢管沿轴向的应变分布表现为拉应变。拉压应变的最大值分别出现在下翼缘和上翼缘的中线附近处;梁翼缘断面边缘处的应变比中间处的应变要大。对于不同的层间位移,基本符合层间位移角越大拉、压应变也表现得越大。均与试验结果相符。
从图中还可以得到,上翼缘断面两侧边缘的应变值不等,靠近节点域一侧的应变要小于靠非节点域一侧的应变。分析其原因是由于模型中未考虑支撑斜梁的作用,致使横梁产生了面外变形,从而使上翼缘一侧应变增大,另一侧应变减小。
3 影响有限元数值模拟结果的因素
上面的分析说明有限元能较好地模拟试验过程。在模拟过程中,有些因素对最终的模拟结果会产生较大的影响。
3.1 有限元模型对结果的影响
前文未考虑支撑斜梁的影响,在此建立了斜梁的有限元模型,如图6。模型中是否包含支撑斜梁对梁端上翼缘应变分布影响的结果如图7所示。

图6 加支撑斜梁的有限元模型

图7 FEM模型对节点梁端应变分布的影响
显而易见,支撑斜梁对横梁的面外变形有很大影响,有斜梁(LL—Y)时,梁端翼缘的应变分布基本是以中线为对称轴的标准抛物线;而无斜梁(LL—N)时,梁端翼缘靠近非节点域侧的应变要大于靠近节点域侧的应变,且抛物线的顶点也偏离了翼缘中间位置。
3.2 约束条件对结果的影响
在有限元模拟计算中一个重要的影响因素是约束条件。本文以有连接梁的试验构件Test—1为基本有限元模型,在柱钢管下端施加不同的约束条件,分别是面约束(P)和反对称面下端线约束(L),考察了约束条件对柱钢管轴向应变的影响,结果如图8所示。

图8 约束条件对柱钢管轴向应变的影响
从图中可以得到,无论是靠近上翼缘侧柱钢管所受的压应变还是靠近下翼缘侧柱钢管所受的拉应变,在柱钢管下端受面约束时数值比较大,原因是在这种约束条件下柱钢管下端不能转动。
3.3 网格划分精度对结果的影响
有限元计算对网格划分的密度和形状都有相当的要求,否则不仅结果难以达到合理的精度,有时还会出现错误的结果,甚至计算不能收敛。
通过对不同的网格划分密度进行试算,可以获得一个相对收敛的解答。此时,应力和应变等导出量的ELEMENT SOLUTION(单元解,根据每个单元的应变和应力矩阵得到)和NODAL SOLUTION(节点解,节点相邻单元的解答平均后得到)应该趋于一致。
本文中各试件有限元模拟的解在整个加载过程中相应位置处的Von Mises等效应力的单元解和节点解保持了较好的一致性,说明本文所关注的区域的网格密度可以满足对计算精度的要求。
3.4 非线性求解参数对结果的影响
本文计算中涉及到了材料非线性和状态非线性(接触非线性),因此相应的非线性求解控制参数对结果的合理性起着举足轻重的作用。分析和试算发现,荷载的增量步长、接触刚度和单元的积分方法是3个比较重要的影响因素,综合调整这几个参数使结果达到收敛是进一步评价结果是否准确的前提。
加载路径对非线性分析的影响是显而易见的,并且钢管混凝土结构和纯钢结构不同,由于接触问题的存在,在加载的起始阶段就是一个状态非线性的问题。如果荷载增量取得太大,不仅该步的迭代求解可能出现偏差,甚至会由于接触状态(包括法向的穿透和切向的滑移)发生较为剧烈变化和振荡造成难以收敛。在此时相对较小的增量步长将有助于接触状态的平缓变化和接触力的平稳传递。
接触刚度的影响就更为复杂一些,所有的接触问题都需要定义接触刚度,为了保证界面之间的穿透量足够小,接触刚度必须足够大,但是过大的刚度又会带来矩阵的病态和问题的收敛困难,特别是对于迭代求解器。一般来讲,应该选取足够大的接触刚度以保证接触渗透小到可以接受,但同时又应该让接触刚度足够小以使不会引起总刚矩阵的病态问题而保证收敛性。实际问题中只能通过不断的试算来确定一个合适的接触刚度。
就单元的积分方法而言,在非线性分析中使用减缩积分的方法不仅有助于节省CPU时间和硬盘空间,更重要的是可以避免体积锁死,并且相对于精确积分的方法有着更好的收敛性能,但其计算结果的精度需要仔细校核。
4 结论
1) 有限元分析法能较好地模拟钢管混凝土梁柱节点的实际加载过程,并给出比较可靠的分析结果。
2) 在建立有限元分析模型时,有些构造细节不能随意简化,否则会严重影响分析结果。
3) 设定约束条件时,应仔细分析实际约束状态,要保证提取的约束形式与实际边界条件尽量相符。
4) 网格划分并非越细越好,更不能盲目追求全结构划分的均匀性,应根据结构的受力特性合理地确定不同区域的网格划分精度。以保证有限元模拟的解在整个加载过程中相应位置处的Von Mises等效应力的单元解和节点解保持较好的一致性。
5) 荷载的增量步长、接触刚度和单元的积分方法是非线性求解控制参数中3个比较重要的影响因素,综合调整这几个参数使结果达到收敛是进一步评价结果是否准确的前提。
[1] 钟善桐.钢管混凝土结构(第3版)[M].北京:清华大学出版社,2003.
[2] 严国敏.钢管混凝土组合桥墩高架桥的设计与实施──日本新干线高架桥的快速施工[J].世界桥梁,1999(1):42-44.
[3] 日本建築学会.コンクリート充填鋼管構造設計施工指針[Z].1997.
[4] 付功义,森田耕次,等.コンクリート充填角形鋼管柱-合成梁偏心部分骨組架構の力学的舉動[A].第2回鋼構造年次論文報告集[C].1994.
[5] 付功义,森田耕次,等.コンクリート充填圆形鋼管柱-鐵骨梁立体部分骨組架構における柱梁结合部の力学舉動に關する研究[A].日本建筑学会構造系論文集[C].1998,第508号.
[6] 钱稼茹,崔瑶,方小丹.钢管混凝土柱受剪承载力试验[J].土木工程学报,2007,40(5):1-9.
[7] 李斌,任利民.矩形钢管混凝土框架结构受力性能试验研究[J].工程力学,2009,38(2):103-107.
[8] 谷利雄,丁发兴,付磊,等:圆端形钢管混凝土轴压短柱受力性能研究[J].中国公路学报,2014,27(1):57-63.
[9] 聂建国,胡红松,李盛勇,等.方钢管混凝土暗柱内嵌钢板-混凝土组合剪力墙抗震性能试验研究[J].建筑结构学报,2013,34(1):52-60.
[10] 向黎明,吕西林.高层钢管混凝土结构节点形式的介绍[J].结构工程师,2000(4):1-5.
[11] 韩晓健,孙伟民.钢管混凝土柱节点三维有限元受力分析[J].南京建筑工程学院学报(自然科学版),2001(4):79-83.
[12] 陈曦,周德源.五种本构模型在钢管混凝土有限元中的比较[J].工程力学,2009,26(6):116-121.
[13] 宗周红,葛继平,杨强跃.反复荷载作用下方钢管混凝土柱与钢梁连接节点非线性有限元分析[J].建筑结构学报,2006,27(2):75-81.
[14] 史艳莉,张海龙,王文达,等.内置十字钢骨圆钢管混凝土构件受弯性能有限元分析[J].建筑结构学报,2015,36(S1):318-323.
[15] 吴庆雄,陈宝春,韦建刚.钢管混凝土结构材料非线性的一种有限元分析方法[J].工程力学,2008,25(6):68-74.
[16] 夏铎,徐彬.钢管混凝土柱新型节点的有限元分析[J].昆明理工大学学报(自然科学版),2001,26(5):4-7.
[17] 张广泰,韩建红,荣彬.隔板贯通式钢管混凝土节点有限元分析[J].建筑钢结构进展,2016,18(2):26-33.
[18] 肖薇薇,高海健,付功义.钢管混凝土贯通横隔板力学特性试验研究[J].湖南交通科技,2017(3):145-148,196.

