高中立体几何常见题型及解题技巧

☉河北省武安市第一中学 李潇阳

空间图形问题经常转化为平面问题，而这种转化又是空间图形中解决问题的重要思想方法.利用直线与直线的位置关系，研究直线与平面的位置关系，利用直线与平面的位置关系研究平面与平面的位置关系，反过来，由平面与平面位置关系又可进一步掌握直线与平面的位置关系，由直线与平面、平面与平面的位置关系又可进一步确定直线与直线的位置关系.一般情况下，高中立体几何的题型在解析中都具有一定的规律.在解填空题时，可以采用排除法、直接计算法等多种方法来进行解题.在实际运用中，有时需要采用多种不同的解题方法，以提高立体几何的解题效率和正确率.

一、高中立体几何的基础知识整合

平行和垂直是空间中两种重要的位置关系，平行关系、垂直关系是其他位置关系的基础，在线线平行与垂直、线面平行与垂直、面面平行与垂直这些位置关系中，线面平行与垂直起着承上启下的作用.因为它蕴含着平移，线线平行（或垂直）、面面平行（或垂直）相互转化，空间问题与平面问题相互转化.

由上表可见，线线平行（垂直）、线面平行（垂直）、面面平行（垂直）是可以相互转化与化归的，通过转化可以实现降维.

1.线面、面面平行的证明方法

证明线面平行常用方法有：（1）定义法：线面没有公共点；（2）线面平行的判定定理；（3）面面平行的性质定理.

在解题时，一般运用后两者.在判定两个平面是否平行时，首先需要对线线平行以及线面平行的问题进行考虑［1］.可以根据定义来判定两个平面是否有公共点.此外，还可以根据面面平行的判定定理来判断.

2.线面、面面垂直的证明方法

证明线面垂直常用方法有：（1）定义法：一条直线垂直于平面内任意一条直线，则这条直线垂直于平面；（2）线面垂直的判定定理；（3）面面垂直的性质定理.

在解题过程中，一般常用后两者，尤其是性质定理的合理使用会显著提升解题的效率.

3.空间角的计算方法

空间角包括异面直线所成角、线面角、二面角，在计算空间角时，可以利用降维的思想方法，首先通过平移得到平面角，然后借助平面几何的知识解三角形求出角的大小.

二、高中立体几何常见题型的解题案例分析

1.立体几何选择题的解题技巧

例1（2012年陕西卷）已知六棱锥P—ABCDEF的底面是正六边形，如图1，PA⊥平面ABC，PA=2AB，则下列结论正确的是（ ）.

（A）PB⊥AD

（B）面PAB⊥平面PBC

（C）直线BC∥平面PAE

（D）直线PD与平面ABC所成角为45°

图1

解析：本题的四个选项分别给出了线线垂直、面面垂直、线面平行和线面角的判定，重点考查了三垂线定理及线面角，其每一个选项的设计都考查了学生的逻辑思维能力.这类题是历年高考考查的重点.在本题的解题过程中，可以综合利用三种解题方法［2］.

对于选项A，可以直接利用定理：

因为PA⊥平面ABCDEF，所以PB在平面ABCDEF内射影为AB.

若PB⊥AD，则AB⊥AD，（三垂线定理的逆定理）

而AB不垂直AD，故选项A不正确.

直接应用定理解题是一种较为直观的、常用的解题方法.

对于选项B和C，可以利用反证法：若平面PAB⊥平面PBC，作AG⊥PB于G，则AG⊥平面PBC，所以BC⊥AG，又BC⊥PA，所以BC⊥平面PAB，所以BC⊥AB，而BC与AB不垂直，所以选项B不正确.

若直线BC∥平面PAE，注意到BC∥AD，而AD与平面PAE相交，所以BC与面PAE相交，故选项C不正确.

反证法同样是一种较为常见的解题方法，尤其是在选择题的解答中，合理利用反证法能够有效提升解题的效率.

对于选项D，可以利用定义法：PD与平面ABC所成角为∠PDA，在Rt△PDA中，因为AD=2AB=PA，所以∠PDA=45°.

定义法在立体几何的解题应用中，具有简单明了、速度较快的特点，但对于一些复杂的题型，定义法解题就显得有些难度.

2.立体几何解答题的解题技巧

例2（2015年湖北卷）在四棱锥O-ABCD中，底面ABCD是边长为1的菱形，∠ABC=，OA⊥平面ABCD，OA=2，M为OA的中点，N为BC的中点.证明：直线MN∥平面OCD.

分析：在线面平行的证明中，通常有多种不同的证明方式，一般较为常用的方法有两种：

证法1：判定定理直接应用法.

如图2，取OD中点E，连接ME，EC，易知ME∥NC.

所以四边形MNCE是平行四边形，

则MN∥EC.

又MN⊄面OCD，EC⊂平面OCD，

所以MN∥平面OCD.

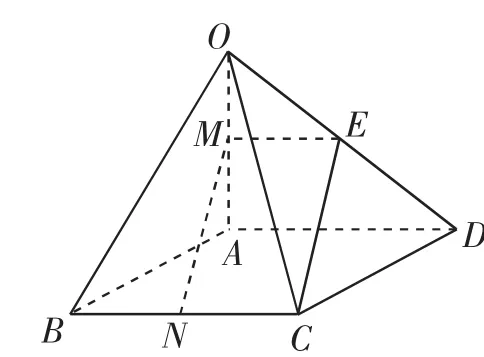
图2

图3

证法2：可以采用面面平行的性质定理，但不容易思考到.［3］

如图3，取OB中点E，易知ME∥CD，又EN∥OC，可分别证得ME∥平面OCD，EN∥平面OCD.

所以平面MNE∥平面OCD.

因为MN⊂平面MNE，所以MN∥平面OCD.

三、结语

高中立体几何的解题技巧可谓是千变万化.但是万变不离其宗，要以不变应万变：点线面体心中留，转化思想少不了，若要解题解得妙，八般武艺才更好.在解题过程中，要时刻谨记转化与降维的思想，同时眼观六路耳听八方，不能总是局限于一种解题的方案上，应当尝试综合运用多种解题方式，从而做到枯藤老树发新枝，柳暗花明又一村.

1.张娜.立体模型在高中立体几何教学中的运用探究［J］.课程教育研究，2017（18）.

2.杜瑞姣.高中立体几何高考试题分析及教学对策研究［D］.洛阳师范学院，2016.

3.佟丽丽.高中立体几何教学的研究［D］.内蒙古师范大学，2015.