圆锥曲线切线的几何画法与证明
☉湖北省阳新县第一中学 石裕望
在做圆锥曲线的习题时,经常会涉及圆锥曲线的切线,需要在图上画出圆锥曲线的切线,但高中数学教材和课外辅导材料都没有提供其画法.本人为此进行了探索,研究并总结出了两种只用直尺、三角尺等常规画线工具就可以准确地画出圆锥曲线上某一点的切线的几何画法,现以命题的形式介绍如下.
一、对称点法
所谓对称点法,就是利用圆锥曲线上已知点的轴对称点和圆锥曲线的顶点,画出圆锥曲线上已知点的切线的方法.
(一)椭圆的切线
命题1 如图1所示,点P是椭圆上的一点,点A,B是椭圆长轴上的两个顶点,过点P作长轴线的垂线交椭圆于点Q(即点P关于长轴的对称点),再作直线AP,QB,设它们交于点M,再过点M作长轴线的垂线交长轴线于点N,则直线PN是椭圆上点P的切线.

图1
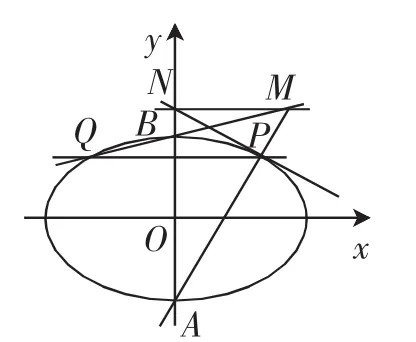
图2
另外,还可知点Q坐标为(x0,-y0),点A坐标为(-a,0),点B坐标为(a,0),
直线AP、QB的交点M满足如下方程组:

所以直线PN就是椭圆上过点P的切线.
以上是利用长轴作画.经进一步研究发现,也可以利用短轴作画,其方法是一样的,即有:
命题2 如图2所示,点P是椭圆上的一点,点A,B是椭圆短轴上的两个顶点,过点P作短轴线的垂线交椭圆于点Q(即点P的短轴对称点),再作直线AP,QB,设它们交于点M,再过点M作短轴线的垂线交短轴线于点N,则直线PN是椭圆上点P的切线.
命题2的证明方法同命题1.
(二)双曲线的切线
命题3 如图3所示,点P是双曲线上的一点,点A,B是双曲线实轴上的两个顶点,过点P作实轴线的垂线交双曲线于点Q(即点P关于实轴的对称点),再作直线AP,QB,设它们交于点M,再过点M作实轴线的垂线交实轴线于点N,则直线PN是双曲线上点P的切线.
命题3的证明方法与上述的椭圆切线完全相同.

图3
(三)抛物线的切线
命题4 如图4所示,点P是抛物线上的一点,过点P作轴线的垂线交抛物线于点Q(即点P关于轴的对称点)、交轴线于点G,过点P作轴线的平行线l,连接点Q和抛物线顶点O的直线交直线l于点M,再过点M作轴线的垂线交轴线于点N,则直线PN是抛物线上点P的切线.

图4
证明:设抛物线的方程为y2=2px,点P(x0,y0)在抛物线上,则2px,且抛物线上过点P的切线的斜率0(证明略).
另外,还可知点Q坐标为(x0,-y0),△MON≌△QOG,得N点坐标为(-x0,0).
所以直线PN就是抛物线上过点P的切线.
二、中点法
所谓中点法,就是利用某一特定线段的中点,画出圆锥曲线上已知点的切线的方法.
(一)椭圆的切线
命题5 如图5所示,点P是椭圆上的一点,点A,B是椭圆长轴上的两个顶点,过点B作长轴线的垂线交直线AP于点M,点N是线段BM的中点,则直线PN是椭圆上点P的切线.

图5

图6
因为点A坐标为(-a,0),点B坐标为(a,0),不难求得
所以直线PN就是椭圆上过点P的切线.
以上是利用长轴顶点作画.同样,经进一步研究发现,也可以利用短轴顶点作画,其方法是一样的,即有:
命题6 如图6所示,点P是椭圆上的一点,点A,B是椭圆短轴上的两个顶点,过点B作短轴线的垂线交直线AP于点M,点N是线段BM的中点,则直线PN是椭圆上点P的切线.
命题6的证明方法同命题5.
(二)双曲线的切线
命题7 如图7所示,点P是双曲线上的一点,点A,B是双曲线实轴上的两个顶点,过点B作实轴线的垂线交直线AP于点M,点N是线段BM的中点,则直线PN是双曲线上点P的切线.
命题7的证明方法与上述的椭圆切线完全相同.

图7

图8
(三)抛物线的切线
命题8 如图8所示,点P是抛物线上的一点,坐标轴原点O是抛物线的顶点,过点P作轴线的平行线交y轴于点M,点N是线段OM的中点,则直线PN是抛物线上点P的切线.
证明:设抛物线的方程为y2=2px,点P(x0,y0)在抛物线上,则抛物线上过点P的切线的斜率
另外,还可知点M的坐标为(0,y0),N点坐标为
所以直线PN就是抛物线上过点P的切线.
1.相生亚,裘良.圆锥曲线的一类切线的几何画法.数学通报,2004(2).

