城际铁路设站城市选择优化模型
张天伟,赵媛媛,闫绍辉,李 峰
(1.石家庄铁道大学交通运输学院,河北石家庄050043;2.河北建投交通投资有限责任公司投资发展部,河北石家庄050051)
在铁路运输系统中,车站具有十分重要的地位,合理的客运站设置有助于提高交通的可达性[1]。目前,我国城际铁路正在进入规划设计和施工建设高峰期。设站城市选择是城际铁路规划设计时一个重要因素,目前对于车站设计的研究多集中于车站选址[1-3]、车站站型设置[4-5]、车站出站口设置[6]等方面,均是在设站城市已知的情况下根据城市具体情况及旅客需求研究车站在城市中的具体选址和站型设计。关于设站城市选择的研究较少,雒继峰[7]从铁路车站对城市的促进作用、铁路车站与城市交通运输系统关系等方面探讨铁路历经城市设站的合理模式,并对西安市铁路车站设置进行研究,但缺少设站城市选择的量化分析;陈卓[8]、张天伟等[9]主要研究铁路网规划,对于设站城市选择仅提出大城市应该设置车站。为此,研究城际铁路设站城市选择优化问题十分重要。
1 城际铁路设站城市选择问题描述
决定修建城际铁路时,一般已知起点城市和终点城市,再进行选线设计,即根据起点城市与终点城市之间城市的地理位置、人口数量、经济状况、占地面积和交通情况等,规划线路的基本走向,即线路途经哪些城市,在哪些城市设站。假设规划城际铁路起点与终点城市及中间城市相对位置示意图如图1 所示。在图1 中,规划在城市 1 和 13 之间修建城际铁路,则需要确定城际铁路从城市 1 引出后需要引入哪个城市,如果为城市 2,则从城市 2 引出后需要引入哪个城市,依次类推,直至引入城市13,即完成选线设计。对线路设计具有决定性影响的一般是修建难度与修建成本。

图1 规划城际铁路起点与终点城市及中间城市相对位置示意图Fig.1 Locations of the starting city, terminal city and the intermediate cities of the planned intercity railway
选线设计时,如果规划线路没有通过某一城市,则无法在该城市设置车站,即使通过某城市也需要综合考虑线路功能定位、城市自身情况等确定是否在该城市设置车站。但是,城际铁路则有所不同,一般认为,城际铁路主要服务于相邻城市间或城市群,即主要服务于一些中小城市,只要通过该城市一般均设置车站。假设所研究的所有城市均具备设站条件,最终是否设置车站则需要根据优化结果确定。
由图1 可知,城际铁路从城市 1 引入城市 13,有多种走向方案。一般做法是对有可能经过的城市2 至城市 12 的城市规模、预测客货运量等因素进行综合评估,确定城际铁路必须经过的城市 (以下称为“重要城市”) 和不是必须经过的城市 (以下称为“非重要城市”),然后在此基础上采用修建费用最小的方式决定城际铁路走向,即图论中的最小树问题[9](铁路线路一般为线形结构),也就确定了设站城市和修建线路。在进行最终决定时也会综合考虑,有可能减少途经重要城市数量,增加非重要城市数量。
比如对图1 中的城市经过综合评估,认为重要城市为 3,4,5,10,11,12,非重要城市为 2,6,7,8,9。假设利用最小树算法确定的途经所有重要城市城际铁路走向示意图如图2 所示,即在城市 1 和 3、3 和 5、5 和 4、4 和 10、5 和 7、7 和 11、11 和 12、12 和 13 之间修建城际铁路,在城市 1,3,4,5,7,10,11,12,13 设置车站。图2 中包含非重要城市 7,主要是其与重要城市 5 和 11 基本在一条直线上,通过该城市并不显著增加线路修建费用。
图2 中城际铁路走向不是线形结构,而是树形结构,树形结构与线形结构相比,将增加后期列车运营及调度指挥的难度。此时进行调整时可以有以下 2 种方案,一种是在所有重要城市之间寻找费用最小的线形结构,如图3 所示。一种是不通过重要城市 4 和 10,结果如图4 所示。在图3 中,城市 3和 11、5 和 11 之间的实际距离较理论最短路相差很大,产生了很高的绕道率。在图4 中,尽管不产生很高绕道率,但缺少了重要城市 4 和 10。由此可以看出,由图2、图3 和图4 得到的方案都各有优缺点。
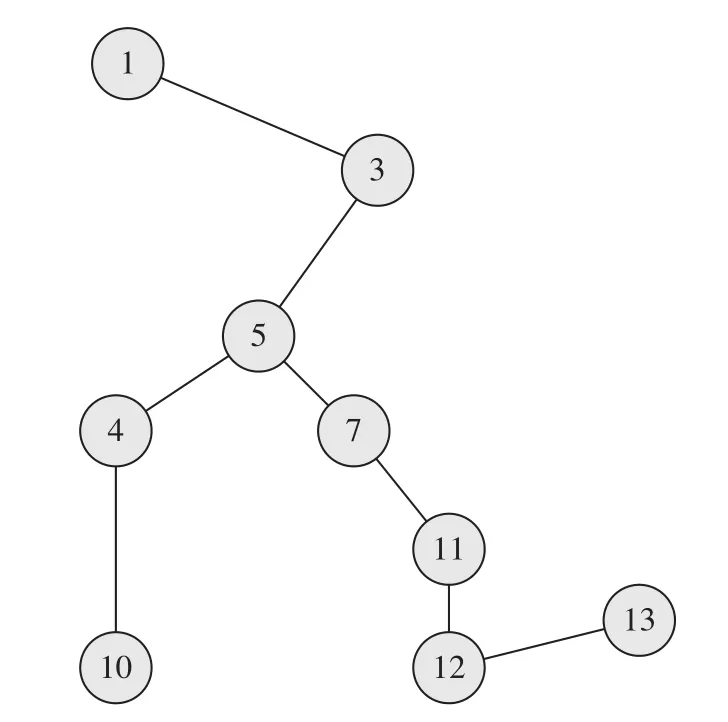
图2 利用最小树算法确定的途经所有重要城市城际铁路走向示意图Fig.2 Route of the intercity railway with all the important cities selected using the minimum tree algorithm
城际铁路车站设站城市合理方案应是在所有建设费用最小的情况下保证车站覆盖所有城市,且绕道率不宜过高。其中,车站覆盖所有城市并非在所有城市设置车站,而是在一个城市设站可以覆盖周边城市。这种情况不同于图论中的最小树问题,也不同于图论中的最短路问题。因为最小树需要确定设站城市,研究认为合理方案中设站城市为变量,且经由最小树求解的线路走向有可能不是线形结构,并有可能产生较高的绕道率。最短路不能保证车站覆盖率,有可能造成部分城市居民无法实现经由铁路出行。接下来将对城际铁路设站城市方案进行优化,假定城际铁路为线形结构,并且对于城市不区分重要城市和非重要城市。

图3 途经所有重要城市的线形结构城际铁路设站示意图Fig.3 Linear structure of inter-city railway stations in all important cities

图4 途经部分重要城市的线形结构城际铁路走向示意图Fig.4 Linear structure of inter-city railway stations in some important cities
2 城际铁路设站城市选择模型构建
2.1 参数及变量定义
M为确定具备修建城际铁路车站城市的个数,对所有城市按 1,2,…,M的自然序列进行编号,其中编号为 1 和M的城市分别为城际铁路的起点城市和终点城市。Ci为在城市i(i= 1,2,…,M) 修建城际铁路车站的工程费用,亿元;Cij为城市i和城市j之间修建城际铁路的工程费用,亿元;为方便计算,认为当i=j时,Cij= 0,并且存在Cij=Cji;F(i) 为如果要覆盖城市i需要设站城市的集合;Lij为城市i和城市j之间修建城际铁路的最短距离,km,为方便计算,认为当i=j时,Lij= 0;xi为 0-1变量,当在城市i设置城际铁路车站时为 1,否则为 0,由此可知x1=xM= 1,即城际铁路起点城市和终点城市一定设置车站;yij为 0-1 变量,在城市i和城市j之间修建城际铁路时为 1,否则为 0,为方便计算,认为当i=j时,yij= 0。
2.2 优化模型
(1)目标函数。根据前文可知,目标函数为修建城际铁路及城际铁路车站工程的总费用最低,即
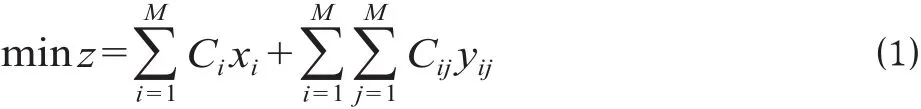
式中:z为修建城际铁路及城际铁路车站工程的总费用为修建城际铁路车站的工程费用,为在城市之间修建城际铁路的工程费用,用,具体费用大小与模型求解结果有关。
(2)变量逻辑约束。模型中 2 组决策变量xi与yij存在逻辑关系约束,具体为
(4)绕道率约束。为避免起点城市与终点城市城际铁路的实际距离与最短距离相差过大,采用以下约束。
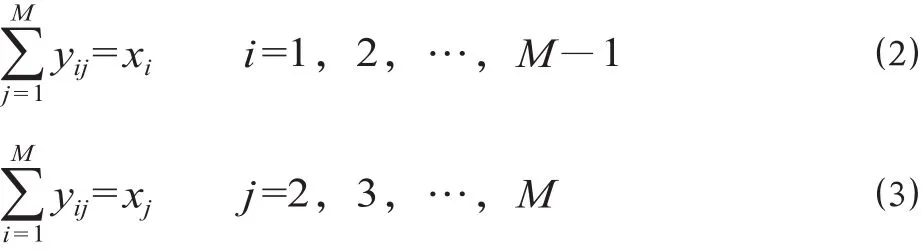
公式 ⑵ 表示,在城市i是否设置城际铁路车站与是否在该城市与其他城市之间修建城际铁路存在逻辑关系,如果在城市i设置城际铁路车站,则xi= 1,则一定要从城市i引出城际铁路,如果xi= 0,则一定不会从城市i引出城际铁路,该城市取值范围为编号从 1 到M-1,即终点城市不引出城际铁路;公式 ⑶ 表示,在城市j是否设置城际铁路车站与是否在其他城市与该城市之间修建城际铁路存在逻辑关系,如果在城市j设置城际铁路车站,则xj= 1,则一定要有城际铁路引入城市j,如果xj= 0,则一定不会有城际铁路引入城市j,该城市取值范围为编号从 2 到M,即起点城市不引入城际铁路。公式 ⑵ 和公式 ⑶ 保证城际铁路走向为线形结构。
在模型求解时,出于目标函数的考虑,有可能出现yij=yji= 1 的情况,即从城市i引出的城际铁路引入了城市j,从城市j引出的城际铁路引入了城市i,在城市i和j之间形成一个死循环,无法到达终点城市。为避免此种情况发生,引入公式 ⑷如下。

公式 ⑷ 表示任意 2 个城市之间最多修建 1 条城际铁路,即不存在yij=yji= 1 时描述的死循环,该约束不应该通过yij≠yji实现,因为两城市之间不修建城际铁路时,无法满足该约束。
(3)车站覆盖约束。为保证所有城市居民均可以通过车站乘坐城际铁路列车,则所选择的设站城市必须覆盖所有城市,即

公式 ⑸ 表示如果要覆盖除起点城市和终点城市之外所有城市,则必须在可以覆盖其的城市中至少有一个城市设置车站。

式中:α为能够接受的最大绕道率,α≥1;L1,M为起点城市与终点城市修建城际铁路的最短距离,km。
需要说明的是,在α一定的情况下,公式 ⑸ 和公式 ⑹ 共同约束有可能出现模型无解的情况,此时一般要将α值继续增加或直接取消该约束,一般城际铁路起点城市和终点城市之间修建有高速铁路,2 个城市之间的客流可以经由高速铁路实现出行。
(5)已知变量约束。优化模型中部分变量已知,例如x1=xM= 1,yij= 0 (i=j时),即起点城市和终点城市必须修建城际铁路车站,同一城市之间无需修建城际铁路。
综上所述,城际铁路设站城市选择优化模型如下。

3 算例应用
以图1 为算例验证模型的有效性和准确性,为求解方便,不再考虑公式 ⑹ 表示的约束。其他已知条件为:M = 13,F (2) ={1,2},F (3) ={3,6},F (4) ={4,5,8},F (5) ={4,5,7,8},F (6) ={3,6},F (7) ={5,7,8},F (8) ={5,7,8,9},F (9) ={8,9,10},F (10) ={8,9,10},F (11) ={7,11,12,13},F (12) ={11,12,13}。
Ci= [5.2 3.4 2.8 2.8 4.8 3.2 2.9 4.6 3.9 3.7 5.8 4.3 6.8]

利用软件 lingo 11.0 求解,不足 1 s 得出最优解,具体决策变量结果为:x1= 1,x3= 1,x7= 1,x8= 1,x11= 1,x13= 1,y1,3= 1,y3,7= 1,y7,8= 1,y8,11= 1,y11,13= 1,其余决策变量结果为 0,最优值176.1 亿元。如果不考虑车站覆盖约束,求解结果为:x1= 1,x3= 1,x6= 1,x13= 1,y1,3= 1,y3,6= 1,y6,13= 1,其余变量结果为 0,最优值为 140 亿元。上述 2 种求解结果的城际铁路走向图如图5 所示。
由图5 可知,在不考虑车站覆盖约束和绕道率约束的前提下,需要设置车站的城市为 1,3,6,13,与图论中最短路求解结果相同,此时修建城际铁路及车站费用之和最小为 140 亿元,但多数城市居民无法享受城际铁路带来的便利。考虑车站覆盖约束后,求解结果发生变化,需要设置车站的城市为 1,3,7,8,11,13,总费用最小为 176.1 亿元,其中在城市 8 修建车站可以覆盖城市 4,5,8,9,10,因为城市 3 和城市 8 之间无法直接修建城际铁路,只有通过城市 7。
如果将城市 3 与 6 之间城际铁路的修建费用提高到 100,在不考虑车站覆盖约束的前提下,利用本模型借助 lingo 11.0 在 1 s 内实现求解,根据求解结果可知需要设置车站的城市为 1,5,7,11,13,总费用为 144.5 亿元。可见,所构建的模型对于求解此类问题具有准确性和有效性。

图5 2 种模型求解结果的城际铁路走向图Fig.5 Inter-city railway stations course planning with two results of model solving
4 结束语
我国城际铁路已经进入规划设计和施工建设的高峰期,而设站城市选择是城际铁路规划设计时的重要因素之一。首先利用图论中的最小树原理给出设站城市选择的多种方案,并且对不同设站方案从铁路建设成本、城市覆盖情况、线路绕道率、列车运营组织难度等方面进行定性评价,对设站城市选择问题进行描述,然后对设站城市选择构建以修建城际铁路及城际铁路车站工程的总费用最低为优化目标的 0-1 规划模型,最后设计算例应用模型,通过相关参数的变化及其求解结果,验证了模型的有效性和准确性,对城际铁路设站城市选择具有参考价值。
[1] 李 松,刘力军,白 洋. 铁路车站站点设置对县域交通可达性的影响分析[J]. 铁道运输与经济,2017,39(7):77-82.LI Song,LIU Li-jun,BAI Yang. Analysis on Influence of Railway Stations Setting on County-level Traf fi c Accessibility[J].Railway Transport and Economy,2017,39(7):77-82.
[2] 朱晓宁,席江月. 基于熵权-TOPSIS 的城际铁路客运站选址研究[J]. 铁道运输与经济,2013,35(10):32-36.ZHU Xiao-ning,XI Jiang-yue. Study on Location of Intercity Railway Passenger Station based on Entropy Weighting-TOPSIS[J]. Railway Transport and Economy,2013,35(10):32-36.
[3] 张天伟,聂 磊,高桂凤. 铁路客运站选址模型[J]. 交通运输工程学报,2011,11(5): 83-87,92.ZHAO Tian-wei,NIE Lei,GAO Gui-feng. Location Model of Railway Passenger Station[J]. Journal of Traffic and Transportation Engineering,2011,11(5):83-87,92.
[4] 杨 宇,陈 刚,郑才辉. 城际铁路新建客运站研究[J].铁道工程学报,2007(10):65-68.YANG Yu,CHEN Gang,ZHENG Cai-hui. Research on the Newly-built Passenger Station of Intercity Railway[J].Journal of Railway Engineering Society,2007(10):65-68.
[5] 杨 宇,陈 刚,袁光明. 城际铁路车站设置模式研究[J].铁道运输与经济,2007,29(9):11-14.YANG Yu,CHEN Gang,YUAN Guang-ming. Research on Establishment Mode of Intercity Railway Station[J]. Railway Transport and Economy,2007,29(9):11-14.
[6] XU Xiao-ling,MA Li-li,GUO Da-gang,et al. Discussion on Design of Egress in Underground Inter-city Railway (UIR)Station in China[J]. Procedia Engineering,2014(71):7-15.
[7] 雒继峰. 铁路历经城市设站的一般模式分析[D]. 西安:长安大学,2005.LUO Ji-feng. The General Pattern Analysis of the Railroad Crossing through the City Sets up a Station[D]. Xi’an:Chang’an University,2005.
[8] 陈 卓. 城际铁路规划方案研究[J]. 铁道运输与经济,2013,35(3):35-39.CHEN Zhuo. Research on Inter-city Railway Programming[J].Railway Transport and Economy,2013,35(3):35-39.
[9] 张天伟,颜月霞. 铁路网规划的图示法[J]. 铁道运输与经济,2007,29(1):87-89.ZHANG Tian-wei,YAN Yue-xia. Graphic Presentation of Railway Network Planning[J]. Railway Transport and Economy,2007,29(1):87-89.

