基于双层规划模型的京沪高速铁路票价研究

雷 蕾，朱加发，周 茵，王怀相

（1.中国铁道科学研究院研究生部，北京 100081；2.中国铁道科学研究院运输及经济研究所，北京100081）

0 引言

随着铁路市场化改革进程的推进，高速动车组列车实行市场化定价成为必然趋势。自 2016 年 1 月1 日起高速铁路动车组列车票价放松管制以来，除新建客运专线实行新运价外，中国铁路总公司对已经开通的海南环岛高速铁路及东南沿海高速铁路动车组列车票价进行了调整，但总体票价改革较为缓慢。2017 年 4月，中国铁路总公司下发的《中国铁路总公司关于建设京沪高铁标准示范线的指导意见》提出：有序推进京沪高速铁路标准示范线建设，努力创建世界一流水平高速铁路。京沪高速铁路应充分利用国家对高速铁路票价管理的新政策，加强市场化定价理论研究，建立市场化票价体系，有利于提升高速铁路竞争力、增加铁路运营效益，为高速铁路票价市场化提供研究支撑。

目前我国学者对铁路定价方法的研究多数从运输企业角度出发，以提高企业盈利水平为目标，其中双层规划模型在旅客运输定价方面的理论研究取得一定成效。四兵锋等[1]建立了以运输企业利润最大化和旅客广义出行费用最小化为上下层的双层规划模型，通过启发式灵敏度分析法求解，并辅以算例验证了模型的有效性。陈建华等[2]为解决不同速度等级普通旅客列车及其他交通运输方式的竞争对客运专线的影响，构建了具有弹性需求特点的双层规划模型并对其进行求解。刘玉敬[3]通过测算运输市场细分条件下的不同旅客广义出行费用，构建了基于旅客出行选择行为的高速铁路客票定价模型，并验证了模型的有效性和合理性。刘立荣[4]通过对传统客票定价方法的优劣进行分析，结合旅客时间价值因素构建定价模型，以京津城际铁路、武广客运专线、京沪高速铁路为例进行实证研究。程谦[5]运用双层规划模型优化城际动车组列车客票价格，对沪宁城际铁路日收益率进行了计算。袁任[6]基于不同停靠站方案、旅客到达率和客票销售规则等因素，以企业收益最大化为上层、Logit 模型选择客流分配为中层和客票销售规则流程为下层建立三层规划优化模型，进行模型求解的同时检验算法的收敛性及稳定性。姜达[7]从不同运输方式旅客票价、客运收入和客运量的角度出发，建立双层规划票价优化模型，并采用改进粒子群的双层迭代算法对模型进行求解。为此，基于市场环境下不同运输方式之间的竞争，采用双层规划模型对京沪高速铁路市场化定价进行实证分析，并提出相关发展建议。

1 高速铁路旅客票价制定双层规划模型的建立

双层规划模型考虑了上下层决策者在追求利益过程中的作用及表现，并依据对方的反应而做出决策。其中，运输企业为上层决策者，旅客为下层决策者。运输企业可以通过政策或管理改变服务和运输成本来影响旅客的出行选择行为，基于运输企业和旅客 2 个方面分析，采用双层规划模型对旅客票价制定过程进行描述，得出运输企业在供需均衡状态的最优票价。

1.1 模型构建

双层规划模型包含上、下 2 层规划模型，其中上层问题是以下层问题为约束条件的规划问题。针对运输定价问题，上层规划模型可以描述为不同运输方式的企业运营效益最大化，下层规划模型可以描述为不同运输方式均衡配流状态下的旅客广义出行费用最小化。其中，以运输企业效益最大化为目标函数的上层规划模型[8]为

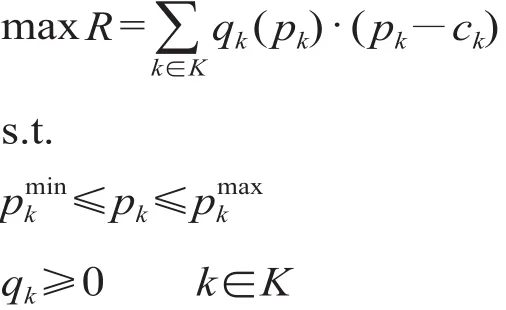
式中：R为各种运输方式的运营总利润；qk为第k种运输方式的客运量；pk为第k种运输方式的票价；ck为第k种运输方式的单位旅客运输成本；pkmin，pkmax分别为旅客运输的平均单位运输成本和最高限价；k为旅客运输方式；K为不同交通运输方式的集合。

旅客在实际出行过程中，总是愿意选择广义费用最小的出行方式，最终达到用户均衡状态[9-10]，则基于旅客选择行为的下层规划模型为

式中：Z为 OD 间不同运输方式下的旅客广义出行费用之和；f(x) 为 OD 间第k种运输方式的广义费用函数；Qk为 OD 间不同运输方式的总客运量。

采用对数函数形式描述广义费用函数[11]

式中：Vk第k种交通运输方式能够观测到的效用值。

影响旅客出行方式选择的因素较多，主要有经济性、快速性、便捷性、舒适性、安全性、准时性及个人偏好等。由于准时性和个人偏好等因素对效用值影响较小，而且难以量化，因而主要考虑前 5个因素对广义费用的影响。经济性费用为旅客出发和达到城市市内衔接交通工具，以及 OD 间所选交通方式的费用之和；快速性费用为旅客乘坐第k种交通工具过程中所花费的时间乘以旅客的平均单位时间价值；便捷性费用主要考虑旅客在选择某种运输方式过程中乘坐市内衔接交通工具时间、购票时间、车站排队等待时间、不同交通运输方式之间的中转时间及列车开行密度等因素；舒适性费用表现为不同运输方式旅客恢复疲劳所需时间与旅客时间价值的乘积；安全性效用为影响效用函数整体的因素，采用乘法原则表示，当安全性与其他服务属性同时较优时，总体效用才表现最优。不同运输方式的可观测费用是效用函数值的相反数。

因此，建立的可观测费用函数形式为

式中：ω1，ω2，ω3，ω4分别经济性、快速性、便捷性和舒适性的权重系数；Pk，Fk，Tk，Ak和Sk分别表示经济性费用、快速性费用、便捷性费用、舒适性费用和安全性效用。

OD 间的客运需求量受城市发展水平、人口规模、居民收入水平等因素影响，通常采用的需求函数形式如下。

式中：Qmax为 OD 间客运需求总量；AO，BD是 OD点两端节点的相关参数；h(μ) 是关于旅客出行费用μ的单调递减函数。

1.2 模型转化

上层规划模型考虑了不同运输方式客运市场需求的分担模式，可以用来解决 OD 间不同运输方式单一运营企业客运产品的定价问题，因而客运市场中第k种运输方式下运输企业总的利润为

式中：Rk为 OD 间第k种运输方式的运营总利润。

旅客出行需求总量总是随着广义费用的变化而变化，但其大小受各种运输方式运输能力的限制，考虑该需求弹性问题，则下层规划模型可以转化为具有能力约束的需求弹性模型。

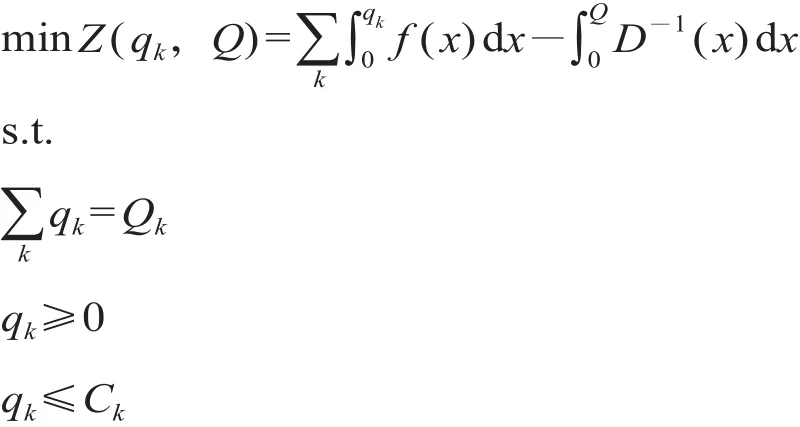
式中：D-1(x) 为需求函数的反函数；Ck为第k种交通运输方式的运输能力。

通过引入超量需求法，将原弹性需求问题转换为固定需求问题[12]。假设Qmax表示参与市场竞争的各种运输方式的运输能力之和，空余能力e可以表示为

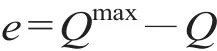
通过定积分换元法[13]可以将下层旅客选择目标函数转换为

扩展反函数D-1(Q)，建立超量变量e的广义费用函数R(e)

结合扩展函数，目标函数最终改进为

假设在 OD 点之间增设一条虚拟运输方式，且客流量为e，则参与竞争的运输方式由K种增加为K+ 1 种，当各种运输方式之间的客流量达到均衡状态时，其目标函数可以表示为

通过对上述模型进行求解，即可获得在既定决策目标下的高速铁路最优票价。

2 高速铁路旅客票价制定双层规划模型求解

利用灵敏度分析法求解双层规划模型，将下层决策变量对上层决策变量的反应函数q(p) 进行简化，对不同交通运输方式客运量与旅客票价进行求导，并通过泰勒展开式对反应函数进行线性近似，进而求解双层规划模型。

首先将双层规划下层模型中的用户均衡配流问题通过变分不等式[12]表示。

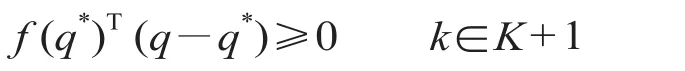
式中：q∈ {q|Q=HTq，q≥0}；HT为关联矩阵；q*表示下层规划模型的均衡解。

将旅客票价p作为变分不等式的扰动项，同时其他影响因素如快速性、舒适度、便捷性等均保持不变。q*(p) 为p的函数，将其转化为

式中：所有q∈ (q(p) |Q=HTq(p)，q(p)≥0)。

如果变分不等式在p=p(0)时有唯一解，此时引入拉格朗日乘子向量μ，则p=p(0)时的必要条件为

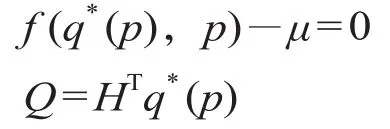
令y(p) = [q*(p)，μ(p)]T，用Jy(p) 表示对于p的雅各比矩阵，则有

假设p*1(0)为 OD 对间铁路旅客票价的初始值，且其他交通运输方式的票价为固定不变，即可以通过对下层模型求解得到 OD 对间铁路旅客运量q*1(0)(p*1(0))，并求出铁路客运量对票价的偏导数∂q1/ ∂p1，通过泰勒展开式即可得到反应函数q(p) 的线性近似形式。

将其代入上层规划模型，则上层问题转化成为非线性优化问题，上层问题的最优解即最优票价。

模型求解具体步骤如下[14]。

步骤 1：初始化。确定各运输方式的初始票价{pk(0)|k∈K+ 1}、广义费用函数相关参数、虚拟运输方式的反需求函数形式、平均客运成本和需求上限Qmax等，并记迭代次数j= 0，设定迭代精度ε*。

步骤 2：在 {pk(j)|k∈K+ 1} 的条件下 (虚拟运输方式无需定价)，求解下层规划模型，得到客运量分配方案 {|k∈K+ 1}，包括用户均衡配流模型的均衡解{}。

步骤 3：用灵敏度分析法求出第k种运输方式的客运量对扰动参数 (铁路客运价格) 的导数 ∂qk/ ∂pk(k∈K+ 1)，求出反应函数的线性近似表达式。

步骤 4：将反应函数代入上层规划模型，采用非线性优化求解算法得到新的铁路客运价格{p1(j+1)|k∈K+ 1}，求解时需避免所求解为上层目标函数的局部最优解。

步骤 5：收敛判断。若 |p1(j+1)-p1(j)|≤ε*，满足迭代精度要求，则算法停止；否则令j=j+ 1，返回步骤 2 继续迭代，直至满足迭代精度要求。

3 实例分析

以京沪高速铁路 (北京南—上海虹桥) 为例，通过双层规划模型对市场竞争条件下的高速铁路票价制定过程进行探讨，对其二等座执行票价水平进行测算。考虑该 OD 间主要存在高速铁路、普通旅客列车、民航 3 种运输方式的竞争，各运输方式的旅客广义费用函数形式f(qk) 为

式中：k= 1，2，3，分别代表高速铁路、普通旅客列车和民航 3 种运输方式；β为待定参数，Vk为第k种交通运输方式的效用函数。

假设 OD 间总运输需求量上限已知且为固定值，且普通旅客列车和民航票价水平及服务属性不变，各种交通运输方式的属性参数如表1 所示。

表1 各种交通运输方式的属性参数Tab.1 Attributes parameters for different transport modes

其中，p1为高速铁路单位里程运价率，其范围为 0.308 6～0.73 元/人公里，0.308 6 元/人公里为速度 200 km/h 动车组列车二等座公布票价率，0.73元/人公里取全路高速铁路最高运价率，即广深铁路单位里程运价率；以无空调普通旅客列车硬座票价率 0.058 61 元/人公里为基准，北京至上海特快空调列车硬座票价水平为 177.5 元；民航票价为中国国际航空公司、中国东方航空公司和中国南方航空公司三大航空公司北京至上海 2017 年 11 月经济舱最低平均票价 645.25 元 (含国内航线机场建设费 50元)；北京至上海高速铁路、普通旅客列车及民航平均花费时间分别为 5.52 h、15.13 h、2.29 h；高速铁路、普通旅客列车和民航两端中转时间分别取 1.4 h、1.0 h、2.4 h；时间价值取 2016 年北京和上海职工平均工资 42.46 元/h；同时进行舒适性费用计算[15]。

OD 对之间的广义费用权重系数如表2 所示。

表2 OD 对之间的广义费用权重系数Tab.2 Generalized cost weighting coefficients between OD pairs

假设D-1(Qk) = 1 000-0.1Qk，Qmax= 10 000 人/次，得到虚拟运输方式的阻抗函数f4(q4) = 0.1q4，灵敏度分析的迭代精度ε*= 0.000 1。利用 Matlab2015b软件中的非线性优化求解函数对双层规划模型进行求解，将高速铁路票价的初始值分别设为 0.5，0.6和 0.7，虽然迭代次数不同，但最优解都为 0.483 8元/人公里。

通过求解双层模型，得出北京至上海高速铁路二等座单位里程运价率最优为 0.483 8 元/人公里，此时票价为 637.7 元，高速铁路市场分担比例为51.42%。考虑到铁路现场实际售票过程实际，对模型结果取整为 640 元。北京至上海高速铁路二等座640 元票价与现行票价水平相比，涨幅达到 15.7%，结合北京及上海职工 2016 年工资水平及运输市场竞争环境，高速铁路的票价在合理范围内。

4 结束语

基于运输企业利润最大、旅客广义费用最小为目标，建立考虑旅客均衡配流的双层规划模型，利用灵敏度分析法对模型进行求解，并以北京至上海高速铁路二等座票价为例进行测算，得出最优票价。对于高速铁路，一是应优化票价结构，构建多级票价体系，调整当前单一化的票价水平结构，构建基于服务质量、列车速度等级、运营时段、市场竞争等因素的差异化票价体系，依据市场变化及时调整高速铁路执行票价水平，以实现利益最大化，引导运输市场合理分工、优化资源配置，实现企业健康可持续发展；二是丰富票种形式，实行票价优惠策略，基于有效的运输市场细分，构建旅客出行数据库，建立与旅客相关的票价优惠形式，实行常旅客优惠、预订车票优惠、空铁/地铁联程优惠等丰富多变的票价策略，以满足不同层次人群出行服务需求。

[1] 四兵锋，高自友. 多模式交通条件下合理制定旅客票价的优化模型及算法[J]. 中国管理科学，2000，8 (4)：56-63.SI Bing-feng，GAO Zi-you. Optimal Model and Solution Algorithm for Passenger-Ticket Pricing under the Condition of Multimodal Transportation[J]. Chinese Journal of Management Science，2000，8(4) ：56-63.

[2] 陈建华，高自友. 多模式条件下需求变动时铁路客票价格制定的优化模型及算法[J]. 交通运输系统工程与信息，2001(4)：299-305，330.CHEN Jian-hua，GAO Zi-you. A Bi-level Model and Solution Algorithm for Passenger-Ticket Pricing Problem under the Condition of Multi-model Transportation with Elastic Demands[J]. Journal of Communication and Transportation Systems Engineering and Information，2001(4)：299-305，330.

[3] 刘玉敬. 基于旅客出行选择行为的高铁客票定价方法研究[D]. 北京：北京交通大学，2015.

[4] 刘立荣. 基于旅客时间价值的客运专线客票定价理论与实证研究[D]. 北京：北京交通大学，2010.

[5] 程 谦. 双层规划模型在沪宁城际铁路客票价格优化中的应用[J]. 现代交通技术，2015，12(2)：77-80.CHENG Qian. Research on Bi-level Programming Model for Ticket Price Optimization for Shanghai-Nanjing Intercity Railway[J]. Modern Transportation Technology，2015，12(2)：77-80.

[6] 袁 任. 客运专线收益管理理论与方法研究[D]. 长沙：中南大学，2011.

[7] 姜 达. 基于不同交通运输方式竞争的高速铁路票价制定方法研究[D]. 成都：西南交通大学，2014.

[8] 胡长英. 双层规划理论及其在管理中的应用[M]. 北京：知识产权出版社，2012.

[9] MEYER M D，MILLER E J. Urban Transportation Planning：A Decision Oriented Approach[M]. New York：Mcgraw-Hill Book Company，2001.

[10] WARDROP J G. Some Theoretical Aspects of Road Traffic Research[J]. Proceedings of The Institution of Civil Engineers，1952，1(5)：325-362.

[11] 高自友，四兵锋. 市场竞争条件下铁路旅客票价制定的模型与算法[J]. 交通运输系统工程与信息，2001，1(1)：50-55.GAO Zi-you，SI Bing-feng. Optimal Model and Solution Algorithm for Railway Passenger-fare Pricing in the Market Competition[J]. Journal of Communication and Transportation Systems Engineering and Information，2001，1(1)：50-55.

[12] 陈建华. 铁路旅客票价优化问题的相关模型及算法[D]. 北京：北京交通大学，2007.

[13] 郎艳怀. 非对称信息和弹性需求下的供应链激励机制研究[J]. 中国管理科学，2012，20(5)：106-111.LANG Yan-huai. Incentive Mechanism in Supply Chain under Asymmetric Information and Elastic Demand[J]. Chinese Journal of Management Science，2012，20(5)：106-111.

[14] 邱 奇，唐永忠，王 皓. 基于双层规划模型的京津冀城际铁路票价水平研究[J]. 铁道运输与经济，2017，39(8)：1-5.QIU Qi，TANG Yong-zhong，WANG Hao. Study on Beijing-Tianjin-Hebei Inter-city Railway Fare Level based on Bi-level Programming Model[J]. Railway Transport and Economy，2017，39(8)：1-5.

[15] 张铱莹，彭其渊. 客运专线对运输通道分担率的影响[J].铁道运输与经济，2006，28(12)：16-19.ZHANG Yi-ying，PENG Qi-yuan. Effect of Passenger Dedicated Lines on the Sharing Rate of Transportation Corridors[J]. Railway Transport and Economy，2006，28(12)：16-19.