基于安全风险的铁路自备车运输路径选择研究

霍明坤，郎茂祥，李晓海，张秀娜，于 潇

（1.北京交通大学交通运输学院，北京100044；2.中国铁路总公司货运管理处，北京100844；3.中国铁路信息技术中心中铁信弘远公司，北京100038；4.中国铁道科学研究院通信信号研究所，北京100081）

0 引言

铁路自备车是指企业出资购置的经国家铁路过轨运输的铁路车辆，是铁路运输的重要组成部分和运输产品的必要补充，其运输过程从向铁路部门提报要约开始，签订过轨运输协议并在企业专用线进行装卸车作业，在上报运输计划得到批复后方可进入国家铁路运行。铁路自备车在路径安排上与普通货车一致，均服从铁路调度人员统一指挥，但由于其承运危险货物较多，通过人口密集区域及客运较繁忙线路时的潜在风险较大，因而为保证运输安全，有效降低潜在风险，铁路自备车应选择一条兼顾效益与安全的运输路径。

在运输路径选择方面，陈钢铁等[1]针对某一特定源点和目的地间的车辆运输调度问题，建立基于成本和时变条件的路径优化模型，并用改进蚁群算法求解。陈文强等[2]设计了考虑运输过程和换乘过程时间延迟的最小费用路径模型及算法。Yan 等[3]建立了环境风险约束下的危化品多式联运路径选择模型，并设计了启发式算法求解。陈浩等[4]以超限运输的装载方案和运输路径优化为主要目标，以装载方案符合基本要求、路段运输限界、线路通过能力为约束，构建了综合优化模型并设计遗传-蚁群算法进行求解。在运输风险管理方面，崔发生[5]分析研判专用线货运安全风险，对全过程控制专用线货物运输安全风险提出具体举措。Madala[6]对多起讫点对的高风险运输问题进行风险模拟分析，并评估事故发生后需疏散的人口数。既有研究偏重于风险评估与管理的定性分析与评价，缺少相对定量的风险量化指标与方法，并且运输径路选择多以公路运输为背景。为此，在既有研究的基础上，考虑运输路线上旅客运输及线路周边人员可能承受的风险，建立以运输过程费用与风险最小化为目标的路径选择 0-1 整数规划模型，并设计自备车路径选择实例，用 Lingo 软件进行求解，比较分析不同风险权重下的运输路径差异。

1 铁路自备车运输路径选择模型

1.1 问题描述

铁路自备车运输路径选择问题是指利用企业自备车从运输任务的起点和终点之间存在的一系列可供选择的路径中选取合理的运输路线。为便于建模求解，简化实际问题，构建以城市为发送、中转、到达节点，以铁路线路为弧段的抽象网络如图1 所示。记I为节点集合，i，j为节点，i，j∈I；T为需求 OD 集合，k为货运需求，网络上存在k个需求OD，k∈T；Ok和Dk分别为需求k的起始节点和终止节点；A为弧段集合，(i，j) 表示起点为i节点，终点为j节点的弧段，(i，j) ∈A。设定以下假设：①同一 OD 的货物在运输过程中不可拆分；②若相邻节点间存在多条铁路，则默认选择距离最短的一条。

图1 抽象网络图Fig.1 Abstract network

1.2 模型构建

以铁路自备车运输费用最小、运输线路上旅客的潜在风险最小、运输线路周边的人员安全风险最低为目标，构建铁路自备车运输路径选择模型如下。

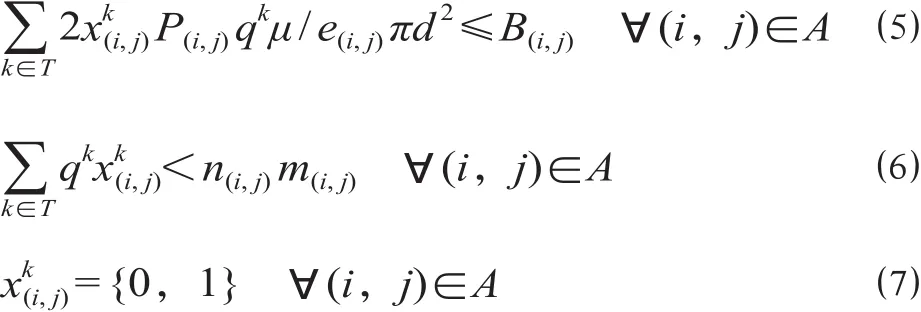
式中：Z1'为运输费用最小值，元；Z2'为运输线路上旅客的潜在风险最小值；Z3'为运输线路周边的人员安全风险最低值；Z1为运输费用函数；Z2为运输线路上风险函数；Z3为运输线路周边人员安全风险函数；λ为自备车运输收费占国铁车收费的比例；g1，g2分别为基价 1、基价 2；e(i,j)为运输弧 (i，j) 之间的里程，km；qk为货运需求k的运量，车；μ为自备车单车载重量，t；xk(i,j)表示自备车运输路径中是否包含运输弧 (i，j)，为 0-1 变量，取值为 1时，表示车辆运输路径包含该弧段，反之为不包含；P(i,j)为运输弧 (i，j) 的事故率；R(i,j)为运输弧 (i，j) 上的旅客运输密度；δ(i,j)为运输弧 (i，j) 周边的人口密度，人/km2；d为事故影响的直线距离，km；B(i,j)为国家规定的人员风险限制浓度；n(i,j)为运输弧 (i，j) 的列车中罐车的平均辆数，车；m(i,j)为弧段 (i，j) 的区间通过能力，列/d。

目标函数 ⑴ 表示自备车运输费用最小；目标函数 ⑵ 从减少铁路运输风险角度，表示运输线路上旅客的潜在风险最小；目标函数 ⑶ 从降低社会风险角度，表示运输线路周边的人员安全风险最低；约束 ⑷ 表示每一个节点的流平衡约束，当节点为车流k的终点时，表达式的取值为 1，表示该节点必有当前这 1 支车流流入，而没有车流流出，当节点为车流k的起点时，表达式的取值为-1，表示该节点必有当前这 1 支车流流出，而没有车流流入，当节点既非起点也非终点是，表达式取值为 0，表示该节点流入的车流量与流出的车流量相等；约束 ⑸ 表示一旦发生事故线路周边的危险物浓度应确保在国家规定的人员风险限制浓度内；约束 ⑹ 表示弧段罐车通过能力限制；约束 ⑺ 表示决策变量为 0-1 变量。

1.3 模型求解

采用线性加权法将多目标规划化为单目标规划问题，进而求解多目标规划最优值。由于不同目标函数的量纲及数量级不同，且试算表明运输费用、线路上客运流量干扰及线路周边影响的数值的数量级之比大致为 1 : 10 : 100 000，不能准确体现对运输费用及线路上客运流量的重视程度，因而采用改进的线性加权进行变换，其主要步骤为：①在忽略其他目标函数的影响、保留原有约束条件的情况下，分别求出每个单目标函数的最优值；②将各自单目标函数除以上一步求出的最优值，得到标准化后的目标函数，消除不同量纲及数量级的影响；③结合线性加权法，构建目标函数。在对不同的目标函数进行权重确定之后，构建的多目标规划目标函数可以转化为

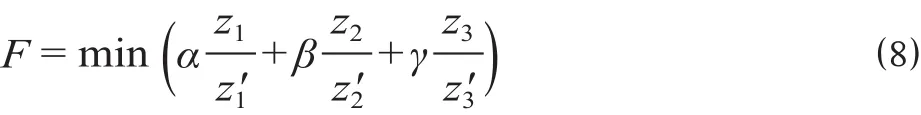
式中：F为最小化目标函数值；α，β，γ分别为各目标函数相应的权重，0≤α≤1，0≤β≤1，0≤γ≤1，α+β+γ= 1。

Lingo 软件是一种交互式的线性和通用优化求解器，可用于求解线性及非线性规划问题。选用Lingo 12.0 求解引擎编程求解，求解时输入为各相关参数及变量，输出为综合目标函数值及对应路径节点。

2 案例分析

选取 19 个城市、28 条弧段建立网络，以长治、聊城、邯郸、新丰镇为硫酸生产点，菏泽、潢川、商丘、南阳、洛阳、濮阳、阜阳为硫酸需求点，其余城市为中转节点，简化后得到运输路网如图2 所示。

2.1 基础数据

（1）OD 运量。长治、聊城、邯郸、新丰镇为硫酸生产点，菏泽、潢川、商丘、南阳、洛阳、濮阳、阜阳为硫酸需求点，其 OD 运量如表1 所示。

（2）目标函数参数取值。λ根据《铁路货物运价规则》，取值为 0.8；设定列车可在路网中任意车站之间的线路双向运行，各城市间的铁路距离e(i,j)通过站间里程表查询，设定自备车平均行驶速度为60 km/h，计算各弧段运行时间；自备罐车运输硫酸费用按 5 号运价，根据 95306 网站信息，5 号运价基价g1= 18.6 元/t，g2= 0.103 元/(t · km)；根据《全国铁路统计资料汇编 2015》，获取各区段旅客运输密度R(i,j)，其中未统计的区段按照区段间开行旅客列车列数估算；泄漏事故率P(i,j)在路网中不同弧段是不同的，根据 Glickman 等提出的运输泄漏事故率模型求弧段事故率[7]，事故率与路段上的每百万机车走行公里事故率及列车平均编成辆数相关，单位与每百万机车走行公里事故率一致，故可能大于 1；暴露区域人口与铁路沿线人口密度有关，是衡量铁路自备车运输路径风险的重要指标，采用暴露区域面积与区域内平均人口密度的乘积来估算影响区域的人口，通过查阅各城市统计年鉴计算得出路段的人口密度δ(i,j)，根据相关研究以腐蚀性物质影响的直线距离d= 0.8 km计算面积，即可算得暴露区域的人口；环境安全风险容量限制参照《大气污染物综合排放标准》[8]中有关规定，取一定空间内硫酸的允许浓度最大值B(i,j)为 70 mg/m3；根据《铁路技术管理规程》中的隔离标准并结合调研情况为一列车中不超过 18 辆，对各弧段每列车中自备罐车平均辆数n(i,j)进行设定，并调研得到通过能力m(i,j)；硫酸罐车载重量μ= 35 t/车。相关参数取值如表2 所示。

图2 运输路网图Fig.2 Transport network

表1 OD 运量Tab.1 Freight volume of OD

2.2 求解结果分析

结合表1、表2 提供的基础数据，将各参数取值代入自备车运输路径选择模型，将案例各变量取值输入 Lingo12.0 求解引擎，在模型运输费用、线路上风险、线路周边风险权重取α= 0.5、β= 0.25、γ= 0.25 时，可求解得到模型目标函数值及相应运输路径。案例求解结果如表3 所示。

由表3 可以看出，1 组、4 组、5 组、6 组、7 组综合路径与只考虑运输费用所选路径存在差异，2组、3 组、8 组综合路径与只考虑运输费用所选路径为同一条路径。为直观展示，在目标函数权重分别为α= 0.5、β= 0.25、γ= 0.25 时，对长治—潢川、聊城—南阳运输径路进行对比分析。长治—潢川运输路径对比如图3 所示，聊城—南阳运输路径对比如图4 所示。

从图3、图4 可以看出，长治—潢川避开了郑州、漯河等人口密集城市，聊城—南阳避开了京广线而选择了客运繁忙程度较低、人口相对较少的路线，且考虑风险的综合目标函数取值低于只考虑运费的综合目标函数值。

表2 相关参数取值表Tab.2 Value of parameter

3 结束语

基于安全风险的铁路自备车运输路径选择研究，以总运输费用最低、运输线路上旅客风险最小、线路周边人员风险最小为目标，构建车辆运输路径选择多目标 0-1 整数规划模型，可以有效地实现选择综合成本最优的路径。案例求解结果显示考虑风险情况下最优路径选择往往会避开人口密集区域与客运繁忙线路，表明风险对运输路径选择的影响。该研究不仅有利于铁路运输部门提高对运输安全风险的预防，营造更加环保、绿色的铁路运输环境，更有利于提高铁路的经济效益和社会效益，为普通国铁车辆运输路径选择提供参考。

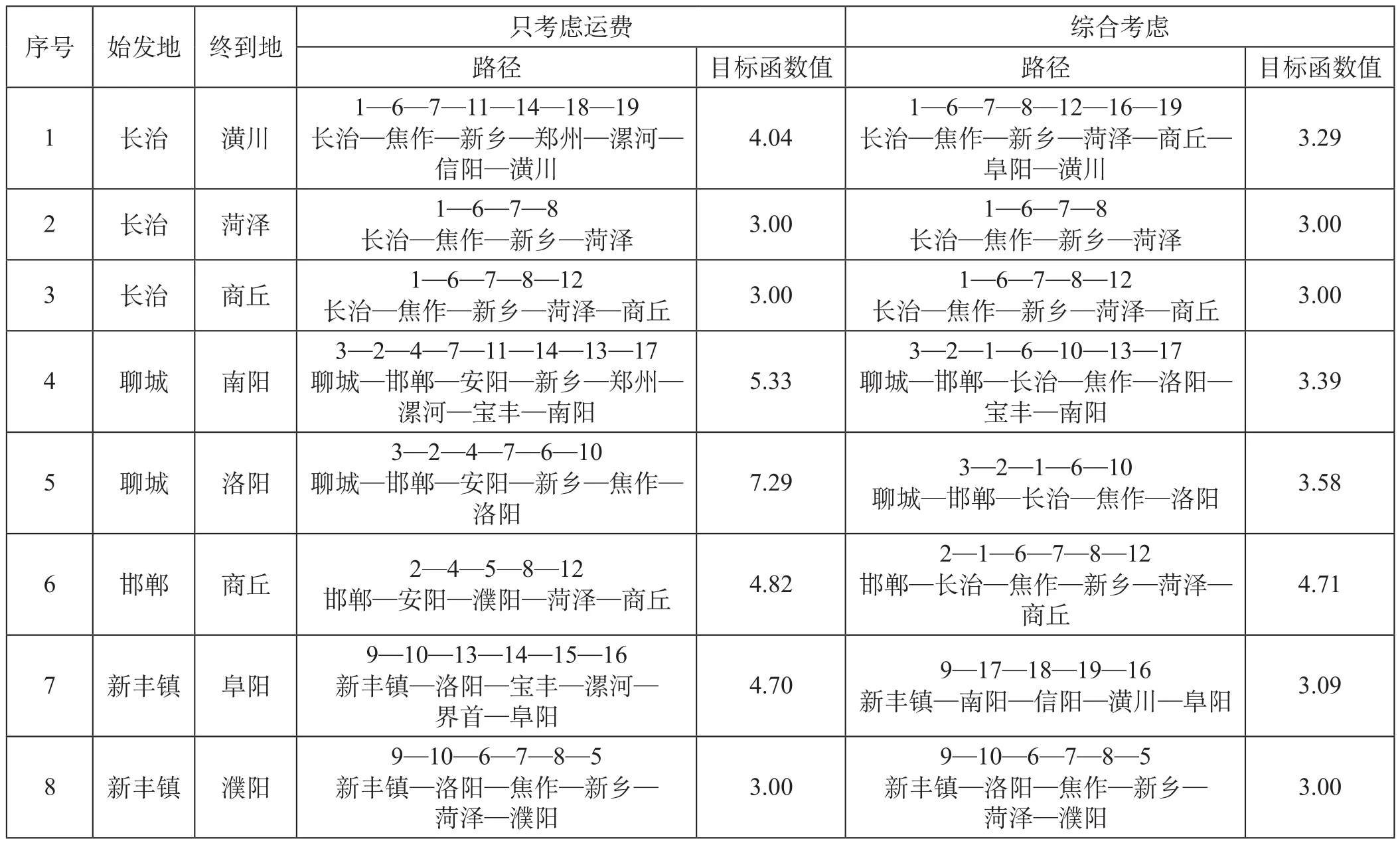
表3 案例求解结果Tab.3 Result of the case

图3 长治—潢川运输路径对比Fig.3 Route comparation between Changzhi and Huangchuan

图4 聊城—南阳运输路径对比Fig.4 Route comparation between Liaocheng and Nanyang

[1] 陈钢铁，帅 斌. 运输路径优化蚁群算法问题研究[J]. 铁道运输与经济，2010，32(9)：68-72.CHEN Gang-tie，SHUAI Bin. Research on Ant Colony Algorithm for Transport Route Optimization[J]. Railway Transport and Economy，2010，32(9)：68-72.

[2] 陈文强，吴群琪. 时间相关的运输网络最小费用路径模型及算法[J]. 铁道运输与经济，2009，31(5)：11-14.CHEN Wen-qiang，WU Qun-qi. Time-dependent Minimum Cost Path Modal and Algorithm of Transport Network[J].Railway Transport and Economy，2009，31(5)：11-14.

[3] YAN S，LANG M，WANG D. Bi-Objective Modelling for Hazardous Materials Road-Rail Multimodal Routing Problem with Railway Schedule-based Space-Time Constraints[J].International Journal of Environmental Research & Public Health，2016，13(8)：16-31.

[4] 陈 皓，彭其渊，王文宪. 铁路超限装载方案的运输路径选择研究[J]. 铁道运输与经济，2016，38(12)：74-79.CHEN Hao，PENG Qi-yuan，WANG Wen-xian. Path Selection and Loading Scheme for Out-of-Gauge Transportation[J]. Railway Transport and Economy，2016，38(12)：74-79.

[5] 崔发生. 铁路专用线货运安全管理的探讨[J]. 铁道货运，2017，35(3)：45-49.CUI Fa-sheng. Discussion on Freight Transport Safety Management of Railway Industrial Siding[J]. Railway Freight Transport，2017，35(3)：45-49.

[6] MADALA B P R. A Simulation Study for Hazardous Materials Transportation Risk Assessment[J]. Meteorological and Environmental Research，2000，77(8)：41-47.

[7] GLICKMAN T S. Benchmark Estimates of Release Accident Rates in Hazardous Materials Transportation by Rail and Truck[J]. Transportation Research Record，1988，1193(3)：22-28.

[8] 国家环境保护部，国家质量监督检验检疫总局. 大气污染物综合排放标准：GB16297-1996[S]. 北京：中国标准出版社，1997：4.