基于 SLIM-BN 的非正常条件下铁路接发列车人因可靠性分析
康毅军,郑云水,牛行通
(兰州交通大学自动化与电气工程学院,甘肃兰州730070)
1 基于SLIM-BN人因可靠性分析的原理与步骤
1.1 SLIM
SLIM[11-12]的实质是对行为形成因子 (PSF) 进行综合评价,涉及 2 个核心算法。

(1)量化若干个PSF对完成相应任务的影响度,即若干个成功似然指数 (SLI)。成功似然指数法认为,人完成任务的绩效很大程度上是依赖于执行任务时所处的情景环境因子,由此可构造相应的SLI,以表征PSF对完成任务的影响程度,其表达式为着我国铁路现代化建设的不断发展,各个车站的接发列车作业安全系数都在各方面取得显著提高[1-2],然而当系统处于设备故障、技术设备施工、自然灾害、不良天气等非正常条件时,工作人员受知识经验、工作应力、应急演练不足等因素的影响,发生人因失误的概率将比正常条件下显著增加[3]。国内和国外学者关于铁路接发列车作业人因可靠性研究较多。Melissa 等[4]利用人因素分析和分类系统 (HFACS) 分析了多起铁路行车事故。Read 等[5]通过对铁路行车人因事故分析,总结出技能型相关的失误与任务需求有关,规则型及知识型相关的失误与缺乏培训有关。Luca 等[6]用贝叶斯网络和模糊专家系统 2 种方法对人的可靠性进行了分析。吴海涛[7-8]分析了非正常条件下高速铁路调度指挥人因可靠性,并提出了一种改进的人因失误概率量化方法。从国内外的研究成果看,多数接发列车作业人因可靠性分析研究仍然处于经验阶段,而且在各种人的可靠性分析 (HRA) 的研究中或多或少存在缺陷,如缺乏人因可靠性分析数据、数据量化存在一定的片面影响而必须依靠专家的主观判断、人的心理特征和认知行为很难量化等[9-10]。为此,提出一种基于成功似然指数法 (SLIM) 与贝叶斯网络 (BN) 相结合 (SLIM-BN) 的非正常条件下铁路接发列车人因可靠性分析评价方法,通过风险评估与控制,以期实现对非正常条件下接发列车作业人员人因可靠性的定量分析。式中:SLIj为完成任务j的成功似然指数;Wi为第i种PSF归一化下的权重值,且Rij为在第i种PSF的作用影响下,完成任务j的可靠度。
(2)将SLI转化为任务的失败概率。任务的失败概率人因失误概率 (HEP) 转化公式为

式中:a,b为待定常数,可由已知的人因失误概率的 2 个边界点求得。
1.2 BN
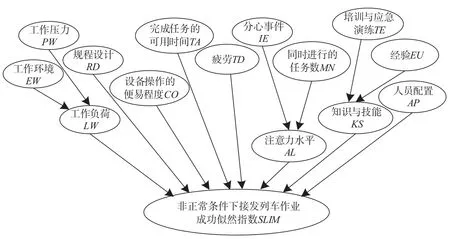
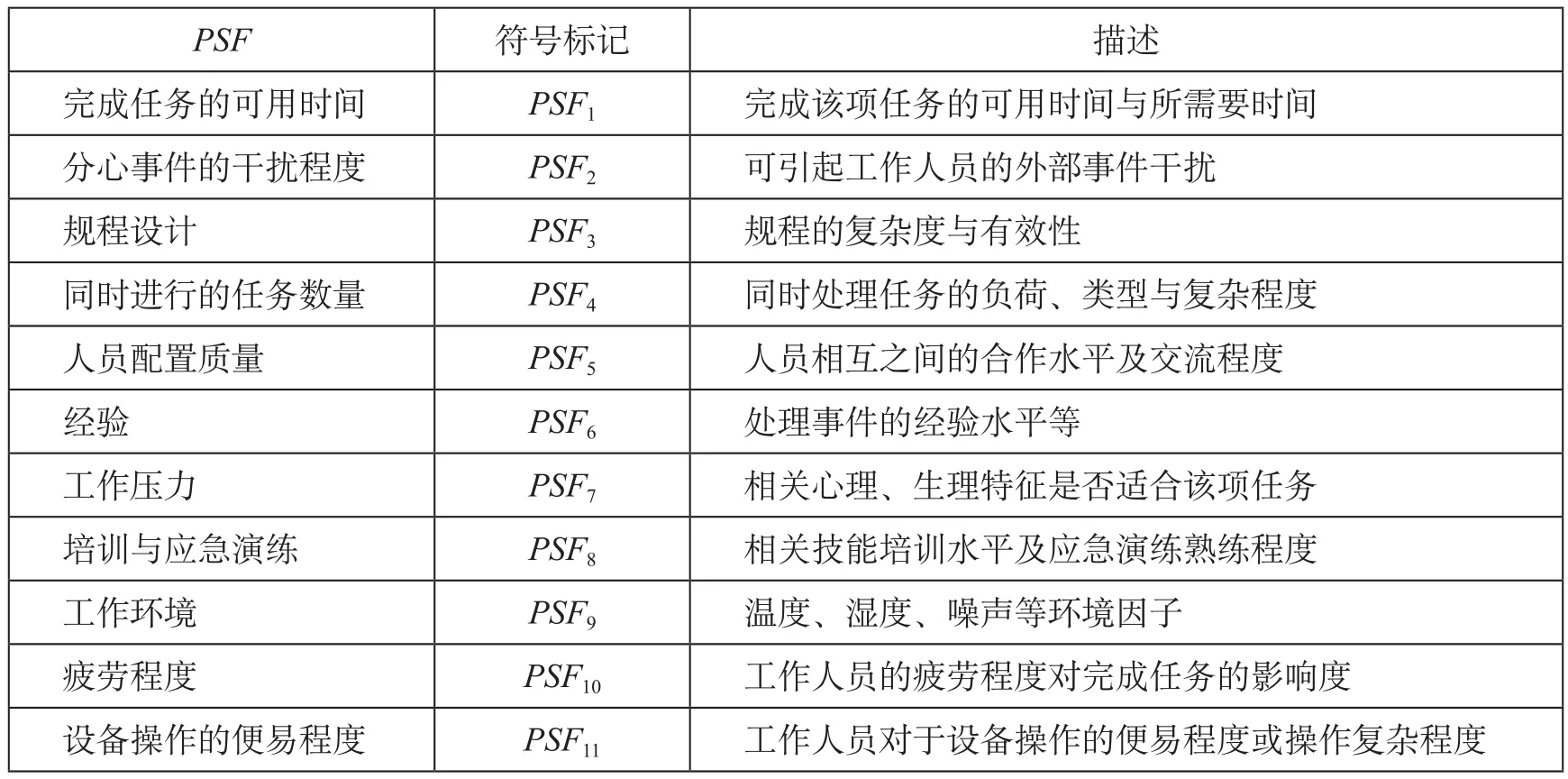
贝叶斯网络又称信度网络、概率因果网等[13-14],其原理是在一个拥有N个节点的贝叶斯网络中,可以用N= < (1)第一部分 (2)在根节点先验概率和非根节点条件概率已知条件下,可获得包含所有节点的联合概率分布如下。 Vi节点的边缘概率可表示为 由贝叶斯定理可知,在某事件发生的条件下,可以得到其他关联节点的概率分布,即 式中:e为与节点V相关联的事件,在进行贝叶斯推理时由已知条件给出其概率大小。 熵权计算法[15]可以量化评价指标的固有信息与专家决策者的主观信息,运用数学方法确定各评价指标的重要程度。评价指标的熵权值越大,表明该指标可以提供越多的有用信息,对评价结果产生的影响作用越大。考虑到人因失误指标数据本身的特性,选用客观熵权计算方法为指标赋权重值,步骤如下。 (1) 确定待评价对象i在评价指标j下的指标值比重Qi j。 式中:Fi j为评价对象i处于评价指标j下的指标值。 (2) 确定指标j的熵值h j。 式中:l为评价对象总数;n为每个评价对象的评价指标总数。 (3)确定指标j的熵权值w j。 SLIM 的核心算法一是一个主观性比较强的估计方法,因为影响工作人员行为的PSF,以及在各PSF影响下完成该任务的相对可靠度,均由专家的判断来确定。针对这一不足,采用贝叶斯网络弥补这一缺点,由于贝叶斯网络具有强大的不确定性问题的处理能力,可将专家先验知识和数据进行综合的理想表达,能在有限的、不完整的或不确定的信息下进行学习和推理。该方法主要分析步骤如下。 (1)PSF的识别与筛选。首先进行人因失误模型下的情景环境分析,其次在构建的PSF体系中筛选出重要的PSF。 (2)构建贝叶斯网络。将认知行为的SLI定义为网络的叶节点,PSF定义为网络的根节点和中间节点,建立贝叶斯网络的拓扑结构。 (3)确定节点变量的权重与先验概率及条件概率。考虑到人因失误指标数据本身的特性,用熵权计算法为节点赋权重值,然后在多位专家评估的基础上分别确定网络中节点变量的概率分布。 (4)进行贝叶斯推理与 SLIM 法计算。在贝叶斯推理计算得出SLI后,按照 SLIM 法中的核心算法二,进行人因失误概率的计算。 铁路非正常条件下的接发列车作业是行车组织的重要环节,它的工作性质决定了作业人员要长时间的精力集中,以此来保障铁路行车作业的正常、安全、有序运营。为全面了解非正常情况下人因可靠性影响因子,对某车站作业人员进行了调研和访谈,通过整理该调查资料得到非正常条件下接发列车工作人员PSF如图1 所示。 图1 非正常条件下接发列车工作人员 PSFFig.1 Staff PSF for arrival and departure of trains under abnormal conditions 在大量的 PSF 中,必定存在相互交叉的情况,而且可能会影响人因可靠性分析的准确性,因而应筛选有效的PSF,这样才能使分析结果更加准确。人因可靠性PSF筛选标准如下:尽量完整地把握对认知行为重要的PSF;尽可能地避免PSF之间的交叉影响;尽量筛选出能直接影响人行为失误的灵敏因子;筛选出的灵敏因子要能进行可靠性分析;筛选出的灵敏因子要能够进行评价;筛选那些较容易理解的术语描述因子。 在非正常状况下的人因可靠性影响因素和某车站多位工作人员调研资料分析的基础上,参照人因可靠性PSF筛选标准得到非正常条件下接发列车作业人员的主要的PSF如表1 所示。 图2 非正常情况下铁路接发列车作业人员 SLIM-BN 模型Fig.2 SLIM-BN model of the arrival and departure of trains under abnormal conditions 根据前述分析,构建非正常情况下铁路接发列车作业人员可靠性分析 SLIM-BN 模型如图2 所示。 在建立的模型基础上,根据贝叶斯推理计算,则可得到SLI。将求得的SLI和人因失误概率的上下限代入公式 ⑵,就可得到人因失误概率。 构建如图2 所示的 SLIM-BN 模型后,运用熵权计算法对各节点变量赋权重值。由于人因失误指标本身的特点,结合 4 位专家根据非正常情况下接发列车的实际情况,对 SLIM-BN 模型中 11 个根节点指标PSF1-PSF11进行打分 (满分为 5 分),最终确定决策初始判定矩阵为 表1 非正常条件下接发列车作业人员的主要 PSFTab.1 Main PSF for arrival and departure of trains under abnormal conditions 计算根节点指标PSF1-PSF11的熵权值,根据公式 ⑺ 至公式 ⑼ 提出的熵权计算法得到每个根节点指标的熵权值为 W= (0.094 3,0.075 2,0.092 7,0.076 8,0.066 2,0.107 4,0.088 6,0.109 8,0.085 5,0.109 6,0.093 9) 计算各根节点指标的概率分布,通过对某铁路局实地调研,整理出全铁路局 2012—2016 年的人因失误数据统计表,并从中筛选出非正常条件下接发列车作业人因失误的数据,再结合多位专家评估与计算得到的每个根节点指标的熵权值,最终获得其根节点的变量状态与先验概率如表2 所示,中间变量“工作负荷”“注意力水平”和“知识与技能”的条件概率如表3 至表5 所示。 表2 根节点的变量状态与先验概率Tab.2 Variable state and prior probability of the root node 表3 中间变量“工作负荷”的条件概率 (工作负荷/工作环境,工作压力)Tab.3 Conditional probability of intermediate variable “workload” (workload/working environment, working pressure) 表4 中间变量“注意力水平”的条件概率(注意力水平/分心事件,同时进行的任务数)Tab.4 Conditional probability of intermediate variable “attention level” (attention level/distraction event, simultaneous task number) 贝叶斯的因果推理是根据各个节点的状态及其概率,应用贝叶斯定理,推导出结果发生的可能性。在此结合 SLIM-BN 模型,利用微软开发的贝叶斯建模工具 (MSBN) 软件,构建贝叶斯网络进行概率推理,计算各根节点在最佳状态时的非正常情况下铁路接发列车作业的SLI值为 0.933 85。 表5 中间变量”知识与技能”的条件概率(知识与技能/培训与应急演练,经验)Tab.5 Conditional probability of intermediate variable “knowledge and skills” (knowledge and skills/training and emergency drill, experience) 同理可计算所有节点变量处于一般状态和最差状态下,非正常情况下铁路接发列车作业的SLI为(0.893 86,0.840 21)。根据专家调研与数据统计确定的非正常铁路接发列车任务的人因失误概率上下限为 (0.01,0.2),带入公式 ⑵,得到a=-13.894,b= 10.975。将在一般状态下非正常条件下接发列车作业人员的SLI= 0.893 86代入公式 ⑵,可以求得在一般状态时非正常条件下铁路接发列车任务的人因失误概率为HEP= 0.035 95。 贝叶斯诊断推理是一种逆推理过程,其原理是在结果发生之后,依据所构建的贝叶斯网络模型,进行逆向的诊断推理过程,分析其事故可能发生的原因。如果已经发生非正常条件下接发列车作业人因失误,根据建立的贝叶斯网络模型,则可求得各因子的后验概率。将求得的各因子处在最不利的状态下,比较其后验概率与先验概率的大小,变量的先验概率与后验概率比较如表6 所示。 表6 变量的先验概率与后验概率比较Tab.6 Contrast between the prior probability and the posterior probability of the variable 由表6 可知,发生非正常情况下接发列车人因失误时,“培训与应急演练”“疲劳程度”“经验”和“完成任务的可用时间”因子处在最不利状态的时候,它们的先验概率和后验概率变化程度较大。由此得出,节点“培训与应急演练”“疲劳程度”“经验”和“完成任务的可用时间”因子敏感度较高,对人因可靠性的影响相应较大,即这些敏感因子很可能会引起人因失误。为保障安全有序地进行接发列车作业,应当从这 4 个方面加强培训或采取相关有效的措施来提升工作人员的知识与技能。 在人因可靠性分析模型中,结合成功似然指数法与贝叶斯网络的方法量化人因差错概率HEP,不但克服了 HRA 方法中传统计算HEP的局限性,而且也提高了人因可靠性分析的质量。在建立的BN 模型中,通过应用 BN 的因果推理,得出结果后再进行 SLIM 的计算,最终得到完成该任务的可靠度,以此使人因可靠性结果更加可信,并且通过某车站的实际案例,有效识别出人因失误的主要贡献因子,即主要原因有“培训与应急演练”“疲劳程度”“经验”和“完成任务的可用时间”等。因此,在实际作业过程中,应当重点防范,并且制订相应的风险控制措施。以上研究表明,该SLIM-BN模型适用于非正常条件下铁路接发列车作业人因可靠性的分析,对于制定非正常接发列车作业规章制度具有一定的指导意义。 [1] 王 波,何世伟,焦文根,等. 铁路车务系统安全心里和行为模式的探讨[J]. 铁道运输与经济,2016,38(1):63-67.WANG Bo,HE Shi-wei,JIAO Wen-gen,et al. Discussion on Safety Mentality and Behavioral Patterns of Train Crew System[J]. Railway Transport and Economy,2016,38(1):63-67. [2] 韩 勇. 铁路超限货物运输安全影响因素评价[J]. 铁道货运,2017,35(5):10-15.HAN Yong. Evaluation of Factors Influencing the Safety of Railway Out-of-gaugeGoods Transportation[J]. Railway Freight Transport,2017,35(5):10-15. [3] 赵文江. 如何加强非正常情况下铁路车站接发列车的安全管理[J]. 科技展望,2016,26(20):193.ZHAO Wen-jiang. How to Strengthen the Safety Management of Arrival and Departure of Trains under Abnormal Conditions[J]. Prospect of Science and Technology,2016,26(20):193. [4] BAYSARI M T,MCLNTOSH A S,WILSON J R.Understanding the Human Factor Contribution to Railway Accident and Incident in Australia[J]. Accident Analysis and Prevention,2010,40(17):50-57. [5] READ G J,LENNE M G,MOSS S A. Associations between Task,Training and Social Environmental Factors and Error Types Involved in Rail Incidents and Accidents[J].Accident Analysis & Prevention,2012,48 (48):416-422. [6] BARALDI P,PODOFILLINI L,MKRTCHYAN L,et al. Comparing the Treatment of Uncertainty in Bayesian Networks and Fuzzy Expert Systems Used for a Human Reliability Analysis Application[J]. Reliability Engineering and System Safety,2015,138(2):176-193. [7] 吴海涛. 非正常条件下高铁列车调度指挥人因可靠性研究[D].成都:西南交通大学,2014.WU Hai-tao. Research on Human Reliability of High Speed Train Dispatching Command under Abnormal Conditions[D].Chengdu:Southwest Jiaotong University,2014. [8] 李鹏程,王以群,张 力. 人误原因因素灰色关联分析[J].系统工程理论与实践,2006,26(3):131-134.LI Peng-cheng,WANG Yi-qun,ZHANG Li. Gray Relational Analysis of Human Factors[J]. System Engineering Theory and Practice,2006,26(3):131-134. [9] MALAKIS S,KONTOGIANNIS T,KIRWAN B. Managing Emergencies and Abnormal Situations in Air Traffic Control:part I:Task Work Trategies[J]. Applied Ergonomics,2010,41(4):620-627. [10] MALAKIS S,KONTOGIANNIS T,KIRWAN B. Managing Emergencies and Abnormal Situations in Air Traffic Control:Part II:Teamwork Strategies[J]. Applied Ergonomics,2010,41(4):628-635. [11] PARK K S,LEE J I. A New Method for Estimating Human Error Probabilities:AHP-SLIM[J]. Reliability Engineering &System,2008,93(4):578-587. [12] 王黎静,王彦龙. 人的可靠性分析-人因差错风险评估与控制[M]. 北京:航空工业出版社,2015. [13] TRUCCO P,CAGNO E,RUGGERI F. A Bayesian Belief Network Modeling of Organizational Factors in Risk Analysis:A Case Study in Maritime Transportation[J].Reliability Engineering & System Safety,2008,93(6):845-856. [14] GROTH K M,SWILER L P. Bridging the Gap between HRA Research and HRA Practice:A Bayesian Network Version of SPAR-H[J]. Reliability Engineering & System Safety,2013,115(7):33-42. [15] 鲍新中,张建斌. 基于粗糙集条件信息熵的权重确定方法[J]. 中国管理科学,2009,3(17):131-135.BAO Xin-zhong,ZHANG Jian-bin. A Method for Determining Weights based on Conditional Information Entropy of Rough Sets[J]. Chinese Management Science,2009,3(17):131-135.


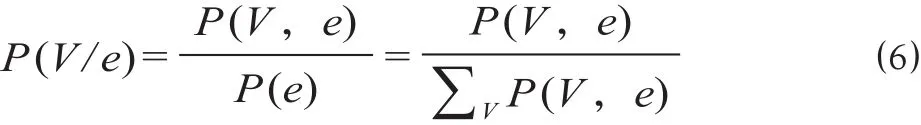
1.3 熵权计算法



1.4 基于 SLIM-BN 的人因可靠性分析步骤
2 非正常条件下铁路接发列车作业人员SLIM-BN模型
2.1 非正常条件下铁路接发列车作业人员可靠性影响因素

2.2 PSF 筛选
2.3 非正常条件下接发列车作业人因 SLIM-BN 模型构建
3 非正常条件下接发列车作业人员人因可靠性分析实例
3.1 确定节点变量的权重与先验概率及条件概率




3.2 贝叶斯的因果推理

3.3 人因失误概率计算
3.4 贝叶斯诊断推理

4 结束语

