Instability Analysis of Positron-Acoustic Waves in a Magnetized Multi-Species Plasma

M.A.Hossen,M.G.Shah,M.R.Hossen,and A.A.MamunDepartment of Physics,Jahangirnagar University,Savar,Dhaka-34,Bangladesh

2Department of Physics,Hajee Mohammad Danesh Science and Technology University,Dinajpur-5200,Bangladesh

3Department of General Educational Development,Daffodil International University,Sukrabad,Dhaka-1207,Bangladesh

1 Introduction

In contrast with the past,there has been continual attention in quantum plasmas in ultra-dense astrophysical systems[1−9]as well as laboratory plasmas.[10−12]The quantum effects become noticeable on the study of electron-positron(EP)plasmas which exist in the pulsar magnetosphere,[13−14]active galactic nuclei,[15]in the early universe,[16]etc.,and in laboratory situations.[17−18]In most of the cases,the EP plasma is supposed to exist in relativistic regimes,[19]and most of the theoretical investigations on the nonlinear structures in EP as well as electron-positron-ion(EPI)plasma medium have been done considering the relativistic cases.[20−21]Positrons are created in the interstellar medium when the atoms become interacted by the cosmic ray nuclei.[22]The data obtained during the alpha magnetic spectrometer flight permitting to probe the radiation belts in the Earths innermost magnetosphere provided an evidence of the presence of positrons.[23−24]In order to study the collective behavior of a plasma containing electrons and positron,it is necessary to find the condition to neglect the annihilation process.Many authors have neglected the annihilation process in the ultra-relativistic dense plasmas.[25−26]

Many astrophysical environments(viz.neutron stars,white dwarfs,etc.) where Fermi energy of the plasma species becomes comparable to or higher than their rest mass energy,show an unavoidable dependency on relativistic effects of plasma components.[27−30]The density of such a compact objects turned into so high that prevents gravitational collapse through the presence of degenerate pressure.Perhaps,there is a dramatic increase in energy of the accelerated particles to generate electrons and positrons by virtue of colliding these high-energy particles.For such an interstellar compact object,the degenerate pressure for the cold positron fluid can be given by the following equation,

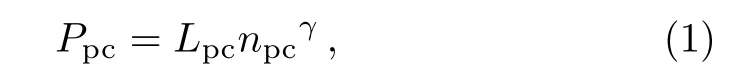
where

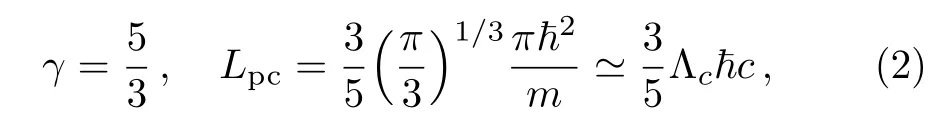
for the non-relativistic limit(where Λc=πħ/mc=1.2 ×10−10cm,and ħ is the Planck constant divided by 2π).While for the electron and hot positron fluids,

where for the non-relativistic limit[31−35]

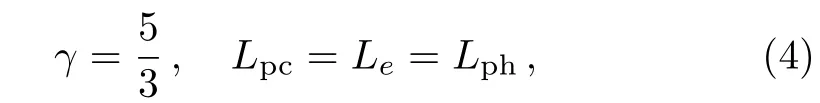
and for the ultra-relativistic limit[31−35]

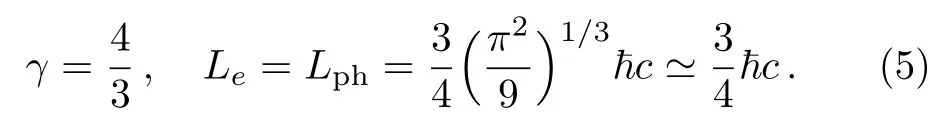
Presently,a considerable attention has been drawn to study the PA waves in astrophysical dense EPI plasmas containing distinct group of positrons(i.e.cold positrons and/or hot positrons).[36−38]The coexistence of cold and hot positron populations in pulsar magnetosphere has been predicted by Bharuthram.[39]In two temperature EPI plasma the interesting phenomena differing from that of one temperature can exist.Furthermore,in contrast to the case of the pure EP plasma,in two temperature EPI plasma the modulational instability may occur.Therefore,the prediction of existing cold and hot positrons species becomes momemtous to know the novel electrostatic perturbations as well as multi-dimensional instability in magnetized EPI plasmas.Basically,PA waves are the result of two distinct positron components(cold positron and hot positron)at different temperatures.The cold positron mass provides the inertia whereas the hot positrons and hot electrons provide the essential thermal pressure to develop the restoring force for the existence of PA waves.It is typically high frequency waves in comparison with the ion plasma frequency propagating at a phase speed which lies between the hot and cold positron thermal velocities.On the PA wave time scale,the ions are generally assumed stationary forming a neutralizing background.This means that the ion dynamics does not in fluence the PA waves because the PA wave frequency is much larger than the ion plasma frequency.

The nonlinear propagation of IA,PA and Electronacoustic waves for the relativistic plasma has been theoretically studied by a number of authors.[38,40−52]El-Shamyet al.[38]numerically investigated the in fluences of the cold/hot positron parameters on the phase shifts in a plasma system consisting of cold positrons,immobile ions,electrons,and hot positrons.Sahu[44]examined the planar and nonplanar PA shock waves in an unmagnetized EPI plasma system(containing mobile cold positrons,stationary positive ions,and Boltzmann-distributed electrons and hot positrons),and showed the effects of the ion kinematic viscosity,and Boltzmann-distributed electrons and hot positrons on PA shock waves.In a relativistically degenerate magnetoplasma,Ali and Rahman[53]investigated IA waves and numerically shown that the IA solitons and shocks are signi ficantly in fluenced by various parameters of plasma system.

However,all of these theoretical investigations[38,40−45]on the PA waves are accomplished in an unmagnetized EPI plasma system,and the effect of magnetic field or obliqueness is ignored.The Zakharov–Kuznetsov(ZK)equation and it’s solitary wave solution have been derived using the reductive perturbation method in a magnetized EPI plasma(consisting of inertial cold positrons,negatively charged immobile heavy ions,degenerate electrons,and hot positrons).Their multi-dimensional instability are also studied by the small-k(long-wavelength plane wave)perturbation expansion method.The effects of relativistic electrons/hot positrons degenerate pressure,obliqueness,etc.on the width,amplitude,and phase speed of the PASWs have been studied.

The article is organized in the following way.The normalized governing equations are presented in Sec.2.The ZK equation and it’s stationary solitary wave solution are derived on Sec.3.The instability of the PASWs(linear wave analysis)has been analyzed in Secs.4 and 5.The parametric investigations of our plasma systems is given in Sec.6.Finally,this paper ends up with the conclusion which is given in Sec.7.

2 Governing Equations

We consider the propagation of low-frequency PASWs in a four components magnetized EPI plasma(containing inertial cold positrons,negatively charged immobile heavy ions,degenerate electrons,and hot positrons).At equilibrium,the quasi-neutrality condition readsnpc0+nhp0=ne0+Zini0,wherenpc0,nhp0,ne0,andni0are the equilibrium densities of the cold positrons,hot positrons,electrons and ions,respectively andZiis the ion-charged state.In our present work,we have considered the effects that come from degenerate pressure only;not any quantum effects related to any particular components.For this reason,quantum effect terms i.e.,Bohm potential,quantum spin effects,etc.are ignored in Eqs.(6)and(7).In some other works,[54−55]authors have taken into account Bohm potential associated with particular plasma components such as electrons and positrons.Authors may consider typical parameters instead of the normalized parameters but that is beyond the scope of the present work.It is notable that the mass of cold positron is exactly the same as that of hot positron and electron,but their temperatures are different.The temperature of the cold positron is assumed to be very small,and in our present work it is neglected compared to the temperatures of hot positrons and electrons.So,we consider inertial cold positron,and define the waves associated with the inertial cold positron fluid as the PASWs.The model,what we have considered,is magnetized and since cold positron gives the inertia of this system so that we provide the magnetized equation for the cold positron only.Furthermore,the magnetized cold ion or cold positron or cold electron is common in Refs.[56–59].

The phase velocity of the PASWs is assumed to be much larger than the cold positrons thermal velocity and much less than the electrons/hot positrons thermal velocities,i.e.vTpc≪ω/κ≪vTph/vTe.In addition,electrons and hot positrons are considered to be inertialess and move almost parallel to the external magnetic field direction and negatively charged immobile heavy ions participate only to maintain the quasi-neutrality conditon.Under these situations,the basic set of nonlinear dynamic equations for magnetized cold positrons are governed as follows:

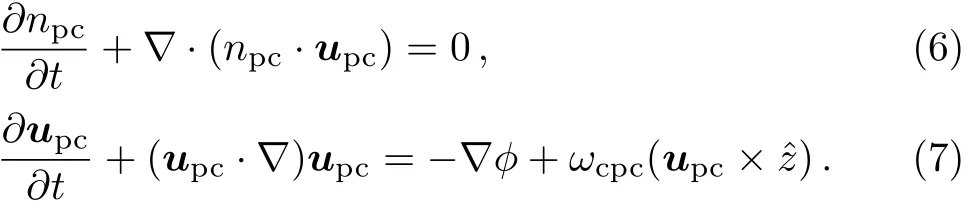
The momentum equations for inertialess degenerate electrons and hot positrons are given by

The Poisson equation is written as

wherenpc(ns)is the cold positron(hot positron/electron)number density normalized by its equilibrium valuenpc0(nph0/ne0);upcis the cold positron fluid speed normalized byCpc=(msc2/mpc)1/2,ms(mpcandme)being the rest mass of species(cold positron and electron);jrepresents the charge state of plasma species(i.e.j=1 for electron andj=−1 for hot positron);cbeing the speed of light in vacuum;ϕis the electrostatic wave potential normalized bymec2/e,ebeing the magnitude of the charge of an electron;the time variabletis normalized byωpc−1=(mpc/4πe2npc0)1/2,and the space variable is normalized byλD=(mec2/4πe2npc0)1/2,respectively.Hereα=ne0/npc0,σ=nph0/npc0,µ=ni0/npc0,andωcpcbeing the cold positron cyclotron frequency(eB0/mpcc)normalized byωpc−1,andKs=nγ−1s0Ls/msc2,respectively.

3 Derivation of Z-K Equation

To derive the ZK equation for describing the nonlinear propagation of the PASWs in the EPI plasma under consideration,we use Eqs.(6)–(9),and employ the reductive perturbation technique.[60]We first introduce the stretched coordinates as

whereϵis a small parameter measuring the weakness of the dispersion,Vpis the linear phase speed normalized by the PASWs speed(Cpc).It may be noted here thatX,Y,andZare all normalized by the Debye radius(λD),andτis normalized by the ion plasma periodWe next expand the quantities about their equilibrium values in a power series ofϵas[60−61]

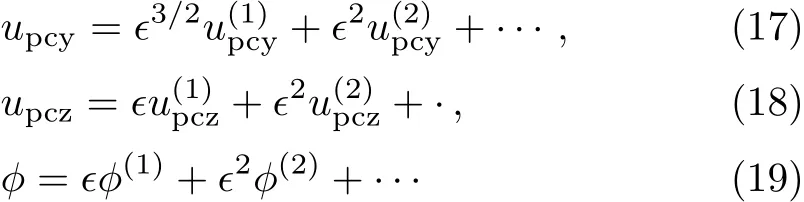
Now,using Eqs.(10)–(19)into Eqs.(6)–(9),taking the lowest order coeきcient ofϵ,we can write

whereK′=γKand Eq.(23)is the phase speed of the PA waves propagating in the magnetized EPI plasma under consideration.It is seen thatVpdecreases(increases)with the increase of the electron number density(cold positron number density).The first orderXandY-components of Eq.(7)can be written as

Equations(24)and(25)represent theXandYcomponents of the cold positron electric field drifts.These equations are also satis fied by the second order continuity equation.Again,using Eqs.(10)–(19)into Eqs.(6)–(9),and eliminatingandthe next higher orderXandYcomponents can be found as

Equations(26)and(27)represent theXandYcomponents of the cold positron polarization drifts.Now,following the same procedure one can obtain the next higher order continuity equation,andZcomponent of the momentum equation.Using these new higher order equations along with Eqs.(20)–(28),one can eliminateandϕ(2),and finally obtain

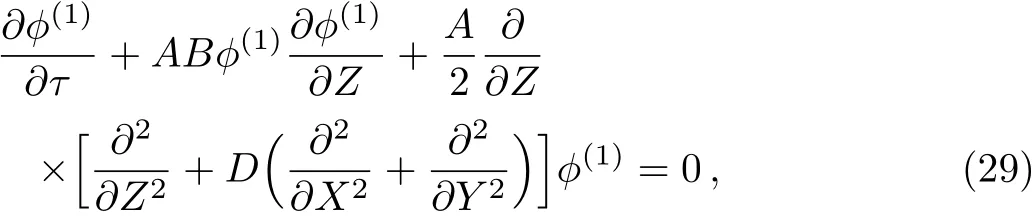
where

Equation(29)is the ZK equation describing the nonlinear propagation of the PASWs in a magnetized EPI plasma with degenerate relativistic electron and hot positron fluids.

The stationary SWs solution of the ZK equation can be written as

whereψm=3U0/δ1is the amplitude,andis the inverse of the width of the solitary waves.The PASWs with positive(negative)potentialψm＞0(ψm＜0)is found forB＞0(B＜0)for the permissible value of any parameter.

4 Instability of the SWs

The instability of the obliquely propagating PASWs is studied by adopting the method of small-kperturbation expansion.[62−66]We first assume that

for a long-wavelength plane wave perturbation in a direction with direction cosines(lζ,lη,lξ),ψcan be written as

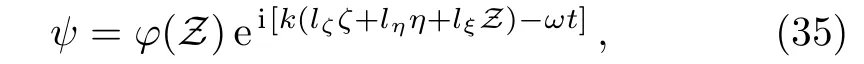
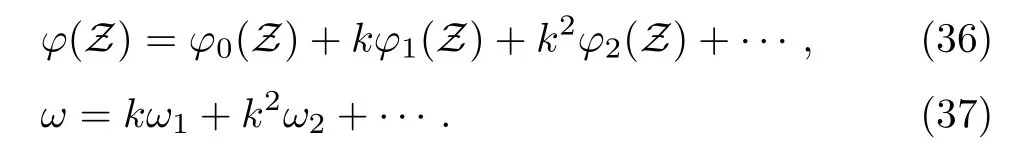
After some algebric calculation the linearized ZK equation can be expressed as

We have to find the expression ofω1by solving the zeroth,first,and second-order equations obtained from Eqs.(35)–(38).After integration,we can write the zeroth-order equation as

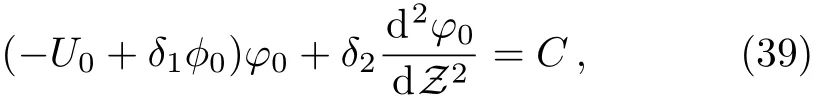
whereCis an integration constant.The solutions of the homogeneous part of the Eq.(38)can be written as

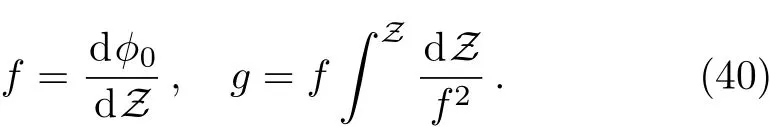
So,the general solution of this zeroth-order equation is as

whereC1andC2are two integration constants.Now,evaluating all integrals,the general solution of this zerothorder equation,forφ0not tending to±∞ as Z → ±∞,can finally be simpli fied to

The first-order equation,i.e.the equation with terms linear ink,obtained from Eqs.(35)–(38),and(42),after integration,it can be expressed as

whereKis another integration constant,andα1andβ1are given by

Now,following the same procedure,the general solution of this first-order equation,forφ1not tending to ±∞ as

Z→±∞,can be written as

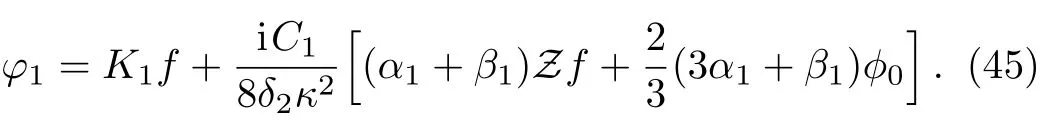
The second-order equation,i.e.the equation with terms involvingk2,obtained from Eq.(38)after substituting Eqs.(35)–(37),can be written as

where

The solution of this second-order equation exists if the right-hand side is orthogonal to a kernel of the operator adjoint to the operator

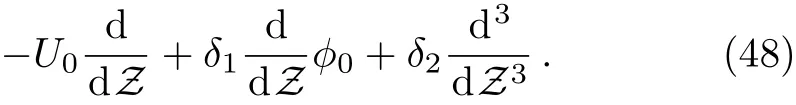
This kernel,which must tend to zero as Z→ ±∞,isϕ0=ϕmsech2(κZ).Thus we can write the following equation determiningω1as follows

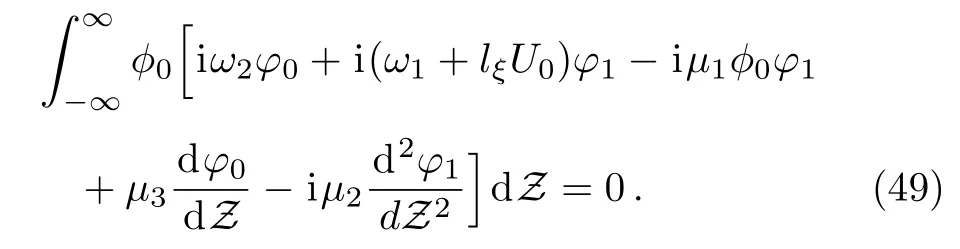
Now,substituting the expressions forφ0andφ1given by Eqs.(48)and(51),and after integration,we arrive at the following dispersion relation

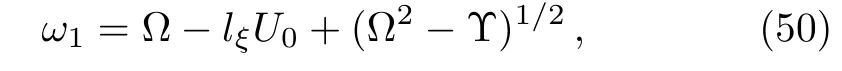
where

It is clear from the dispersion relation(50)that there is always instability if(Υ− Ω2)＞0.Thus,using Eqs.(32),(36),(44),(47),(51),and(52),one can express the instability criterion as[67−68]

whereSican be expressed as

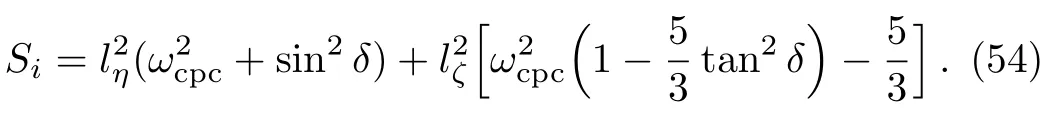
If this instability criterionSi＞0 is satis fied,the growth rateof the unstable perturbation of these PASWs is given by

Equation(55)represents that the growth rate(Γ)of the unstable perturbation is a linear function of PASWs speed(U0),but a nonlinear function of the propagating angle(δ),cold positron-cyclotron frequency(ωcpc)and direction cosines(lζandlη).

5 Linear Wave Analysis

We have derived the linear dispersion relation for PASWs to evaluate the characteristics of the linear waves.By linearizing equation(29),we can write

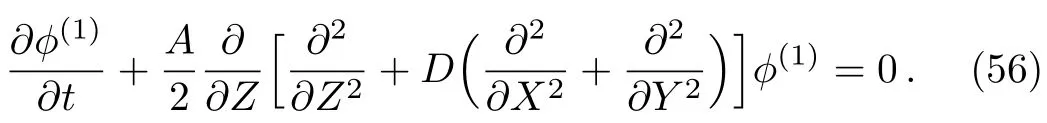
We assume that the variation of the dispersion relation(ω/k)in the transverse dimensions(theXandYdirections)is much slower than that of theZdirection.Afterward,we can neglect the transverse dimensions,i.e.,∂/∂X=∂/∂Y−→ 0.Then from Eq.(61),

We first consider that perturbation varying asϕ(1)∝e−(iω+ikZ)in the small amplitude limit to derive the dispersion relation.Now,from Eq.(62),the dispersion relation for the linear ZK equation is given by,

It is seen from the dispersion relation that PASWs signi ficantly modi fied by the the ratio of electron to cold positron number density(α),and with the ratio of hot positron to cold positron number density(σ).

6 Parametric Investigations

In this section,we will brie fly discuss the effects of the variation of the relative number densities such as the ratio of electron to cold positron number density(α),the ratio of hot positron to cold positron number density(σ),and the obliqueness(δ)of the magnetic field on the basic properties of the PASWs such as the amplitude(ψm),the width(Δ),and the instability.

6.1 Linear Properties

The dispersion relation which is shown in Eq.(63)is graphically represented in Fig.1.We find that the curve of the ultra-relativistic case is higher than that of the nonrelativistic case.The value ofωincreases more rapidly with the increase of the value ofkfor ultra-relativistic case than the non-relativistic case.

Fig.1 (Color online)The variation of the angular frequency(ω)with wave number(k)of the PASWs for the non-relativistic(red)and ultra-relativistic(blue)cases.

6.2 Nonlinear Properties

(i)Effect of electron to cold positron number density ratioα:

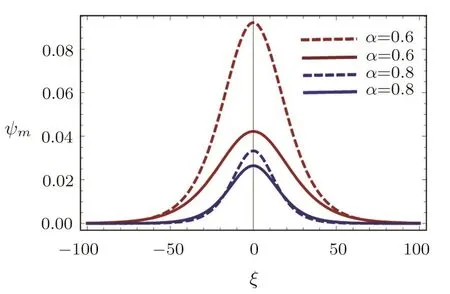
Fig.2 The variation of amplitude(ψm)of the PASWs for different values of α.The dashed curves are for the ultra-relativistic case where the solid curves are for the non-relativistic case.

The effect of electron to cold positron number density ratio(α)on the amplitude(ψm)of the PASWs pro file is shown in Fig.2.It is found that the variation ofψmfor ultra-relativistic(γ=4/3)case is higher than the nonrelativistic(γ=5/3)case.The variation ofψmfor different values ofαis depicted Fig.2.It is found that theψmdecreases(increases)with the increase of the value of electron number density(cold positron number density).The variation of Δ with respect to the variation ofδandαis shown in Figs.5 and 6.It has been clear from our observation thatψmas well as Δ is always greater for the ultra-relativistic case than the non-relativistic case.After reaching a certain value,Δ begins to decrease with the increase ofδ,and becomes zero atδ=90°.

(ii)Effect of hot positron to cold positron number density ratioσ:

The variation of the PASWs pro fileψmandξwithσis shown in Fig.3 for both non-relativistic and ultrarelativistic cases.It is seen thatψmdecreases with the increase of the value ofσ.The variation of Δ with respect to the variation ofδandσare depicted in Figs.7 and 8.The Δ increases withδand reaches to it is maximum value with increasing ofδ.After reaching a certain value it begins to decrease and becomes zero atδ=90°.It has been clear from our observation that Δ is always greater in ultra-relativistic case than the non-relativistic case.

Fig.3 The variation of amplitude(ψm)of the PASWs for different values of σ.The dashed curves are for the ultra-relativistic case where the solid curves are for the non-relativistic case.

(iii)Effect of obliqueness parameterδ:

It is assumed that the external magnetic field is directed along thez-axis,i.e.,B0=B0and the propagation is in thex–yplane.It is seen that the magnitude of the external magnetic field has no effect on the amplitude of the solitary waves.However,it does have an effect on the width of these solitary waves.The impact of the external magnetic fieldB0through cold positron cyclotron frequencyωcpcon the width of PASWs has been observed and found that the width of the K-dV soliton increases with the decreasing value ofωcpcfor the non-relativistic and the ultra-relativistic limits.It is shown that,as we increase the magnitude of the magnetic field,the width of these solitary waves decreases,i.e.the external magnetic field makes the solitary structures more spiky.The variation of Δ withδ(αandσ)for non-relativistic and ultrarelativistic case is represented in Fig.4(Figs.5–8).Δ increases with the increase of the value ofδ(from 0°− 55°)but begins to decrease for the values which lies within(55°− 90°).It should be mentioned here that the maximum obliqueness i.e.whenδ−→ 90°,the Δ−→ 0 andψmbecomes∞.So,the assumption that are electrostatic will no longer be valid,and fully electromagnetic theory is needed.

Fig.4 Comparison between width(Δ)and obliqueness parameter(δ)in considering non-relativistic(dotted curve)and ultra-relativistic(solid curve)cases.

Fig.6 The variation of width(Δ)of the potential associated with the PASWs with the obliqueness parameter(δ)and the ratio of electron to cold positron number density(α)considering ultra-relativistic case.

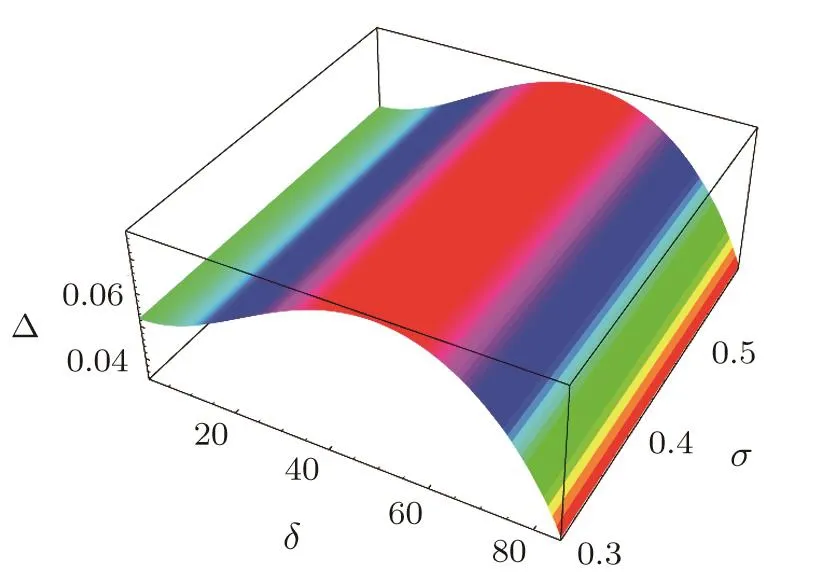
Fig.7 Showing the pro file of the PASWs along with the variation of the width(Δ)and the obliqueness(δ)with σ considering non-relativistic case.

Fig.8 Showing the pro file of the PASWs along with the variation of the width(Δ)and the obliqueness(δ)with σ considering ultra-relativistic case.

(iv)Instability of the PASWs:

We have graphically obtained the parametric regimes by theSi=0 surface plots(Figs.9–12)above which the PASWs become unstable,and below which the PASWs become stable.These show the variation of the parametric regimes which play an important role for the instability of the PASWs indicating that for the parameters above the surface,the PASWs become unstable.It is seen thatωcpcincreases with the increase of bothδandlζshown in Fig.9.The increment of the values ofδandlζgives a clear indication that the value ofωcpcincreases for which the PASWs become unstable.Si=0 surface plot showing the variation ofωcpcwithlζandlηforδ=15°which is represented in Fig.10.This indicates that as the value oflζandlηincrease,the value ofωcpcfor which the solitary waves become unstable decreases.The nonlinear variations of Γ withlζ,lη,ωcpc,andδare shown in Figs.11–12.The variation of Γ withlζ,andlηis depicted in Fig.11.It is clear from this that the unstable perturbation increases as the increasing of bothlζandlη.With the increasing of the values ofωcpcandδ,the value of Γ decreases which is depicted in Fig.12.It is found thatαandσhave no any effect on the instability or growth rate of the PASWs.

Fig.9 Plot Si=0.The variation of ωcpcwith δ and lζ for the parameter lη=0.10.

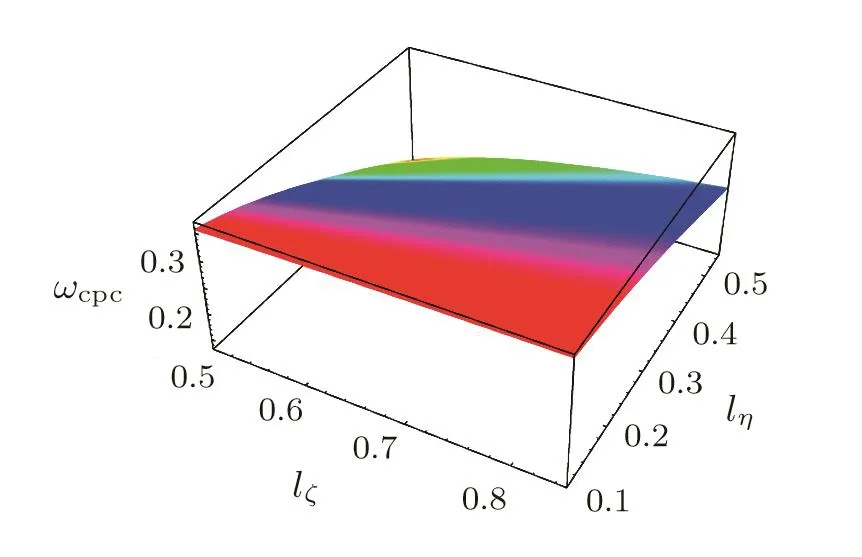
Fig.10 Plot Si=0.The variation of ωcpcwith lζ and lη for the parameter δ=15.

Fig.11 The variation of Γ with lζ and lη for the parameters U0=0.1,δ=15,ωcpc=0.80.

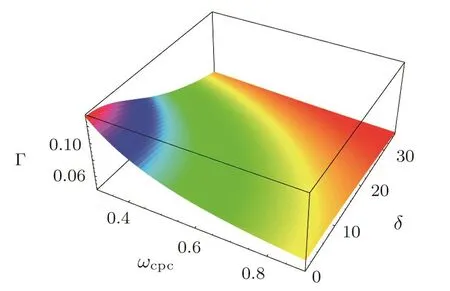
Fig.12 The variation of Γ with ωcpcand δ for the parameters U0=0.1,lη=0.70,and lζ=0.20.

7 Conclusion

To summarize,the propagation of the PASWs in amagnetized EPIplasma(containinginertialcold positrons, relativistic degenerate electrons and hot positrons,and negatively charged immobile heavy ions)has been theoretically investigated.We have studied the basic properties of the PASWs by analyzing the stationary solitary wave solution of the ZK equation,and finally analyzed the instability of these structures by small-k perturbation expansion method.

The solitary like structures,which we have predicted here,are due to balance between the nonlinearity and the dispersion,where the inertia comes from cold positron,and restoring force from the degenerate electron as well as hot positron.In our model,we used the following parameters for our numerical analysis,U0=0.01−0.1,σ=0.1−0.8,nso=1.0×1025−1030,δ=15,α=0.1−0.9,andµ=0.1 − 0.6[38,44]and for instability analysisωcpc=0.2 to 0.9,lζ=lη=0.1 to 0.9,andδ=0°to 90°.However,the ranges of the plasma parameters are very wide and relevant to many dense plasma environments.Finally,we hope that our present investigation may help to analyze the formation,and the basic characteristics of PASWs structures in a relativistic degenerate EPI plasma which occurs in space and many astrophysical situations,especially in pulsar environments.[38]

[1]M.Opher,L.O.Silva,D.E.Dauger,V.K.Decyk,and J.M.Dawson,Phys.Plasmas 8(2001)2454.

[2]S.Sadiq,S,Mahmood,Q.Haque,and M.Z.Ali,Astrophys.J.793(2014)27.

[3]J.Rafelski,L.Labun,and J.Birrell,Phys.Rev.Lett.110(2013)111102.

[4]S.Ahmad,Ata-ur-Rahman and S.A.Khan,Astrophys.Space Sci.358(2015)16.

[5]M.R.Hossen,L.Nahar,S.Sultana,and A.A.Mamun,High Energy Density Phys.13(2014)13.

[6]M.R.Hossen,L.Nahar,S.Sultana,and A.A.Mamun,Astrophys.Space Sci.353(2014)123.

[7]M.R.Hossen,L.Nahar,and A.A.Mamun,Phys.Scr.89(2014)105603.

[8]B.Hosen,M.G.Shah,M.R.Hossen,and A.A.Mamun,Euro.J.Plus 131(2016)81.

[9]B.Hosen,M.Amina,A.A.Mamun,and M.R.Hossen,J.Korean Phys.Soc.69(2016)1762.

[10]S.Datta and M.J.McLennan,Rep.Prog.Phys.53(1999)1003.

[11]S.C.Wilks,H.Chen,E.Liang,P.Patel,D.Price,B.Remington,R.Shepherd,M.Tabak,and W.L.Kruer,Astrophys.Space Sci.298(2005)347.

[12]N.Crouseilles,P.A.Hervieux,and G.Manfredi,Phys.Rev.B 78(2008)155412.

[13]P.Goldreich and W.H.Julian,Astrophys.J.157(1969)869.

[14]F.C.Michel,Rev.Mod.Phys.54(1982)1.

[15]H.R.Miller and P.J.Witta,Active Galactic Nuclei,Springer,Berlin(1987).

[16]W.Misner,K.S.Thome,and J.A.Wheeler,Gravitation,Freeman,San Francisco(1973).

[17]R.G.Greaves,M.D.Tinkle,and C.M.Surko,Phys.Plasmas 1(1994)1439.

[18]P.Helander and D.J.Ward,Phys.Rev.Lett.90(2003)135004.

[19]M.L.Burns,Positron-Electron Pairs in Astrophysics,American Institute of Physics,Melville,New York(1983).

[20]V.I.Berezhiani,M.Y.El-Ashry,and U.A.Mo fiz,Phys.Rev.E 50(1994)448.

[21]J.Zhao,J.I.Sakai,K.I.Nishikawa,and T.Neubert,Phys.Plasmas 1(1994)4114.

[22]O.Adrani,G.C.Barbarino,and G.A.Bazilevskaya,et al.,Nature(London)458(2009)607.

[23]E.Fiandrini,G.Esposito,B.Bertucci,B.Alpat,et al.,Space Weather 2(2004)S09S02.

[24]V.Plyaskin,Astropart.Phys.30(2008)18.

[25]W.F.El-Taibany and A.A.Mamun,Phys.Rev.E 85(2012)026406.

[26]E.W.Laing and D.A.Diver,Plasma Phys.Control.Fusion 55(2013)065006.

[27]S.L.Shapiro and S.A.Teukolsky,Black Holes,White Dwarfs and Neutron Stars:The Physics of Compact Objects,John Wiley&Sons,New York(1983).

[28]F.C.Michel,Theory of Neutron Star Magnetosphere,IL:Chicago University,Chicago(1991).

[29]M.A.Hossen and A.A.Mamun,Phys.Plasmas 22(2015)102710.

[30]M.A.Hossen,M.R.Hossen,S.Sultana,and A.A.Mamun,Astrophys.Space Sci.357(2015)34.

[31]S.Chandrasekhar,Philos.Mag.11(1931)592.

[32]S.Chandrasekhar,Astrophys.J.74(1931)81.

[33]M.R.Hossen and A.A.Mamun,Braz.J.Phys.44(2014)673.

[34]M.R.Hossen,L.Nahar,and A.A.Mamun,Braz.J.Phys.44(2014)638.

[35]M.A.Hossen,M.R.Hossen,and A.A.Mamun,Braz.J.Phys.44(2014)703.

[36]J.Srinivas,S.I.Popel,and P.K.Shukla,J.Plasma Phys.55(1996)209.

[37]I.J.Lazarus,R.Bharuthram,S.V.Singh,S.R.Pillay,and G.S.Lakhina,J.Plasma Phys.78(2012)621.

[38]E.F.El-Shamy,W.F.El-Taibany,E.K.El-Shewy,and K.H.El-Shorbagy,Astrophys.Space Sci.338(2012)279.

[39]R.Bharuthram,Astrophys.Space Sci.189(1992)213.

[40]M.G.Shah,M.R.Hossen,S.Sultana,and A.A.Mamun,Chin.Phys.Lett.32(2015)085203.

[41]M.G.Shah,M.R.Hossen,and A.A.Mamun,Braz.J.Phys.45(2015)219.

[42]M.G.Shah,M.R.Hossen,and A.A.Mamun,J.Plasma Phys.81(2015)905810517.

[43]M.G.Shah,A.A.Mamun,and M.R.Hossen,J.Korean Phys.Soc.66(2015)1239.

[44]B.Sahu,Phys.Scr.82(2010)065504.

[45]S.K.El-Labany,M.Shalaby,R.Sabry,and L.S.El-Sherif,Astrophys.Space Sci.340(2012)101.

[46]M.R.Hossen,S.A.Ema,and A.A.Mamun,Commun.Theor.Phys.62(2014)888.

[47]M.R.Hossen,L.Nahar,and A.A.Mamun,J.Astrophys.2014(2014)653065.

[48]M.R.Hossen,L.Nahar,and A.A.Mamun,J.Korean Phys.Soc.65(2014)1863.

[49]M.R.Hossen and A.A.Mamun,Plasma Sci.Technol.17(2015)177.

[50]M.A.Hossen,M.R.Hossen,and A.A.Mamun,J.Korean Phys.Soc.65(2014)1883.

[51]M.R.Hossen and A.A.Mamun,J.Korean Phys.Soc.65(2014)2045.

[52]S.A.Ema,M.R.Hossen,and A.A.Mamun,Contrib.Plasma Phys.55(2015)551.

[53]S.Ali and Ata-ur-Rahman,Phys.Plasmas 21(2014)042116.

[54]M.A.Hossen and A.A.Mamun,Phys.Plasmas 22(2015)073505.

[55]M.M.Hasan,M.A.Hossen,A.Rafat,and A.A.Mamun,Chin.Phys.B 25(2016)105203.

[56]Z.Zhenni,W.Zhengwei,L.Chunhua,and Y.Weihong,Plasma Sci.Technol.16(2014)995.

[57]M.Shahmansouri and H.Alinejad,Astrophys.Space Sci.347(2013)305.

[58]H.Alinejad and A.A.Mamun,Phys.Plasmas 18(2011)112103.

[59]M.Rahman,M.S.Alam,and A.A.Mamun,Astrophys.Space Sci.357(2015)36.

[60]H.Washimi and T.Taniuti,Phys.Rev.Lett.17(1966)996.

[61]P.K.Shukla and M.Y.Yu,J.Math.Phys.19(1978)2506.

[62]A.A.Mamun,Phys.Scr.58(1998)505.

[63]A.A.Mamun and R.A.Cairns,J.Plasma Phys.56(1996)175.

[64]E.Infeld,J.Plasma Phys.33(1985)171.

[65]M.G.M.Anowar and A.A.Mamun,Phys.Plasmas 15(2008)102111.

[66]S.Akter,M.M.Haider,S.S.Duha,M.Salahuddin,and A.A.Mamun,Phys.Scr.88(2013)015501.

[67]M.M.Haider and A.A.Mamun,Phys.Plasmas 19(2012)102105.

[68]M.M.Haider,Contrib.Plasma Phys.53(2013)234.