Numerical Investigation of Micropolar Casson Fluid over a Stretching Sheet with Internal Heating

Zaffar Mehmood, R.Mehmood,and Z.Iqbal

Department of Mathematics,HITEC University,Taxila,Pakistan

1 Introduction

Fluids with microstructures are termed as micropolar fluids.These fluids comprise of rigid,randomly oriented particles submerged in a glutinous medium.Micropolar lf uids find tremendous applications in blood,foodstuffs,polymers,liquid metal and alloys,plasma and drilling of oil and gas wells etc.Such type of fluid model contains non-symmetric stress tensors.Eringen[1−2]introduced the theoretical explanations of micropolar fluids and discovered the effects of micro motion of fluid elements.He proposed a logical and signi ficant overview of the classical Navier–Stokes model,covering,both in theory and applications,many more phenomena than the classical one.Moreover his generalization was well-designed and not too complex.Airmanet al.[3−4]presented a detailed review on application of fluids experiencing micro rotation at particle level.Khonsari and Brewe[5]examined the effects of viscous dissipation on lubrication characteristics of micropolar fluids.They reported that existence of microstructure,according to the micropolar theory,tends to enhance the load-carrying capacity and friction coeき-cient.Rotating micropolar fluid between parallel plates with heat transfer under the in fluence of transverse magnetic field has been investigated by Rashidet al.[6]They concluded that the micro rotation is an increasing function of coupling parameter,magnetic field and Reynolds number for strong concentration and it is a decreasing function of viscosity parameter.Nazaret al.[7]analyzed the stagnation point flow of a micropolar fluid over a stretching sheet.They carried out numerical investigation by employing Keller Box method.Non-Newtonian fluids have been an intense topic of research for the past few decades.Much focus had been given to the modeling and analysis of non-Newtonian fluids with rheological characteristics because of usage of various non-Newtonian fluids such as lubricants in industry.The non-linearity can manifest itself in a variety of ways in many fields,such as in food processing,drilling operations and bio-engineering.In this regard Ellahiet al.[8]presented numerical analysis of MHD steady non-Newtonian flows in presence of heat transfer and nonlinear slip effects.Similarly,Makindeet al.[9]analyzed unsteady flow of a reactive variable viscosity non-Newtonian fluid through a porous saturated medium with asymmetric convective boundary conditions and observe that there is a transient increase in both fluid velocity and temperature with an increase in the reaction strength,viscous heating and fluid viscosity parameter.Among the class of several other non-Newtonian fluid models,Casson fluid is one such model with yield stress characteristics.Casson fluid falls in the category of dilatant fluids.It is assumed that Casson fluid has an in finite viscosity at zero shear rates.If the applied shear stress is less than the yield stress then fluid behave like a solid and when shear stress applied is greater than yield stress fluid starts to move.Casson fluid model best fit to rheological data for numerous materials such as jelly,sauce,honey,soup and concentrated fruit juices,etc.[10]The presence of protein,fibrinogen and globulin in aqueous base plasma,red blood cells makes human blood an ideal example of Casson fluid.Number of researchers used Casson fluid to mathemati-cally model and examine the blood flow under a low shear rate in narrow arteries.Shahzadet al.[11]studied effects of mass transfer on generalized non-Newtonian fluid.They analyzed the in fluence of chemical reaction and suction on Casson fluid in presence of magnetic field.Nadeemet al.[12]observed analytically flow of Casson nano fluid.Mustafaet al.[13]discussed unsteady boundary layer flow of a Casson fluid due to an impulsively started moving flat plate.Similarly Bhattacharyaet al.[14]presented analytic solution for magneto hydrodynamic boundary layer flow of Casson fluid over a stretching/shrinking sheet with wall mass transfer.Heat transfer of viscous non-Newtonian fluids past a stretching sheet is a considerable problem in fluid dynamics.The problems arise in the field of engineering and metallurgy depends on hydrodynamic flow and heat transfer rate.In polymer technology,stretching plastic sheets are used in manufacturing products.In electrically conducting fluids,strips are used to control the cooling process.Chen[15]worked out laminar mixed convection of stretching sheet adjacent to vertical wall.Aliet al.[16]examined laminar mixed convection boundary layers induced by a linearly stretching permeable surface.Ishaket al.[17]inspected mixed convection boundary layers in the stagnation-point flow toward a stretching vertical sheet.The thermal effects in fluid flows may cause heat transfer effects in manufacturing processes.In these processes,thermal buoyancy force arises due to heating of a surface that may be in rest or moving continuously under some circumstances.Shateyiet al.[18]analyzed the effects of thermal radiation,hall currents,soret and dufour on MHD flow and heat and mass transfer in a micro polar fluid by mixed convection over stretching surfaces in porous media.Vajraveluet al.[19]studied the heat transfer in a viscous fluid over a stretching sheet with viscous dissipation and internal heat generation.Some more studies related to the current topic can be found in Refs.[20–31].

Most of researches have been carried out in micro polar fluids for characterizing the impact of magnetic field,heat transfer,mixed convection and viscous dissipation etc.To the best of our knowledge,micro polar fluids with rheological characteristics have not been discussed in past.Novelty of present study is to examine micro polar Casson fluid towards a stretching sheet in fluenced by internal heat generation.Recent research is a fresh contribution in this regard.Effects of sundry parameters on flow and heat transfer characteristics are examined and discussed in a physical manner.

2 Mathematical Formulation

Consider steady 2D flow of an incompressible micropolar Casson fluid towards a linear stretching convective sheet.Heat and mass transfer flow due to stretching of a heated or cooled surface of variable temperatureT(x)and uniform ambient temperature isT∞(T＞T∞)is considered.The governing equations of motion(i.e.the continuity,momentum,energy)in vector form for micropolar fluid with rheological characteristics are as follow:

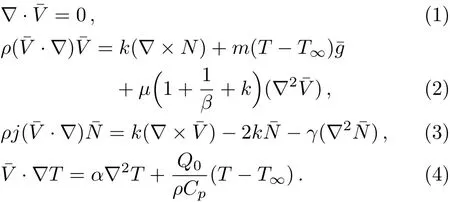
Component form of Eqs.(1)–(4)under boundary layer approximations and considering buoyancy effects are given by:

with appropriate boundary conditions

where in above equationsuandvare velocity components along coordinates axes,uw(x)is velocity at wall,a＞0 is stretching parameter,ρis fluid density,νis kinematic viscosity,kis vortex viscosity,is Casson fluid parameter,Nis micropolar rotation velocity,nis boundary concentration parameter of fluid,the casen=0 represents strong concentration,n=0.5 indicates weak concentration,Cpis the speci fic heat at constant pressurep,κis thermal conductivity of the medium andTis fluid temperature.A stream of cold fluid at temperatureT∞is moving over sheet while the surface of sheet is heated from below by convection from hot fluid at temperatureTfwhich provides a heat transfer coeきcienthf,g0is acceleration due to gravity,mis coeきcient of thermal expansion,Q0is heat generation coeきcient,γis spin radiation viscosity defined asγ=(µ+k/2)jwherej=ν/ais the micro-inertia density.

To convert above system of partial differential equations,we introduce following similarity transformations[32]

Equation(5)is automatically satis fied and Eqs.(6)–(8)become

and corresponding boundary conditions in Eqs.(9)and(10)take the form

whereKis micropolar parameter,λis thermal convective parameter,Pris the Prandtl number,δis heat generation parameter andBiis Biot number which are defined as:

whereGris Grashof number andRexis Reynold number are given by the relations

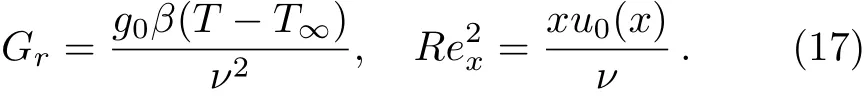
The physical quantities of interest are skin friction coeきcientCfand local Nusselt numberNuxwhich are defined as

where the wall frictionτwand heat transfer at wallqw,are expressed as

In view of Eq.(19),expressions described in(18)provide the skin friction and local Nusselt number as

in whichRex=ax/νis local Reynolds number.

3 The Numerical Solutions

Shooting method along with Runge Kutta fifth order technique was incorporated to tackle the system of nonlinear differential equations.Thus,solution of coupled nonlinear governing boundary layer Eqs.(12)–(14)together with boundary conditions in Eq.(15)are computed by means of shooting method along Runge Kutta fifth order technique.Initially higher order nonlinear differential equations(12)–(14)are converted into a system of first order differential equations and further transformed into initial value problem by labeling the variables as

Associated boundary conditions in Eq.(15)can be transformed as

Above nonlinear coupled ODEs along with initial conditions are solved using Runge Kutta method of order 5 integration techique.Appropriate values of unknown initial conditionsS1,S2andS3are approximated through Newton’s method.Computations are carried out using mathematics softwareMATLAB.End of boundary layer region i.e.,whenη→ ∞ to each group of parameters,is determined when the values of unknown boundary conditions aty=1 do not change to a successful loop with error less than 10−6(see Refs.[33–34]).

4 Results and Discussion

This section is dedicated to examine the in fluence of sundry parameters on velocityf′(η),microrotationg(η)and temperature pro fileθ(η)in the presence of strong(n=0)and weak(n=0.5)concentrations.Figure 1 is plotted to discover in fluence of micropolar parameterKon velocity pro filef′(η)for the case of weak concentration.It can be observed that velocity pro filef′(η)as well as corresponding momentum boundary layer thickness rises with the increasing behavior of micropolar parameterKfor weak concentration.Figure 2 depicts that microrotation pro fileg(η)increases with micropolar parameterKnear the wall for both cases of concentration but reverse behavior is observed away from surface.Figure 3 depicts the in fluence of mixed convection parameterλon microrotation pro fileg(η)for strong as well as weak concentrations is positive.In fluence of Casson fluid parameterβon microrotation pro fileg(η)is presented through Fig.4.It is quite evident that microrotation pro fileg(η)is higher for the case of weak concentration(n=0.5)as compared to strong concentration(n=0).The graph for various values of Biot numberBifor temperature pro fileθ(η)is displayed in Fig.5.It can be seen that temperature increases with attractive conduct of Biot numberBi.Figure 6 is plotted to examine the effect ofδon temperature profileθ(η)for weak concentrationn=0.5.Here a grow in temperature and thermal boundary layer thickness is observed for mount inδfor weak concentrationn=0.5.

Fig.1 Behavior of velocity pro file f′(η)against K.

Fig.2 Behavior of microrotation pro file g(η)against K.

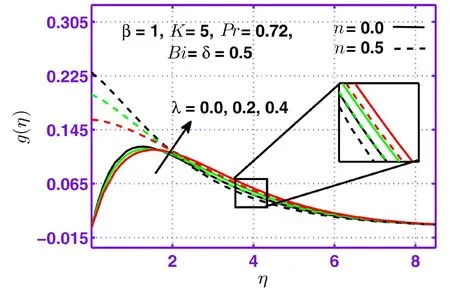
Fig.3 Behavior of microrotation pro file g(η)against λ.

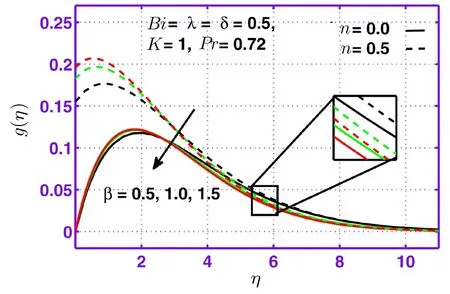
Fig.4 Behavior of microrotaion pro file aganist β for n=0 and n=0.5.

Fig.5 Behavior of temperature pro file θ(η)against Biot number Bi.

Fig.6 Behavior of temperature pro file θ(η)against δ.

To investigate effects of parameters on skin friction coeきcient(−f′′(0))and local Nusselt number(−θ′(0))we have demonstrated Figs.7–10.From Fig.7 it is illustrated that skin friction lessens by rising fluid parameterβfor strong as well as weak concentrations.The behavior of micropolar parameterKon skin friction is seen in Fig.8.It explains that skin friction is a decreasing function ofβas micropolar parameterKincreases.Moreover,Fig.9 demonstrates the effect of micropolar parameterKon Nusselt number(−θ′(0))when plotted against fluid parameterβ.Heat flux(−θ′(0))for weak(n=0.5)and strong(n=0.0)concentrations is displayed in Fig.10.It is observed that heat flux(−θ′(0))as a function of micropolar parameterKfalls with growing values of fluid parameterβ.Effects for concerning parameters have similar behavior as in skin friction for both cases of concentration.

5 Concluding Remarks

The aim of this study is to investigate microrotation effects on mixed convective flow of a Casson fluid induced by a stretching sheet.The governing physical problem is tackled numerically using Runge Kutta Fehlberg scheme coupled with shooting.The core outcomes of this study are:

• The velocity pro filef′(η)and microrotation pro fileg(η)depict opposite behavior against micropolar parameterK.

• Microrotation pro fileg(η)rises with mixed convec

tive parameterλwhile it decreases with Casson fluid parameterβfor strong as well as weak concentration.

• Skin friction coeきcient −f′′(0)and local Nusselt number −θ′(0)rise with micropolar parameterKwhile decrease with Casson fluid parameterβ.

• Higher skin friction coeきcient −f′′(0)and local Nusselt number −θ′(0)are observed for the case of strong concentration(n=0)compared to weak concentration(n=0.5).

Fig.7 Behavior of skin friction coeきcient aganist K for different values of β.

Fig.8 Behavior of skin friction coeきcient aganist β for different values of K.

Fig.9 Behavior of Nusselt number aganist K for different values of β.

Fig.10 Behavior of skin friction coeきcient aganist β for different values of K.

[1]A.C.Eringen,Int.J.Engg.Sci.2(1964)205.

[2]A.C.Eringen,J.Math.Mech.16(1966)1.

[3]T.Ariman,M.A.Turk,and N.D.Sylvester,Int.J.Engg.Sci.11(1973)905.

[4]T.Ariman,M.A.Turk,and N.D.Sylvester,Int.J.Engg.Sci.12(1974)273.

[5]M.M.Khonsari and D.E.Brewe,Acta Mech.105(1994)57.

[6]R.Mehmood,S.Nadeem,and S.Masood,J.Magn.Magn.Mat.401(2016)1006.

[7]R.Nazar,N.Amin,D.Filip,and I.Pop,Int.J.Nonlinear Mech.39(2004)1227.

[8]R.Ellahi and M.Hameed,Int.J.Num.Meth.Heat Fluid Flow 22(2012)24.

[9]O.D.Makinde,T.Chinyoka,and L.Rundora,Comp.Math.Appl.62(2011)3343.

[10]N.Casson,Rheology of Disperse Systems in Flow Equation for Pigment Oil Suspensions of the Printing Ink Type,Rheology of disperse systems,C.C.Mill,Ed.,84–102,Pergamon Press,London,U.K.(1959).

[11]S.A.Shahzad,T.Hayat,M.Qasim,and S.Asghar,J.Chem.Engg.30(2013)187.

[12]S.Nadeem,R.Mehmood,and N.S.Akbar,Int.J.Thermal Sci.78(2014)90.

[13]M.Mustafa,T.Hayat,I.Pop,and A.Aziz,Heat Transf.–Asian Res.40(2011)563.

[14]K.Bhattacharyya,T.Hayat,and A.Alsaedi,Chin.Phys.B 22(2013)024702.

[15]C.H.Chen,J.Heat Mass Transf.33(1998)471.

[16]M.E.Ali and F.Al-Yousef,Int.J.Heat Mass Transf.45(2002)4241.

[17]A.Ishak,R.Nazar,and I.Pop,Meccanica 41(2006)509.

[18]S.Shateyi,S.S.Motsa,and P.Sibanda,Math.Prob.Eng.2010(2010)1.

[19]K.Vajravelu and A.Hadjinicolaou,Int.Commun.Heat Mass Transfer 20(1993)417.

[20]C.H.Chen,Int.J.Non-Linear Mech.44(2009)596.

[21]M.M.Rashidi and S.Abbasbandy,Commun.Nonlin.Sci.Num.Simul.16(2011)1874.

[22]N.T.M.Eldabe and M.G.E.Salwa,J.Phys.Soc.Jpn.64(1995)41.

[23]S.Nadeem,R.Mehmood,and N.S.Akbar,J.Comput.Theor.Nano Sci.11(2014)1422.

[24]I.Pop and D.B.Ingham,Convective heat transfer.Mathematical and computational modeling of viscous fluids and porous media pergamon,Oxford,(2001).

[25]O.D.Makinde,Int.J.Phys.Sci.5(2010)700.

[26]A.Ishak,Appl.Math.Comput.217(2010)837.

[27]O.D.Makinde and P.O.Olanrewaju,Trans.ASME J.Fluid Eng.132(2010)044502.

[28]M.M.Nandeppanavar,K.Vajravelu,M.Subhas Abel,and M.N.Siddalingappa,Meccanica 48(2013)1451.

[29]T.F.Lin,C.J.Chang,and W.M.Yan,J.Heat Transf.110(1988)337.

[30]M.V.Karwe and Y.Jaluria,Int.J.Heat Mass Transfer 35(1992)493.

[31]N.A.Yacob,A.Ishak,I.Pop,and K.Vajravelu,Nanoscale Research Lett.6(2011)1.

[32]M.Qasim,I.Khan,and S.Sha fie,Plos ONE 8(2013)49045.

[33]Z.Mehmood and Z.Iqbal,J.Mol.Liq.224(2016)1083.

[34]E.Azhar,Z.Iqbal,and E.N.Maraj,Zeitschrift fr Naturforschung A 71(2016)837848.