Quantum Phases of Cold Bosonic Atoms in an Optical Lattice with Inhomogeneous Atomic Interactions and Coexistence of Multi Phases∗
Yan-Ying Li(李艳英)and Jing-Min Hou(侯净敏)
Department of Physics,Southeast University,Nanjing 211189,China
In recent decades,cold atoms in optical lattices have become one of the most popular branch of cold atomic physics.[1]Optical lattices can be generated by a set of coherent laser beams and form periodic potentials with de finite geometry structures.The lattice constant,symmetry,potential well depth,and geometric structure of optical lattices can be precisely adjusted by the laser configurations and parameters.The strength of interactions between atoms can be tuned through Feshbach resonance technique.[2]As a result,cold atoms in optical lattice have remarkable advantages compared with solid systems.Therefore,cold atoms in optical lattices are extensively applied to stimulate many physical phenomenons of condensed matter physics and quantum mechanics.
Cold atoms in optical lattices have an important application to stimulate strongly correlated systems,which was begun from the seminal 1998 paper of Jakschet al. on the super fluid-Mott insulator transition.[3]The super fluid-Mott-insulator transition in optical lattices was firstly realized in experiments by Greineret al. in 2002.[4]Since then,many theoretical and experimental studies on quantum phase transition in optical lattices have been appearing.Quantum phases of cold bosinic atoms with dipolar interactions in optical lattices have been studied.[5−6]The super fluid-Mott insulator transition and complex phases have been investigated for undoped and doped two-species cold atoms in optical lattices,respectively.[7−8]The super fluid-Mott insulator transition of spin-2 cold bosons in optical lattice have been studied.[9−10]Novel quantum phases of cold bosons in a superlattice have also been investigated.[11]Quantum phases of Bose–Fermi mixture in three-dimensional lattices have been observed.[12−13]Quantum phases of spinless bosons,two species of bosons and spin-1 bosons in optical lattices with harmonic traps has been discussed.[14]Very recently,the probe technique with single-site resolution was developed to detect the quantum phases of bosons or fermions in optical lattices.[15−19]
In this paper,we study quantum phases of cold bosonic atoms on a square optical lattice with inhomogeneous repulsive atomic interactions,which can be tuned through Feshbach resonance[2]by an inhomogeneous magnetic field.With the tight-binding approximation,we obtain the extended Bose–Hubbard Hamiltonian.Base on the mean- field approximation,we solve the ground states for the extended Bose–Hubbard model by the iterative method.Further,we calculate the average number of particles at each site,i.e.,the particle number density,and the mean- field order parameter,i.e.,the super fluid order parameter.We analyze the distribution of quantum phases based on the particle number density and super fluid order parameter and discuss the quantum phases from the aspect of competitions among the atomic interaction,hopping energy,and the chemical potential.
We consider a system of cold bosonic atoms with site-dependent repulsive interaction in a two-dimensional square optical lattice.The system can be described by a second-quantized Hamiltonian as

wheremis the mass of bosonic atom;r is the coordinate position;†(r)and(r)are the creation and annihilation operators that satisfy the Bose communication rule[(r),†(r)]=δ(r−r′);Vop(r)is the optical latticepotential;µis the chemical potential;g(r)is a positiondependent interaction strength parameter,which can be expressed in terms of the s-wave scattering length asg(r)=4πa(r)ħ2/m,wherea(r)is a position-dependent s-wave scattering length,which can be achieved via the technique of Feshbach resonance.[2]
In order to obtain the tight-binding Hamiltonian,we take Wannier functionsw(r−ri)as the basis.In the lowest band approximation,we express the creation field operator as

Substituting Eq.(2)into Eq.(1),we arrive at the extended Bose–Hubbard Hamiltonian
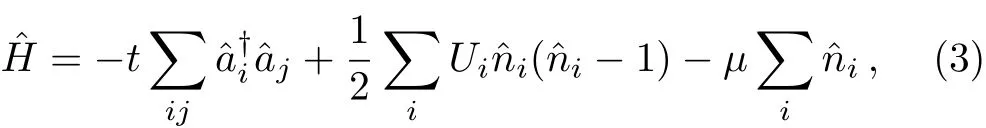

represents the hopping matrix element among adjacent lattice sites;Ui=∫d2rg(r)|w(ri)|4is the site-dependent repulsive interaction energy between two atoms on the same site;since the on-site energy

is the same for all lattice sites,it has been absorbed into the chemical potential term.
With the mean- field approximation,[20]the hopping terms in Eq.(3)can be rewrited as
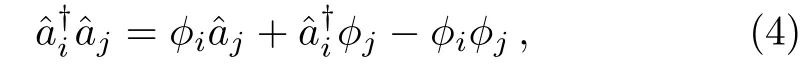
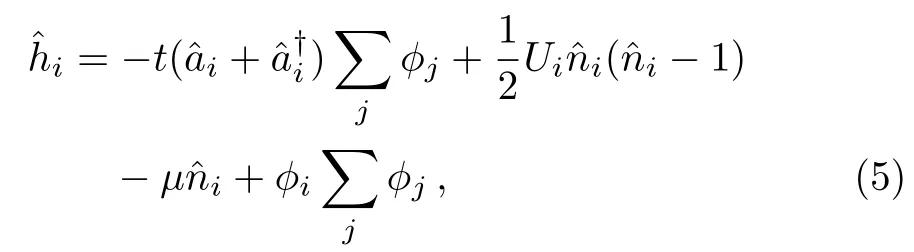
which is the single-site Hamiltonian for an arbitrary lattice sitei,whose is site-diagonal for creation,annihilation,and particle number operators.The neighbor lattice sites are coupled only through the super fluid order parameters.
In this study,we consider that the site-dependent atomic interaction has the form
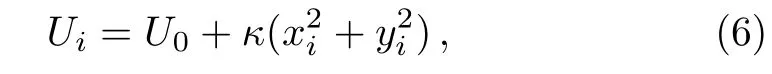
where(xi,yi)is the coordinate of lattice sites andκis a parameter related with the varying rate of atomic interactions with the coordinate.For convenience,we suppose that the lattice constant of the optical lattice is 1 in our study.In experiments,such atomic interaction can be tuned by Feshbach resonance.[2]Here,we apply the iterative method to solve the ground state of the coupled single Hamiltonians as Eq.(5).We consider a finite lattice with 101×101 lattice sites and set the cut-offparticle number of each site as 8 in the process of calculation.The chemical potential is set asµ=150tand the parametersU0andκare set asU0=60tandκ=0.05tfor the concrete calculation.From the ground state,we evaluate the particle number density and the super fluid order parameter,which are shown in Fig.1(a)and Fig.1(b),respectively.

Fig.1 (Color online)(a)The distribution of the average particle number density and(b)the distribution of the super fluid order parameter for cold bosonic atoms in a square optical lattice with inhomogeneous repulsive interactions.The values of the dimensionless parameters(κ/t,U0/t,µ/t)are(0.05,60,150).
From the results,we find that the Mott insulator and super fluid phases coexist in the lattice.Mott insulator is characterized by integer particle number at each site and vanishing mean- field parameter,i.e.,ϕ=0.Superfluid phase is a coherent state,so it has a non-vanishing mean- field order parameter,i.e.,the super fluid order parameter and a non-integer particle number density.Figure 1(a)shows that there exist three plateaus with particle number densityn=3,2,1 from the center to the edge of the lattice and there also exist non-integer particle number density between two plateaus.Thus,we can conclude that Mott insulator and super fluid phases coexist in the lattice.From the center to the edge,they are Mott insulator withn=3,super fluid phase with 2<n<3,Mott insulator withn=2,super fluid phase with 1<n<2,and Mott insulator withn=1 in sequence.To con firm our conclusion,we verify the mean- field order parameter diagram shown in Fig.1(b).From Fig.1(b),we see that,there are two annuluses having non-vanishing mean- field order parameter,which indicates that the super fluid phase appears there.On the other areas,the mean- field order parameter vanishes,which indicates the existence of Mott insulators.From the center to the edge,they correspond to the Mott insulators withn=3,2,1,respectively.The analysis from the mean- field order parameter is consistent with the results concluded from the particle number density.
We can interpret the results from the competitions among the atomic interaction,the hopping energy,and the chemical potential,which determines the appearance of phases.At the origin of the lattice,the atomic interaction strength isU=60t.For the chemical potentialµ=150tas set for the calculation,near the origin of the lattice,the Mott insulator with exact 3 atoms at a lattice site has a less energy than a coherent state with average 3 atoms at a lattice site.Therefore,on the central area,the Mott insulator withn=3 appears.The atomic interaction increases according to Eq.(6)when the position varies from the origin to the edge.The radius of the central disc is approximately 10 times of lattice constant.At the boundary of the central disc,the atomic interaction is approximatelyU≃65t.With such parameters,the atomic interaction energy increases to a critical value that can not be compensated the chemical potential term,which makes the avarage number of atoms at lattice sites decrease to less than 3.Furthermore,the atomic hopping between lattice sites further lower the total energy.Therefore,the mean- field order parameter becomes non-zero,which indicates the appearance of the superfluid phase.When the distance from the origin arrives at approximately 22 times of lattice constant,the atomic interaction strength increases toU≃84t,which is a critical point between the sup fluid phase and the Mott insulator withn=2.Beyond this critical point,the gain of energy due to increase of atomic interaction can not be compensated by the hopping energy,so Mott insulator withn=2 appears.When the radius reaches 39 times of lattice constant,the atomic interaction strength isU≃136t.Beyond this critical point,the increase of the atomic interaction energy can not be compensated by the chemical potential terms,which makes the particle number density decrease to less than 2.The hopping energy further lower the total energy and the phase tends to a coherent phase with 1<n<2,i.e.,a super fluid phase.When the radius reaches 46 times of lattice constant,the atomic interaction strength isU≃166t.Beyond this critical point,the hopping energy can not compensate the atomic interaction energy forn≥2,so the Mott insulator withn=1 appears.
In experiments,microscopic measurements single-site resolution in optical lattices were realized for bosonic systems and have been used to study ordering,spatial structures,and correlations in the Bose–Hubbard model.[15−18]Very recently,such single-site probe technique was also developed for fermionic atoms.[19]Therefore,such techniques can be used to probe coexistence of the Mott insulator and the super fluid phase predicted in our study.
In summary,we have studied cold bosonic atoms on a square optical lattice with inhomogeneous atomic interactions.With the tight-binding approximation,the system is described by an extended Bose–Hubbard Hamiltonian.We simpli fied the extended Bose–Hubbard Hamiltonian into a series of single-site Hamiltonians by the mean- field method. The single-site Hamiltonians of the neighbor lattice sites are coupled by the mean- field order parameters.We iteratively solved the ground state of the coupled single-site Hamiltonians.We also calculated the average particle number at each site and the mean- field order parameter and found that the Mott-insulator phase and the super fluid phase coexist on the same optical lattice.For the case with the chemical potentialµ=150t,there exist the Mott insulator withn=3,the super fluid phase with 2<n<3,the Mott insulator withn=2,the super fluid phase with 1<n<2,and the Mott insulator withn=1 in sequence from the center to edge.We have analyzed the results from the aspect of the competitions among the atomic interaction,the hopping energy,and the chemical potential.
[1]M.Lewenstein,A.Sanpera,V.Ahu finger,B.Damski,A.Sen,and U.Sen,Adv.Phys.56(2007)243.
[2]E.Timmermans,P.Tommasini,M.Hussein,and A.Kerman,Phys.Rep.315(1999)199.
[3]D.Jaksch,C.Bruder,J.I.Cirac,C.W.Gardiner,and P.Zoller,Phys.Rev.Lett.81(1998)3108.
[4]M.Greiner,O.Mandel,T.Esslinger,T.W.Hänsch,and I.Bloch,Nature(London)415(2002)39.
[5]K.G´oral,L.Santos,and M.Lewenstein,Phys.Rev.Lett.88(2002)170406.
[6]A.L.Gadsbølle and G.M.Bruun,Phys.Rev.A 85(2012)021604.
[7]A.Isacsson,M.C.Cha,K.Sengupta,and S.M.Girvin,Phys.Rev.B 72(2005)184507.
[8]K.Hettiarachchilage,V.G.Rousseau,K.M.Tam,M.Jarrell,and J.Moreno,Phys.Rev.B 88(2013)161101.
[9]J.M.Hou and M.L.Ge,Phys.Rev.A 67(2003)063607.
[10]S.Jin,J.M.Hou,B.H.Xie,L.J.Tian,and M.L.Ge,Phys.Rev.A 70(2004)023605.
[11]J.M.Hou,Mod.Phys.Lett.B 23(2009)25.
[12]S.Ospelkaus,C.Ospelkaus,O.Wille,M.Succo,P.Ernst,K.Sengstock,and K.Bongs,Phys.Rev.Lett.96(2006)180403.
[13]K.Günter,T.Stöferle,H.Moritz,M.Köhl,and T.Esslinger,Phys.Rev.Lett.96(2006)180402.
[14]R.V.Pai,J.M.Kurdestany,K.Sheshadri,and R.Pandit,Phys.Rev.B 85(2012)214524.
[15]W.S.Bakr,A.Peng,M.E.Tai,R.Ma,J.Simon,J.I.Gillen,S.Fölling,L.Pollet,and M.Greiner,Science 329(2010)547.
[16]J.F.Sherson,C.Weitenberg,M.Endres,M.Cheneau,I.Bloch,and S.Kuhr,Nature(London)467(2010)68.
[17]M.Endres,M.Cheneau,T.Fukuhara,et al.,Science 334(2011)200.
[18]M.Cheneau,P.Barmettler,D.Poletti,M.Endres,P.Schauß,T.Fukuhara,C.Gross,I.Bloch,C.Kollath,and S.Kuhr,Nature(London)481(2012)484.
[19]L.W.Cheuk,M.A.Nichols,K.R.Lawrence,M.Okan,H.Zhang,and M.W.Zwierlein,Phys.Rev.Lett.116(2016)235301.
[20]D.Van Oosten,P.Van der Straten,and H.T.C.Stoof,Phys.Rev.A 63(2001)053601.
 Communications in Theoretical Physics2017年4期
Communications in Theoretical Physics2017年4期
- Communications in Theoretical Physics的其它文章
- Dynamics of Optical Bistability with Kerr-nonlinear Blackbody Radiation Reservoir
- Higgs and Single Top Associated Production at the LHC in the Left-Right Twin Higgs Model∗
- Special Property of Group Velocity for Temporal Dark Soliton∗
- Collisions and Trapping of Time Delayed Solitons in Optical Waveguides with Orthogonally Polarized Modes∗
- Dual Solutions of MHD Boundary Layer Flow of a Micropolar Fluid with Weak Concentration over a Stretching/Shrinking Sheet
- Instability Analysis of Positron-Acoustic Waves in a Magnetized Multi-Species Plasma
