Special Property of Group Velocity for Temporal Dark Soliton∗

Ying-Jie Du(杜英杰),Jin-Ying Yu(于金影),and Jin-Tao Bai(白晋涛),2,†School of Physics,Northwest University,Xi’an 70069,China

2Institute of Photonics and Photon-technology,Northwest University,Xi’an 710069,China

Since human discovered the electromagnetical nature of light,it has been found that the velocity of light is related to the optical effects of the medium.It is well known that the velocity of light is determined by the refractive index of the medium.With deepening of the research,human found that the velocity of light also depends on the dispersive effect of medium.We refer to the former as the phase velocity,while the latter is referred to as the group velocity,which is used to describe the propagation of optical pulses.On the basis of the degree of dispersion,researchers anticipate to manage the velocity for the interest of all-optical devices.[1−3]Recent years a number of efforts have been devoted on the slowdown of light based on steep dispersive effect.[4−12]Due to the steep dispersion with a trivial absorption,the optical media involving quantum coherence[13−14]attracted a lot of attentions.Hauet al.observed the spectacular reduction of the group velocity to 17 m/s in a Bose condensate of Na atoms.[8]Phillipset al.decelerated and trapped a light pulse in a vapor of Rb atoms.[12]Additionally,this medium has signi ficant Kerr nonlinearity,which gives rise to another interests for the generation of nonlinear wave like solitons.Recently,researchers have investigated nonlinear waves in this medium,and slow-light bright and dark soliton,[15−16]fast-light soliton[17]as well as other solitons[18−19]have been investigated.

Dark solitons[20−23]are one or more dips in nonzero optical background that are capable of preserving their intensities and widths over a long-distance propagation.In the nonlinear Schrödinger equation(NLSE)the existence of dark solitons depends on the same signs of dispersion or diffraction and Kerr nonlinearity.The formation of dark solitons relies on the balance of competition between linear and nonlinear effects.Unique features of dark soliton arouse a lot of interests.It is known that the phase of bright solitons is constant across the entire pulse,while in contrast the phase of the dark soliton keeps changing across the entire dark soliton pulse.[24]For the velocity of the temporal solitons,the bright one is related to the linear effect of the medium like dispersion.The unique structure of dark soliton makes the group velocity quite different from the bright soliton.However,there is rare work has been done on the issue of the group velocity of dark soliton,especially in coherent optical medium where slow-light bright soliton is present.

In this paper we investigate the group velocity of temporal dark soliton in a coherent optical medium.The motion equations of density matrix elements decide the linear and nonlinear responses of lights to atoms.We describe the evolution of optical field by a nonlinear partialdifferential equation whose coeきcients are related to those responses.On appropriate parameters the described equation changes into the NLSE.Based on the solutions of dark solitons of the NLSE,we investigate the group velocity of dark solitons.It is shown that the group velocity not only relies on the linear parameters of the mediumbut also relies on the nonlinear parameter of the medium.The velocity in normal and anomalous dispersions are also different.

We consider a medium comprised by the atoms with Λ-type con figuration,as shown in Fig.1.In the atomic system the levels|2〉and|3〉are hyper fine lower energy levels,and|1〉is an excited energy level.A continuouswave(cw)coupling field with frequencyωCcouples the transition|3〉→ |1〉with the Rabi frequency 2ΩCin a detuning ΔC.Another dark pulse with the carrier frequencyωPdrives the transition|2〉→ |1〉with the Rabi frequency 2ΩPand the detuning ΔP.γ12,γ13andγ23are the decay rates in the transition|1〉→ |2〉,|1〉→ |3〉,and|2〉→ |3〉,respectively.

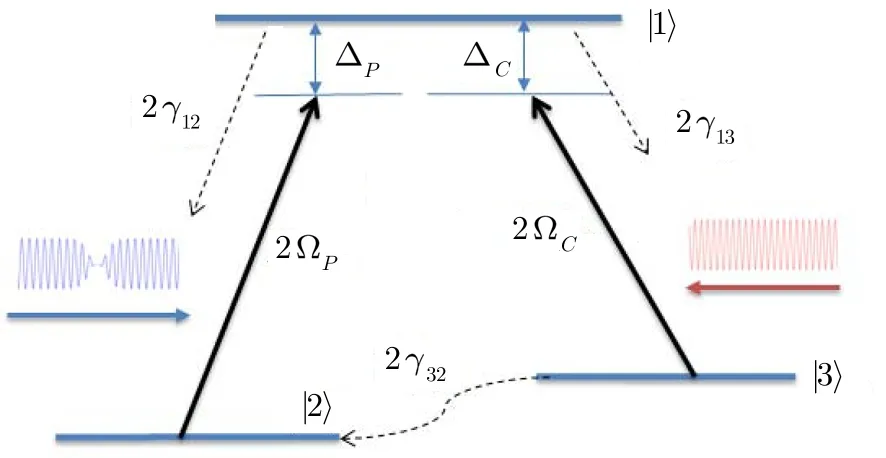
Fig.1 Energy-level diagram of atomic system.The transition |2〉 → |1〉isdriven by adark-pulsed continuous-wave(cw)probe field with the Rabi frequency 2ΩP,and meanwhile the transition|3〉→ |1〉is coupled by a cw coupling field with the Rabi frequency 2ΩC.ΔP and ΔCare the detunings of the two light fields,respectively.γij,(i,j=1,2,3),are the decay rates for the transitions|i〉→ |j〉.

Under interaction picture,the Hamiltonian of the light-atoms interaction system in the approximations of dipole and rotating wave can be written as

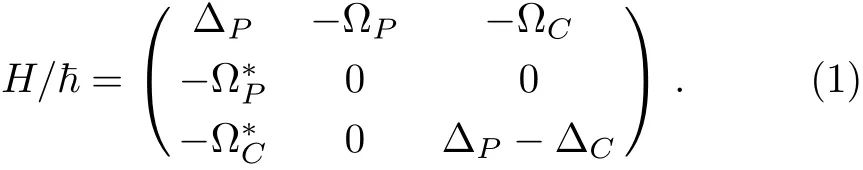
The evolution of the quantum state of the system is governed by the Master equation

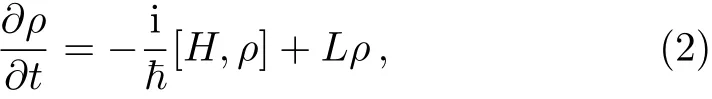
where the termLρresponsible for decay is defined by

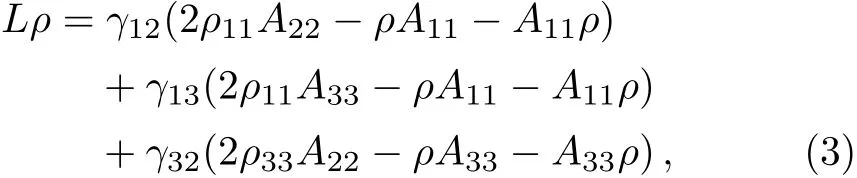
whereAijis defined byAij=|i〉〈j|.The evolution equations for density matrix elements are then given by

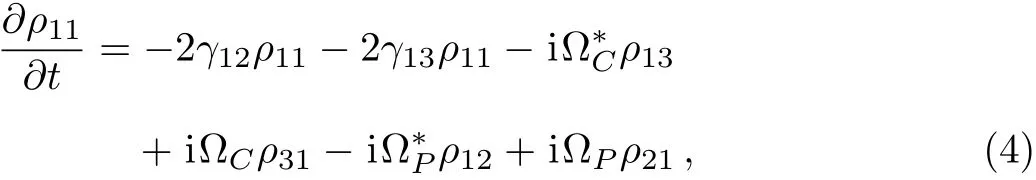
whereγ=γ12+γ13+γ32,γ′=γ12+γ13withγij,(i,j=1,2,3)being the decay rates for the transitions|i〉→ |j〉.

To describe the behavior of the probe field,the Maxwell equations must be applied.However,attaining the propagation equation,some assumptions or restrictions must be applied.We limit the polarization of the probe field maintained along the medium,and assume the optical field to be quasi-monochromatic.Using the scalar approach and separating the rapidly varying part of the electric field,the Maxwell equations in the present optical medium reduce to the wave equation

whereEis the slowly varying amplitude of the probe electric field,andPLandPNLare the slowly varying amplitude of the linear and nonlinear electric polarizations.To obtain the wave equation for the slowly varying amplitudeE,it is quite convenient to work in the Fourier domain.With the Fourier transform in terms ofE

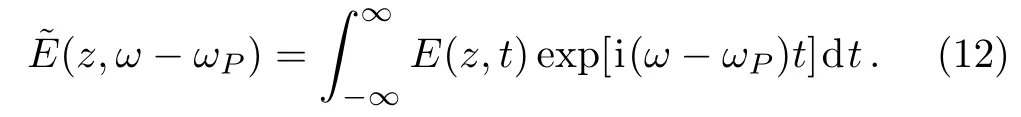
Equation(11)changes into a Helmholtz equation in the form

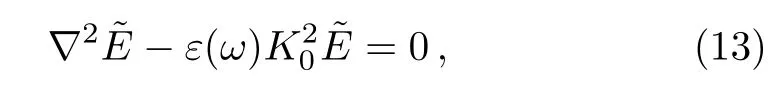
wherek0=ωP/candε(ω)=1+χ(1)+εNL,whereεNLdefined byεNL=(3/4)χ(3)|E(z,t)|2.By using the method of separation of variables

whereF(x,y)is the transverse distribution of the probe field,A(z,ω)is a slowly varying f unction ofz,andβ0is a wave number to be determined later,Equation(13)becomes[18]

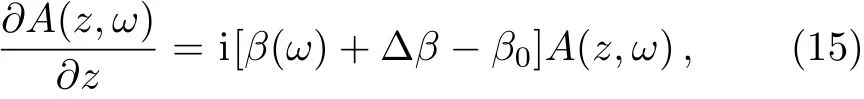
whereβ0and Δβare defined byβ0=β(ωP)and Δβ=k0n2withn2=(3/8)χ(3)/n,respectively.It is useful to deal withβ(ω)in the Taylor transformation

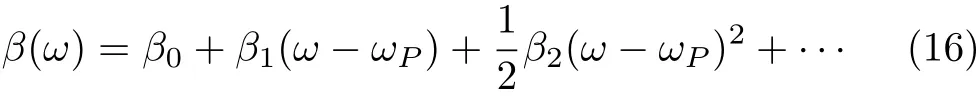
In Eq.(16)βm=(dmβ/dωm)|ω=ωP,m=1,2,3,...The cubic and higher-order terms in this expansion are generally negligible if the spectral width Δω≪ωP.After substituting Eq.(16)in Eq.(15),we replaceω−ωPby the differential operator i∂/∂t.The equation for slowly varying amplitudeA(z,t)can be written as

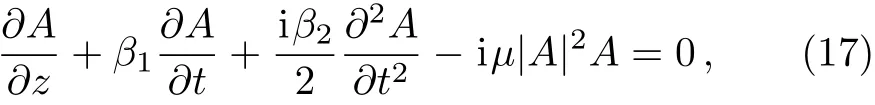
whereβ1andβ2are related to group velocity and group velocity dispersion(GVD),and they are defined by

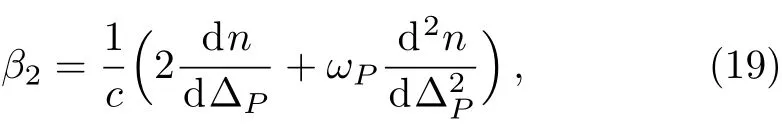
where While the parameterµin Eq.(17)is given byµ=(3/8)k0χ(3)/n.

In the nonlinear equation shown in Eq.(17)the coefficients play an important role in the form of the wave as well as the stability of the wave.One can see that these coeきcients are decided by the first-and third-order susceptibilities of the medium.They can be obtained through the motion equation for density matrix elements.The firstorder and third-order susceptibilities are finally given by

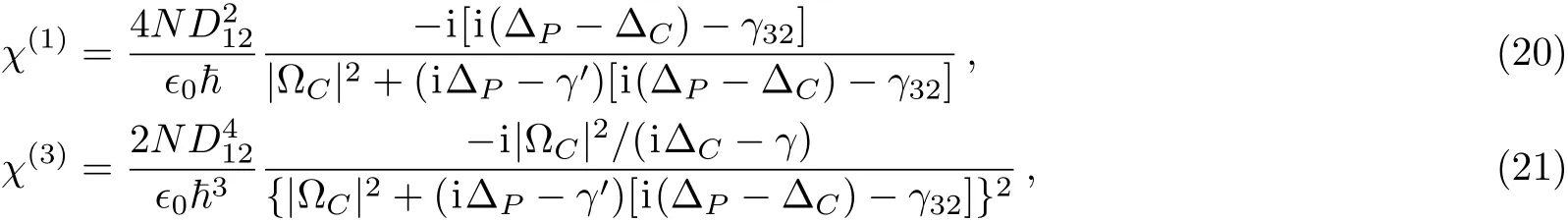
whereD12is the dipole moment of atoms,ϵ0is the dielectric constant in vacuum,ħ is Planck constant,andNis atomic concentration.

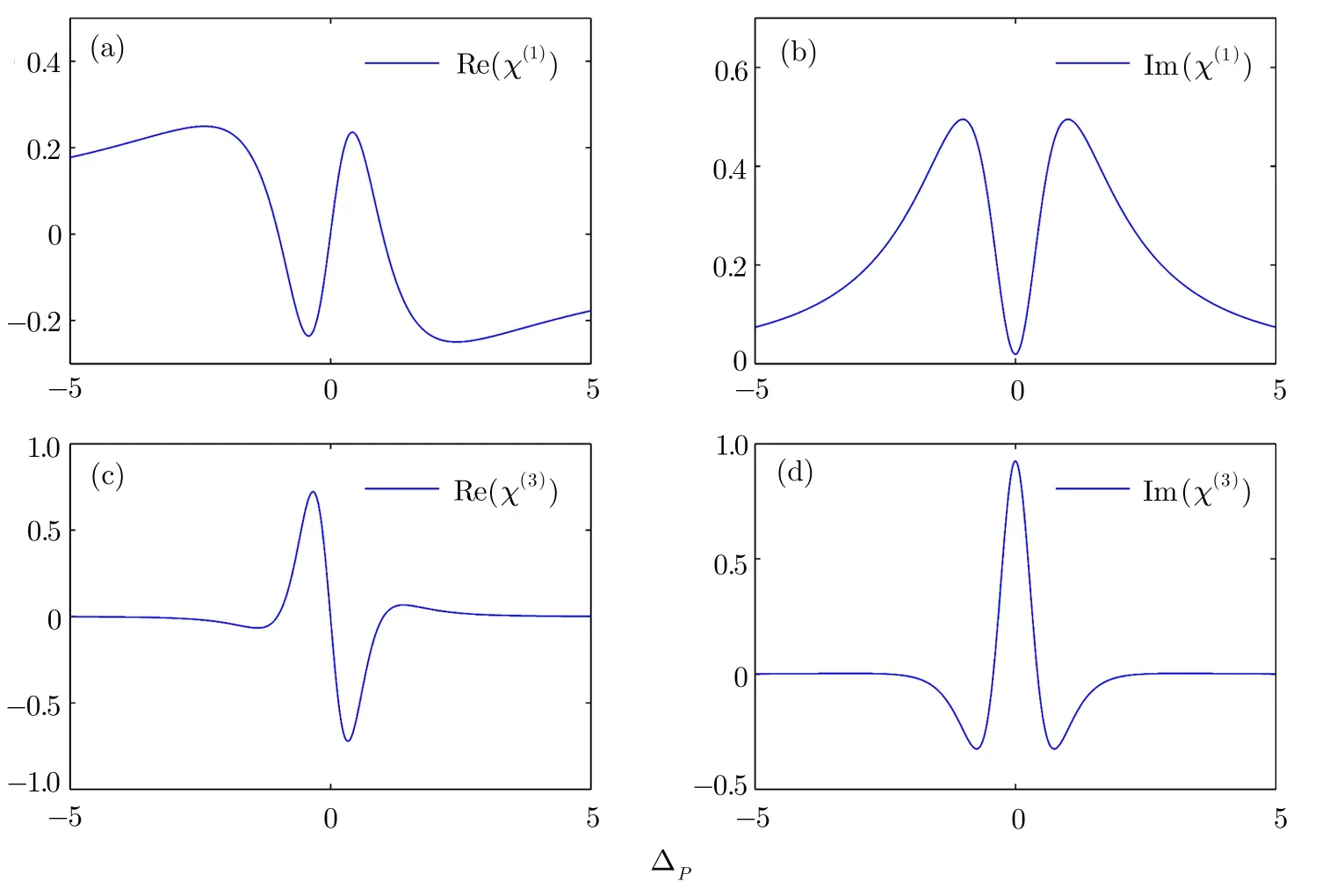
Fig.2 The linear susceptibility(a)and(b)and the nonlinear susceptibilities(c)and(d)as functions of the probe detuning with the parameters γ12=1,γ13=1,γ32=0.01,ΩC=1,and ΔC=0.

Due to the case that the linear and nonlinear susceptibilities(shown in Fig.2)are complex numbers the nonlinear equation(17)is known as the complex Ginzburg–Landau equation.If the imaginary parts of the termsβ2andµare zero the equation will reduce to the NLSE.In Fig.3 one can see that the imaginary parts of the both parameters are simultaneously zero when the probe detuning ΔP= −0.38γ31.In this case the equation(17)can be readily transformed.We use the transformation of variables in the following

whereT0stands for the width of the input pulse whileLDdenotes the dispersion length which has the relationAfter using this set of transformation of variables,the equation(17)becomes a normalized NLSE

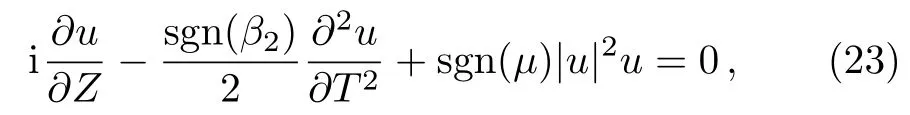
where sgn(β2)and sgn(µ)are the signs of the parametersβ2andµ,respectively.The emerge of the dark soliton depends on the same sign of both real parts of the two parameters.From Fig.3 one can see the both parameters are positive,and it is evident that the case satisfy the condition of the existence of the dark soliton.

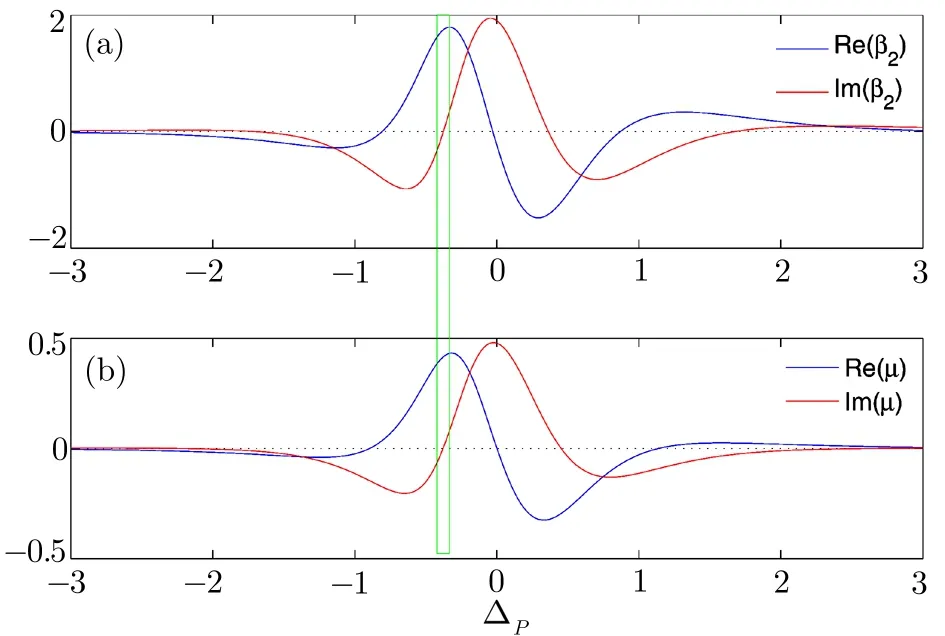
Fig.3 The parameters of β2and µ with the detuning ΔP.(a)the real and imaginary parts of β2(b)the real and imaginary parts ofµunder the parameters being the same to the Fig.2.The constant term 4ND212/ϵ0ħ =1.

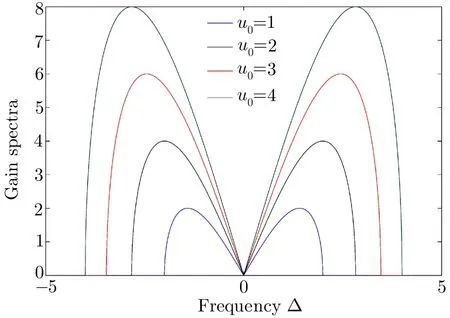
Fig.4 The gain spectra of the perturbation under the same sign of the β2and µ with different initial power.

Fig.5 The group velocity of dark soliton as a function of the parameter of SPM,with(a)normal dispersion(b)anomalous dispersion under the parameters β1=0.01,β2=0.001,and T0=0.01.

However,the same sign of the GVD and self-phase modulation(SPM)gives rise to the instability of the system under a modulation.Figure 4 provides the gain spectra of the perturbation as a modulation under the modulation instability(MI)with different values of the initial power.It shows that the gains achieved not only rely on the detuning of the perturbation but also depend on the initial power of the dark soliton.We write dark soliton solutions in normal and anomalous dispersions asu(T,Z)= Ψ(T,Z)expwhere Ψ(T,Z)is given by

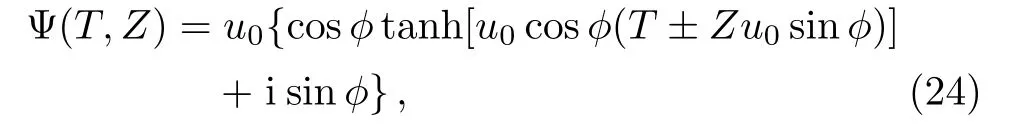
whereu0is the background amplitude of the dark soliton,ϕis an arbitrary angle variable.The magnitude of the dark soliton is governed by the term cos2ϕ.

Fig.6 The group velocity of dark soliton as a function of the parameter of GVD,with(a)normal dispersion(b)anomalous dispersion under the parameters β1=0.1,µ=0.01,and T0=1.

Investigating the group velocity of the dark soliton,we trace the center of the dark soliton which is also the bottom of the dark soliton. After the operation∂|Ψ(T,Z)|/∂T=0,we can write the group velocity of the dark soliton as

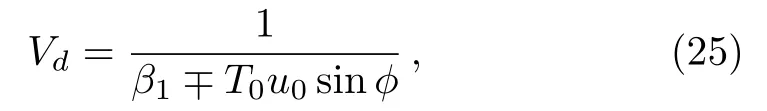
where the sign “−” corresponds to the case of normal dispersion while the sign “+”corresponds to the case of anomalous dispersion.If taking a shape of dark soliton as the initial wave,we can attain the expression of the parameter sinwhereU0is the height of the bottom of the dark soliton,which actually is determined by the grey scale of the dark soliton.With the result the group velocity of the dark soliton can be written as

As a contrast,the group velocity of the general bright soliton is given by It is clear that the speed of the bright soliton only relies on the parameter of group velocity.In the case of the dark soliton,the velocity is not only related to the group velocity parameter but also related to the SPM,GVD and initial amplitude.It needs to note that the velocity depending on the initial power comes from the MI,and this result can be seen in temporal optical breathers.This situation also happens for breathers which originate from MI.In order to investigate the effect of the extra parameters,we plot the speed of dark soliton as functions of the parameters of SPM and GVD.Figure 5 describes the group velocity of the dark soliton varying with the nonlinear parameterµin the normal and anomalous dispersions.It can be seen that it has opposite trend of evolution with the variableµfor the normal and anomalous dispersion.In normal dispersion the speed enhances with the growth of the nonlinear parameter,while the speed reduces with growth of the parameter in anomalous dispersion,and the speed in normal dispersion is larger than that in anomalous dispersion under the same condition.

Apart from the nonlinear parameter of SPM,the parameter of GVD is also related to the speed of dark soliton in another way.Figure 6 shows the speed varies with the parameterβ2in normal and anomalous dispersion.In normal dispersion,under the given parameters it has an odd point in which the rapid variation takes place.In this case a negative speed exists and meantime the superluminal speed of dark soliton also exist.After that the speed reduces to zero with the increase of the parameter GVD.In anomalous dispersion,the speed enhances with the increase of the parameter.This behavior is different with the nonlinear parameter under this dispersion.

In summary,we have investigated the group velocity of dark soliton in a coherent medium.Based on the linear and nonlinear responses,we obtain a Ginzburg–Landau equation which reduces to the NLSE when the imaginary parts of the linear and nonlinear parameters.Based on the solution of dark soliton under the model of the NLSE,we trace the bottom of the dark soliton and obtain the speed of the dark soliton in normal and anomalous dispersions.The research leads to two conclusions,(i)the dark soliton velocity is not only related to the factors of group velocity parameter,but also related to the factors of GVD,SPM parameters as well as the amplitude of dark soliton;(ii)it has different performance for dark soliton in different dispersions that the dark soliton in normal dispersion runs faster than the one in anomalous dispersion.Dark soliton is maybe better than the bright soliton in the control of speed of light.

[1]T.Krauss,Nature Photon 2(2008)448.

[2]L.Thevenaz,Nature Photon 2(2008)474.

[3]T.Baba,Nature Photon 2(2008)465.

[4]A.Kasapi,M.Jain,G.Y.Yin,and S.E.Harris,Phys.Rev.Lett.74(1995)2447.

[5]H.Schmidt and A.Imamoglu,Opt.Lett.21(1996)1936.

[6]M.Xiao,Y.Li,S.Jin,and J.Gea-Banacloche,Phys.Rev.Lett.74(1995)666.

[7]M.D.Lukin,M.Fleischhauer,A.S.Zibrov,et al.,Phys.Rev.Lett.79(1997)2959.

[8]L.V.Hau,S.E.Harris,Z.Dutton,and C.H.Behroozi,Nature(London)397(1999)594.

[9]M.M.Kash,V.A.Sautenkov,A.S.Zibrov,et al.,Phys.Rev.Lett.82(1999)5229.

[10]A.V.Turukhin,V.S.Sudarhanam,M.S.Shahriar,J.A.Musser,B.S.Ham,and P.R.Hemmer,Phys.Rev.Lett.88(2001)023602.

[11]D.F.Philips,A.Fleischhauer,A.Mair,R.L.Walsworth,and M.D.Lukin,Phys.Rev.Lett.86(2001)783.

[12]A.Melloni,F.Morichetti,and M.Marinelli,Opt.Quantum Electron.35(2003)365379.

[13]S.E.Harris,Phys.Today 50(7)(1997)36.

[14]M.Fleischhauer,A.Imamoglu,and J.P.Marangos,Rev.Mod.Phys.77(2009)633.

[15]Y.Wu and L.Deng,Phys.Rev.Lett.93(2004)143904.

[16]S.L.Fan,Y.P.Shi,H.J.Zhang,and H.Sun,Chin.Phys.B 21(2012)114203.

[17]G.Huang,C.Hang,and L.Deng,Phys.Rev.A 77(2008)011803.

[18]Y.Zhang,M.Blic,Z.Wu,C.Yuan,R.Wang,K.Lu,and Y.Zhang,Phys.Rev.A 88(2013)013847.

[19]Y.J.Du,X.T.Xie,J.Y.Yu,and J.T.Bai,Chin.Phys.Lett.32(2015)074210.

[20]A.Hasegawa and F.Tappert,Appl.Phys.Lett.23(1973)142.

[21]Y.S.Kivshar and B.Luther-Davies,Phys.Rep.298(1998)81.

[22]X.H.Gao,C.Y.Zhang,D.Tang,H.Zheng,D.Q.Lu,and W.Hu,Acta Phys.Sin.62(2013)044214(in Chinese).

[23]C.Liu,Z.Y.Yang,M.Zhang,T.Zhang,W.L.Yang,and R.H.Yue,Commun.Theor.Phys.59(2013)703.

[24]Y.S.Kivshar and G.P.Agrawal,Optical Solitons:From Fibers to Photonic Crystals,Academic,San Diego(2003).